思考并回答以下问题:
- 有序数组和普通数组在线性查找方面有什么不同?
- 有序数组还可以使用什么查找方法?为什么普通数组无法使用?
- 有序数组在插入方面和普通数组有什么区别?谁快谁慢?
- 用Python或Ruby代码实现线性查找和二分查找。
本章涵盖:
- 有序数组
- 查找有序数组
- 二分查找
- 二分查找与线性查找
上一章我们学习了两种数据结构,并明白了选择合适的数据结构将会显著地提升代码的性能。即使是像数组和集合这样相似的两种数据结构,在高负荷的运行环境下也会表现得天差地别。
在本章,你将会发现,就算数据结构确定了,代码的速度也还会受另一重要因素影响,那就是算法。
算法这个词听起来很深奥,其实不然。它只是解决某个问题的一套流程。准备一碗麦片的流程也可以说是一种算法,它包含以下4步(对我来说是4步吧)。
(1) 拿个碗。
(2) 把麦片倒进碗里。
(3) 把牛奶倒进碗里。
(4) 把勺子放到碗里。
在计算机的世界里,算法则是指某项操作的过程。上一章我们研究了4种主要操作,包括读取、查找、插入和删除。这一章我们还是会经常提到它们,而且一种操作可能会有不止一种做法。
也就是说,一种操作会有多种算法的实现。我们很快会看到不同的算法能使代码变快或者变慢——高负载时甚至慢到停止工作。不过,现在先来认识一种新的数据结构:有序数组。它的查找算法就不止一种,我们将会学习如何选出正确的那种。
有序数组
有序数组跟上一章讨论的数组几乎一样,唯一区别就是有序数组要求其值总是保持有序(你猜对了)。即每次插入新值时,它会被插入到适当的位置,使整个数组的值仍然按顺序排列。常规的数组则并不考虑是否有序,直接把值加到末尾也没问题。
以数组[3, 17, 80, 202]为例。
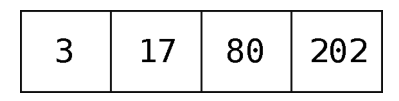
假设这是个常规的数组,你准备将75插入,那就可以把它放到尾端,如下所示。
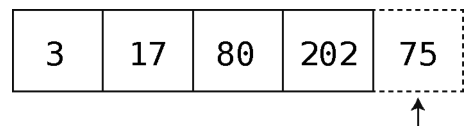
如上一章所述,计算机只要1步就能完成这种操作。
但如果这是一个有序数组,你就必须要找到一个适当的位置,使插入75之后整个数组依然有序。
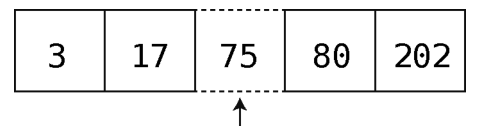
做起来可不像说的那么简单。整个过程不可能一步完成,因为计算机需要先找出那个适当的位置,然后将其及以后的值右移来腾出空间给75。下面就来介绍分解的步骤。
先回顾一下原始的数组。
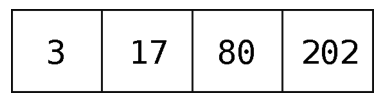
第1步:检查索引0的值,看75应该在它的左边还是右边。
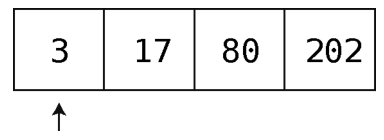
因为75大于3,所以75应该在它右边的某个位置。而具体的位置,目前还是不能确定,于是,再检查下一个格子。
第2步:检查下一格的值。
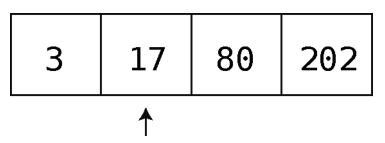
因为75大于17,所以继续。
第3步:检查下一格的值。
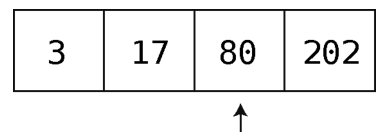
这次是80,大于75。因为这是第一次遇到大于75的值,可想而知,必须把75放在80的左侧以使整个数组维持有序。但要在这里插入75,还得先将它的位置空出来。
第4步:将最后一个值右移。
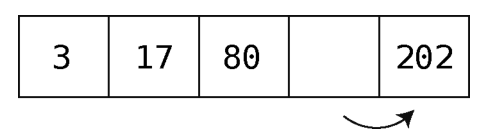
第5步:将倒数第二个值右移。
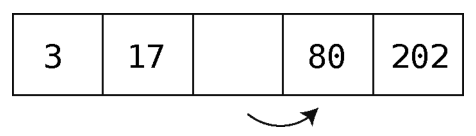
第6步:终于可以把75插入到正确的位置上了。
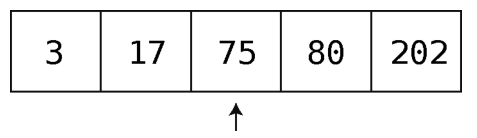
可以看到,往有序数组中插入新值,需要先做一次查找以确定插入的位置。这是它跟常规数组的关键区别(在性能方面)之一。
虽然插入的性能比不上常规数组,但在查找方面,有序数组却有着特殊优势。
查找有序数组
上一章介绍了常规数组的查找方式:从左至右,逐个格子检查,直至找到。这种方式称为线性查找。
接下来看看有序数组的线性查找跟常规数组有何不同。
设一个常规数组[17,3,75,202,80],如果想在里面查找22(其实并不存在),那你就得逐个元素去检查,因为22可能在任何一个位置上。要想在到达末尾之前结束检查,那么所找的值必须在末尾之前出现。
然而对于有序数组来说,即便它不包含要找的值,我们也可以提早停止查找。假设要在有序数组[3,17,75,80,202]里查找22,我们可以在查到75的时候就结束,因为22不可能出现在75的右边。
以下是用Ruby语言实现的有序数组线性查找。1
2
3
4
5
6
7
8
9
10
11
12
13
14def linear_search(array, value)
# 遍历数组的每一个元素
array.each do |element|
# 如果这个元素等于我们要找的值,则将其返回
if element == value
return value
# 如果这个值大于我们要找的值,则提早退出循环
elsif element > value
break
end
end
# 如果没找到,则返回空值
return nil
end
因此,有序数组的线性查找大多数情况下都会快于常规数组。除非要找的值是最后那个,或者比最后的值还大,那就只能一直查到最后了。
只看到这里的话,可能你还是不会觉得两种数组在性能上有什么巨大区别。
这是因为我们还没释放算法的潜能。这是接下来就要做的。
至今我们提到的查找有序数组的方法就只有线性查找。但其实,线性查找只不过是查找算法的其中一种而已。这种逐个格子检查直至找到为止的过程,并不是查找的唯一途径。
有序数组相比常规数组的一大优势就是它可以使用另一种查找算法。此种算法名为二分查找,它比线性查找要快得多。
二分查找
你小时候或许玩过这样一种猜谜游戏(或者现在跟你的小孩玩过):我心里想着一个1到100之间的数字,在你猜出它之前,我会提示你的答案应该大一点还是小一点。
你应该凭直觉就知道这个游戏的策略。一开始你会先猜处于中间的50,而不是1。为什么?
因为不管我接下来告诉你更大或是更小,你都能排除掉一半的错误答案!
如果你说50,然后我提示要再大一点,那么你应该会选75,以排除掉剩余数字的一半。如果在75之后我告诉你要小一点,你就会选62或63。总之,一直都猜中间值,就能不断地缩小一半的范围。
下面来演示这个过程,但仅以1到10为例。
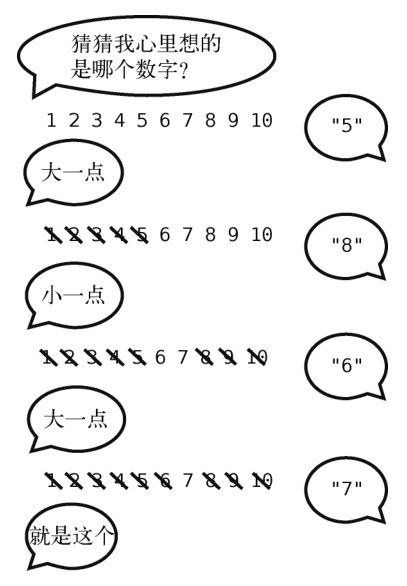
这就是二分查找的通俗描述。
有序数组相比常规数组的一大优势就是它除了可以用线性查找,还可以用二分查找。常规数组因为无序,所以不可能运用二分查找。
为了看出它的实际效果,假设有一个包含9个元素的有序数组。计算机不知道每个格子的值,如下图所示。

然后,用二分查找来找出7,过程如下。
第1步:检查正中间的格子。因为数组的长度是已知的,将长度除以2,我们就可以跳到确切的内存地址上,然后检查其值。

值为9,可推测出7应该在其左边的某个格子里。而且,这下我们也排除了一半的格子,即9右边的那些(以及9本身)。

第2步:检查9左边的那些格子的最中间那个。因为这里最中间有两个,我们就随便挑了左边的。
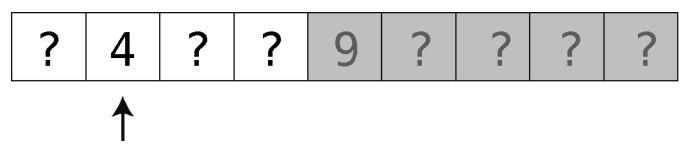
它的值为4,那么7就在它的右边了。由此4左边的格子也就排除了。

第3步:还剩两个格子里可能有7。我们随便挑个左边的。
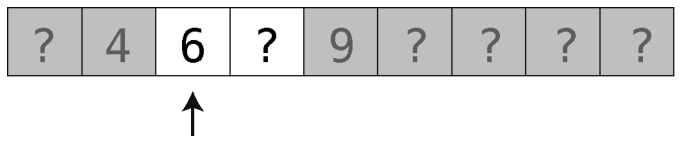
第4步:就剩一个了。(如果还没有,那就说明这个有序数组里真的没有7。)
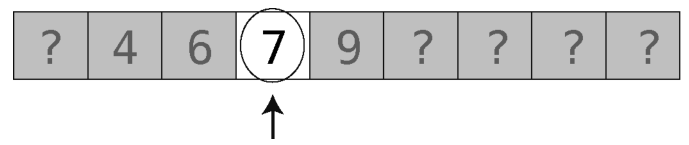
终于找到7了,总共4步。是的,这个有序数组要是用线性查找也会是4步,但稍后你就会见识到二分查找的强大。
以下是二分查找的Ruby实现。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29def binary_search(array, value)
# 首先,设定下界和上界,以限定所查之值可能出现的区域。
# 在开始时,以数组的第一个元素为下界,以最后一个元素为上界
lower_bound = 0
upper_bound = array.length - 1
# 循环检查上界和下界之间的最中间的元素
while lower_bound <= upper_bound do
# 如此找出最中间的格子之索引
#(无须担心商是不是整数,因为 Ruby 总是把两个整数相除所得的小数部分去掉)
midpoint = (upper_bound + lower_bound) / 2
# 获取该中间格子的值
value_at_midpoint = array[midpoint]
# 如果该值正是我们想查的,那就完事了。
# 否则,看你是要往上找还是往下找,来调整下界或上界
if value < value_at_midpoint
upper_bound = midpoint - 1
elsif value > value_at_midpoint
lower_bound = midpoint + 1
elsif value == value_at_midpoint
return midpoint
end
end
# 当下界超越上界,便知数组里并没有我们所要找的值
return nil
end
二分查找与线性查找
对于长度太小的有序数组,二分查找并不比线性查找好多少。但我们来看看更大的数组。
对于拥有100个值的数组来说,两种查找需要的最多步数如下所示。
- 线性查找:100步
- 二分查找:7步
用线性查找的话,如果要找的值在最后一个格子,或者比最后一格的值还大,那么就得查遍每个格子。有100个格子,就是100步。
二分查找则会在每次猜测后排除掉一半的元素。100个格子,在第一次猜测后,便排除了50个。
再换个角度来看,你就会发现一个规律。
长度为3的有序数组,二分查找所需的最多步数是2。
若长度翻倍,变成7(以奇数为例会方便选择正中间的格子,于是我们把长度翻倍后又增加了一个数),则最多步数会是3。
若再翻倍(并加1),变成15个元素,那么最多步数会是4。
规律就是,每次有序数组长度乘以2,二分查找所需的最多步数只会加1。
这真是出奇地高效。
相反,在3个元素的数组上线性查找,最多要3步,7个元素就最多要7步,100个元素就最多要100步,即元素有多少,最多步数就是多少。数组长度翻倍,线性查找的最多步数就会翻倍,而二分查找则只是增加1步。
这种规律可以用下图来展示。
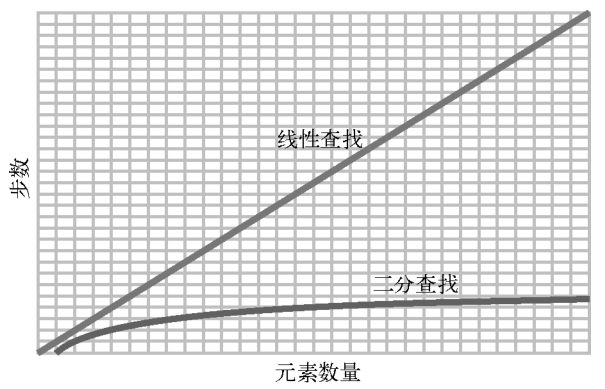
如果数组变得更大,比如说10000个元素,那么线性查找最多会有10000步,而二分查找最多只有14步。再增大到1000000个元素,则线性查找最多有1000000步,二分查找最多只有20步。
不过还要记住,有序数组并不是所有操作都比常规数组要快。如你所见,它的插入就相对要慢。衡量起来,虽然插入是慢了一些,但查找却快了许多。还是那句话,你得根据应用场景来判断哪种更合适。
总结
关于算法的内容就是这些。很多时候,计算一样东西并不只有一种方法,换种算法可能会极大地影响程序的性能。
同时你还应意识到,世界上并没有哪种适用于所有场景的数据结构或者算法。你不能因为有序数组能使用二分查找就永远只用有序数组。在经常插入而很少查找的情况下,显然插入迅速的常规数组会是更好的选择。
如之前所述,比较算法的方式就是比较各自的步数。
下一章,我们将会学习如何规范地描述数据结构和算法的时间复杂度。有了这种通用的表达方式,就能更容易地观察出哪种算法符合我们的实际需求。