思考并回答以下问题:
本章内容
- 学习动态规划,这是一种解决棘手问题的方法,它将问题分成小问题,并先着手解决这些小问题。
- 学习如何设计问题的动态规划解决方案。
背包问题
我们再来看看第8章的背包问题。假设你是个小偷,背着一个可装4磅东西的背包。
你可盗窃的商品有如下3件。
| 音响 | 3000美元 | 4磅 |
| 笔记本电脑 | 2000美元 | 3磅 |
| 吉他 | 1500美元 | 1磅 |
为了让盗窃的商品价值最高,你该选择哪些商品?
简单算法
最简单的算法如下:尝试各种可能的商品组合,并找出价值最高的组合。
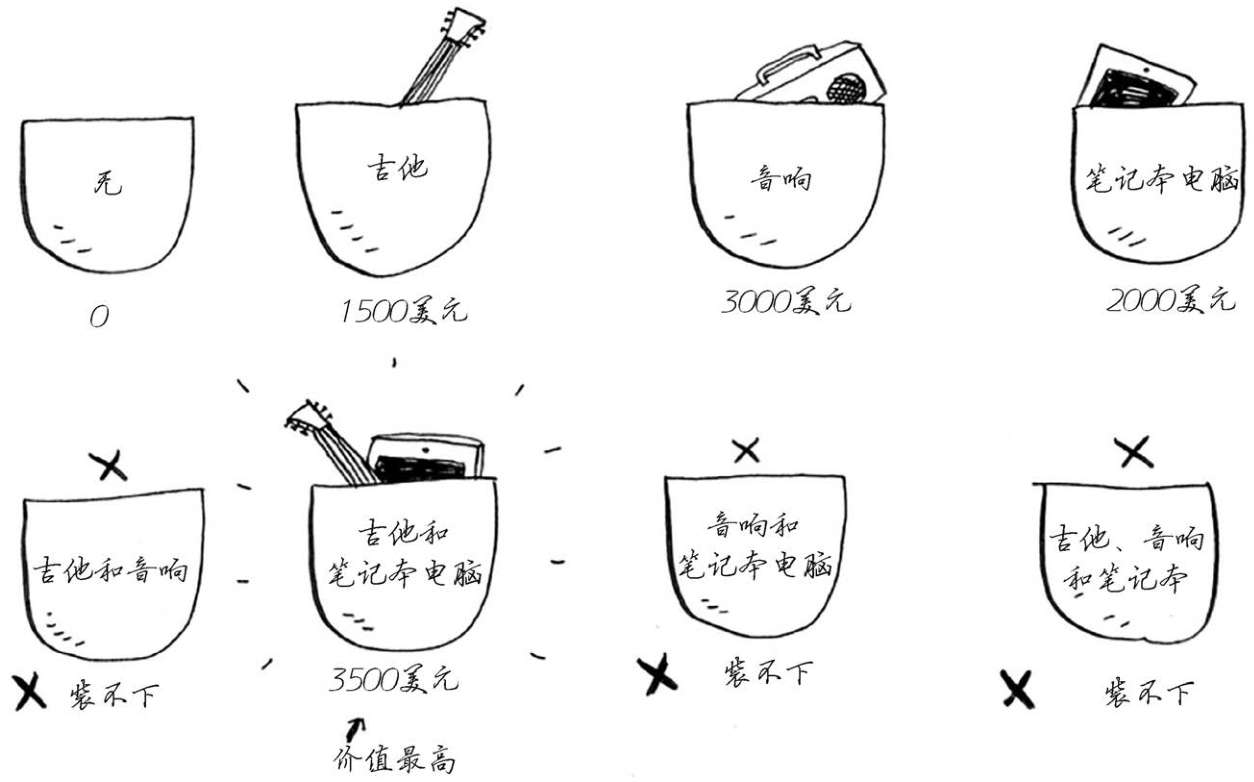
这样可行,但速度非常慢。在有3件商品的情况下,你需要计算8个不同的集合;有4件商品时,你需要计算16个集合。每增加一件商品,需要计算的集合数都将翻倍!这种算法的运行时间为O(2n),真的是慢如蜗牛。
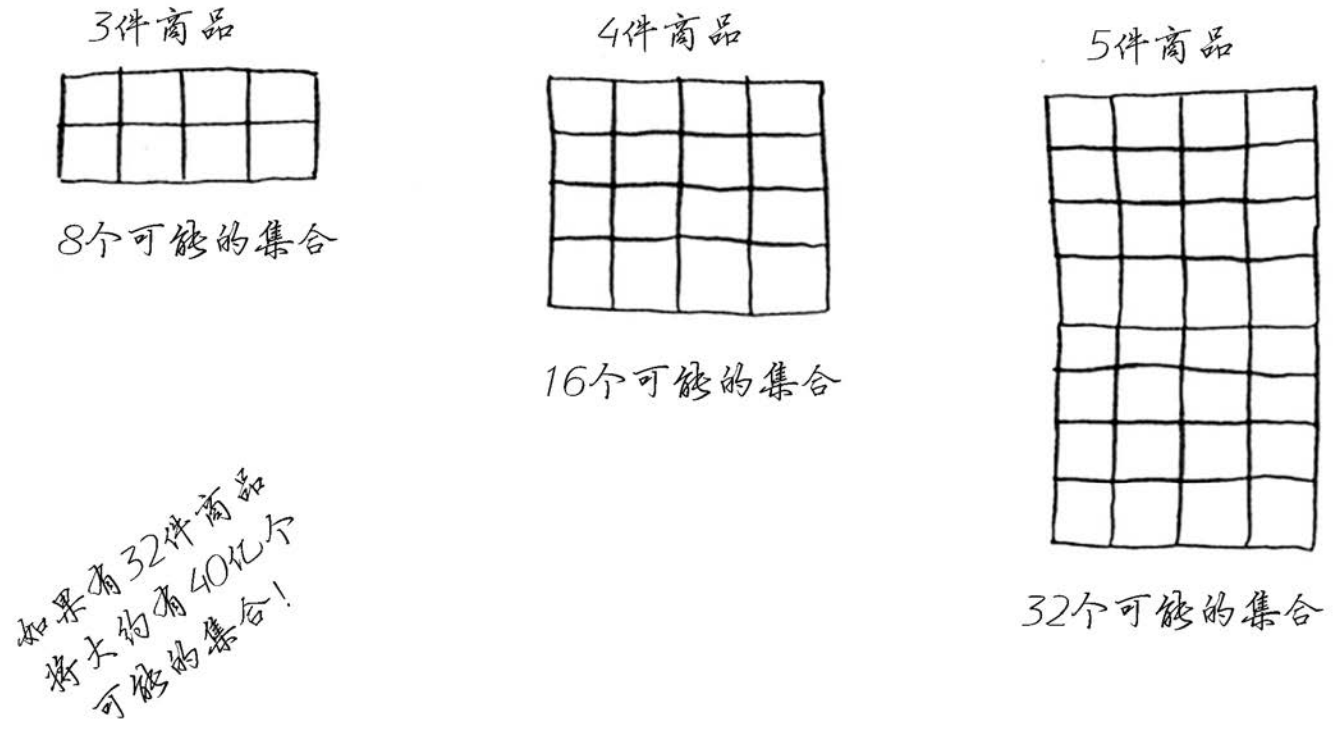
只要商品数量多到一定程度,这种算法就行不通。在第8章,你学习了如何找到近似解,这接近最优解,但可能不是最优解。
那么如何找到最优解呢?
动态规划
答案是使用动态规划!下面来看看动态规划算法的工作原理。动态规划先解决子问题,再逐步解决大问题。
对于背包问题,你先解决小背包(子背包)问题,再逐步解决原来的问题。
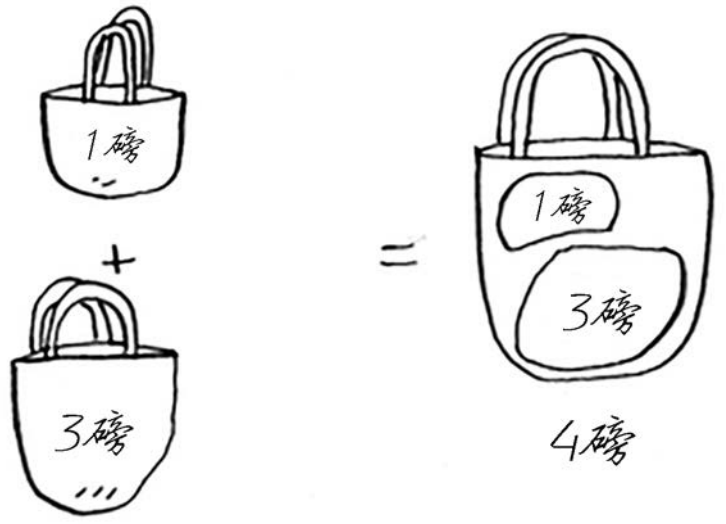
动态规划是一个难以理解的概念,如果你没有立即搞懂,也不用担心,我们将研究很多示例。
先来演示这种算法的执行过程。看过执行过程后,你心里将有一大堆问题!我将竭尽所能解答这些问题。
每个动态规划算法都从一个网格开始,背包问题的网格如下。
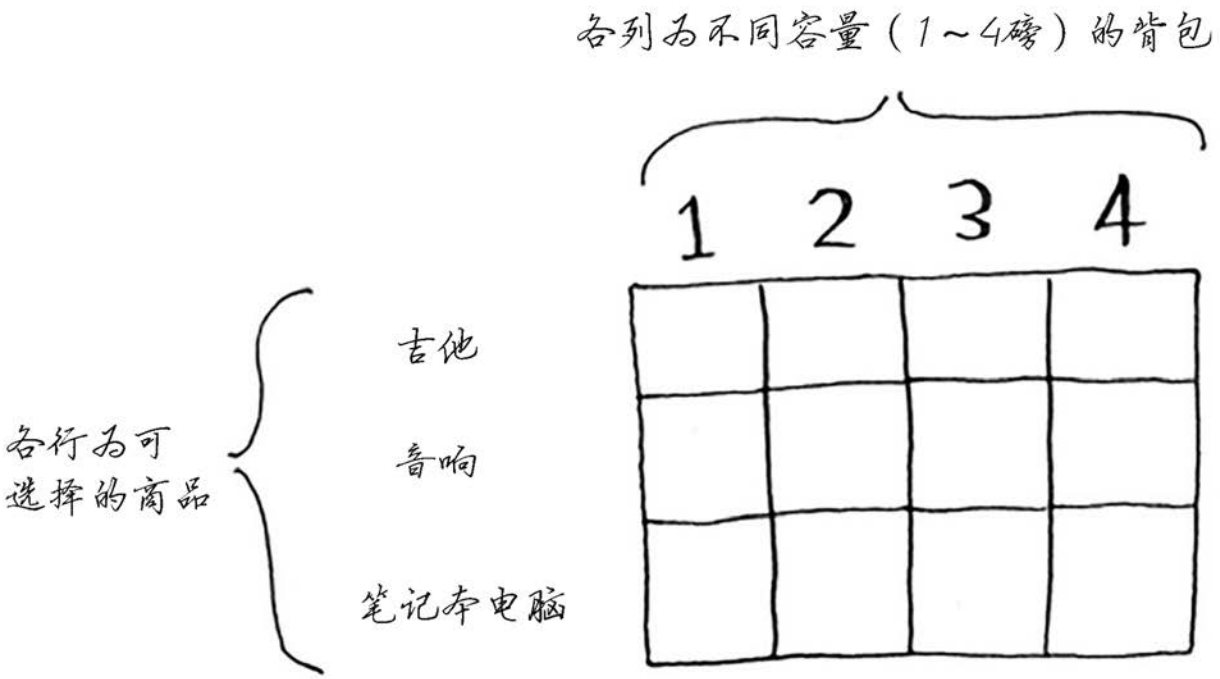
网格的各行为商品,各列为不同容量(1~4磅)的背包。所有这些列你都需要,因为它们将帮助你计算子背包的价值。
网格最初是空的。你将填充其中的每个单元格,网格填满后,就找到了问题的答案!你一定要跟着做。请你创建网格,我们一起来填满它。
1.吉他行
后面将列出计算这个网格中单元格值的公式。我们先来一步一步做。首先来看第一行。
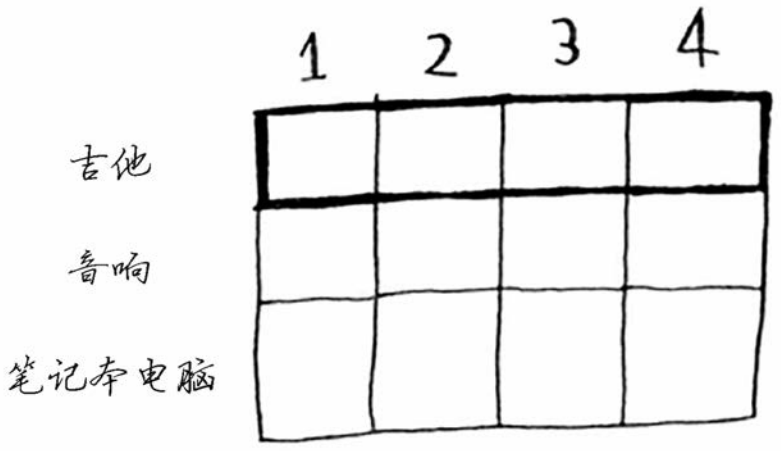
这是吉他行,意味着你将尝试将吉他装入背包。在每个单元格,都需要做一个简单的决定:偷不偷吉他?别忘了,你要找出一个价值最高的商品集合。
第一个单元格表示背包的容量为1磅。吉他的重量也是1磅,这意味着它能装入背包!因此这个单元格包含吉他,价值为1500美元。
下面来开始填充网格。
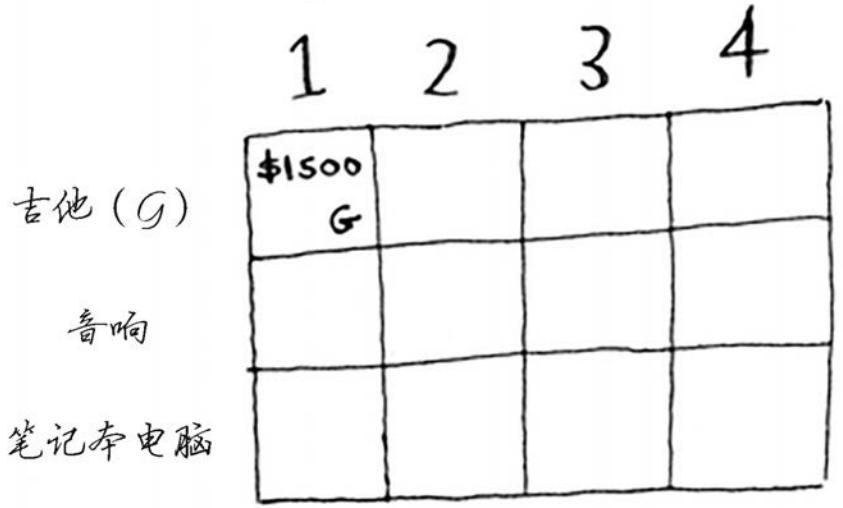
与这个单元格一样,每个单元格都将包含当前可装入背包的所有商品。
来看下一个单元格。这个单元格表示背包的容量为2磅,完全能够装下吉他!
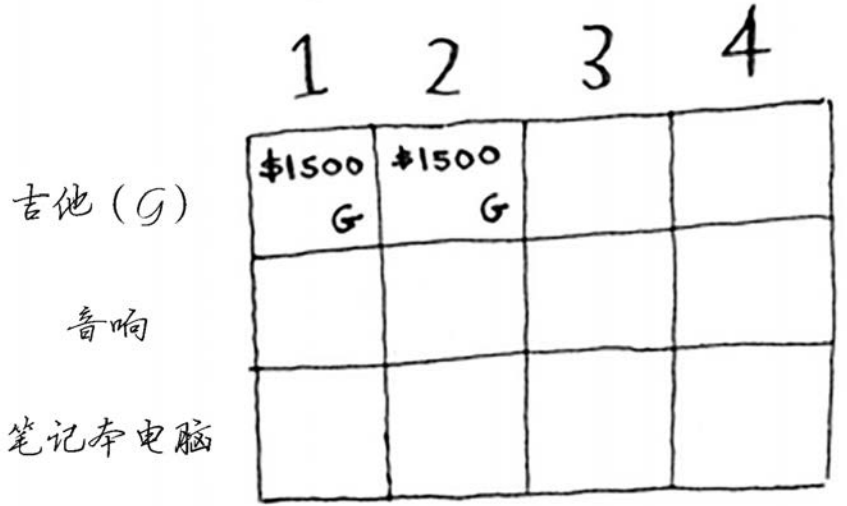
这行的其他单元格也一样。别忘了,这是第一行,只有吉他可供你选择。换言之,你假装现在还没法盗窃其他两件商品。
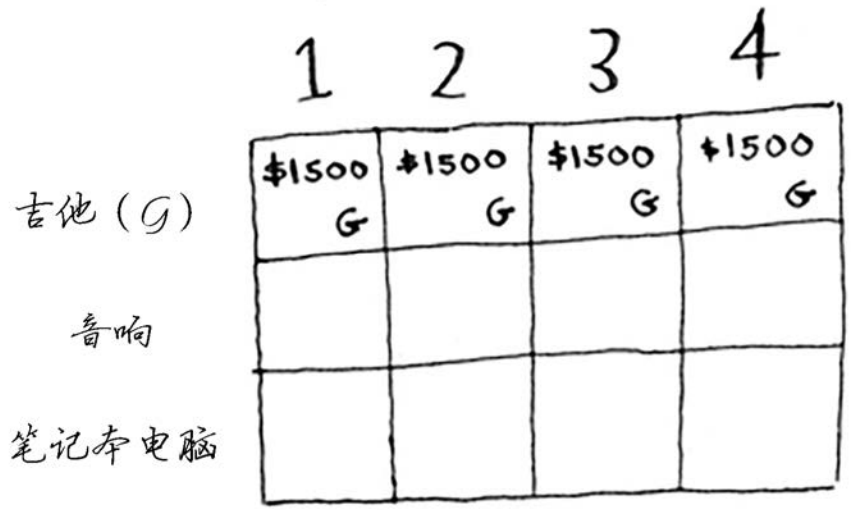
此时你很可能心存疑惑:原来的问题说的是4磅的背包,我们为何要考虑容量为1磅、2磅等的背包呢?前面说过,动态规划从小问题着手,逐步解决大问题。这里解决的子问题将帮助你解决大问题。请接着往下读,稍后你就会明白的。
此时网格应类似于下面这样。
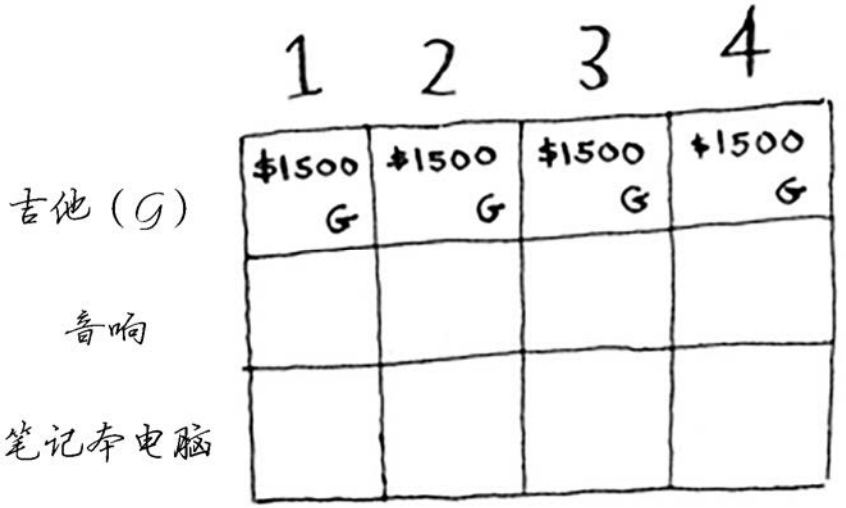
别忘了,你要做的是让背包中商品的价值最大。这行表示的是当前的最大价值。它指出,如果你有一个容量4磅的背包,可在其中装入的商品的最大价值为1500美元。
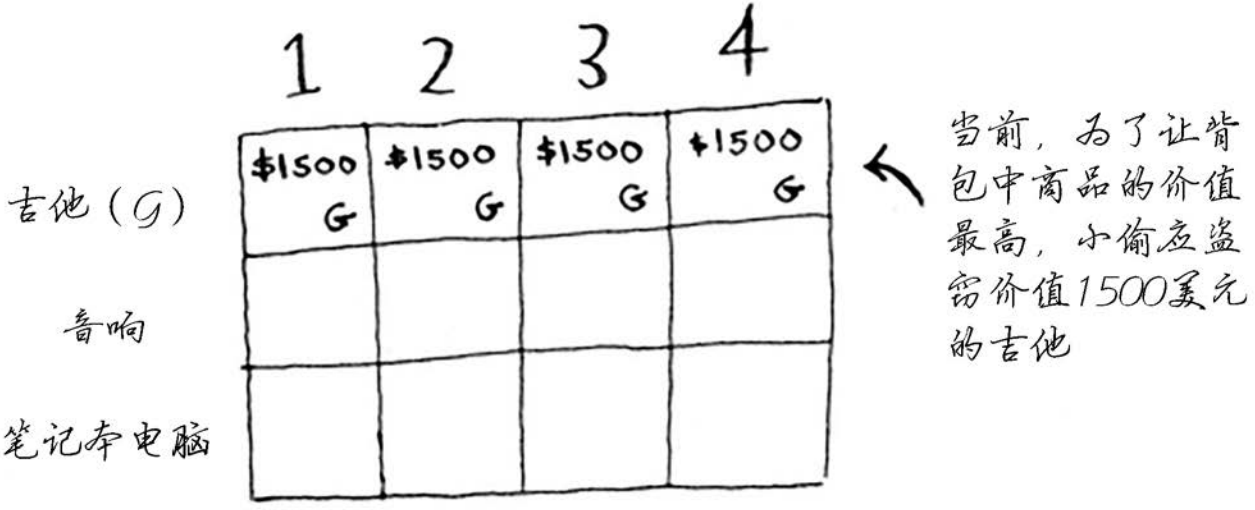
你知道这不是最终的解。随着算法往下执行,你将逐步修改最大价值。
2.音响行
我们来填充下一行——音响行。你现在处于第二行,可偷的商品有吉他和音响。在每一行,可偷的商品都为当前行的商品以及之前各行的商品。因此,当前你还不能偷笔记本电脑,而只能偷音响和吉他。我们先来看第一个单元格,它表示容量为1磅的背包。在此之前,可装入1磅背包的商品的最大价值为1500美元。
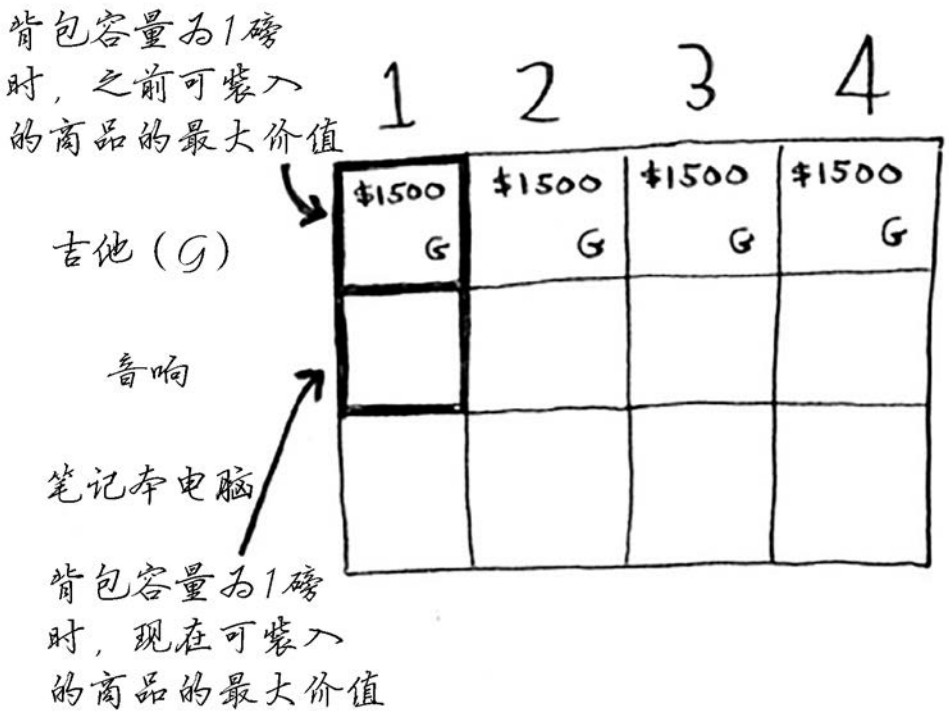
该不该偷音响呢?
背包的容量为1磅,能装下音响吗?音响太重了,装不下!由于容量1磅的背包装不下音响,因此最大价值依然是1500美元。
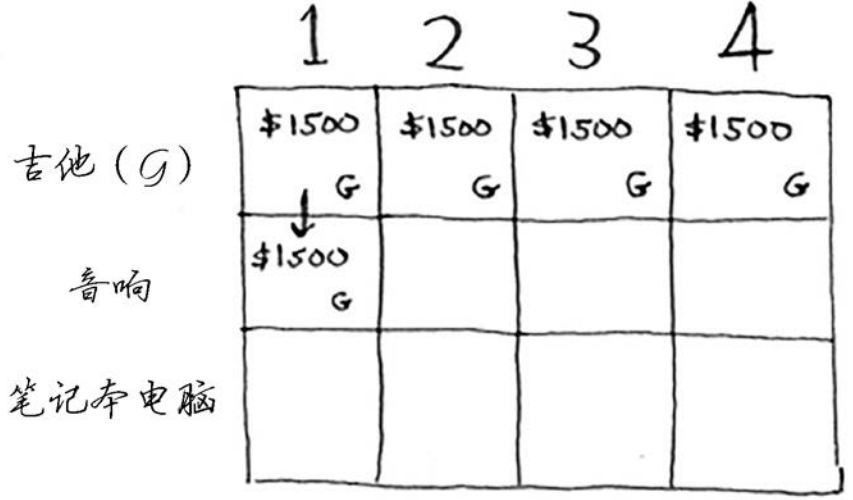
接下来的两个单元格的情况与此相同。在这些单元格中,背包的容量分别为2磅和3磅,而以前的最大价值为1500美元。
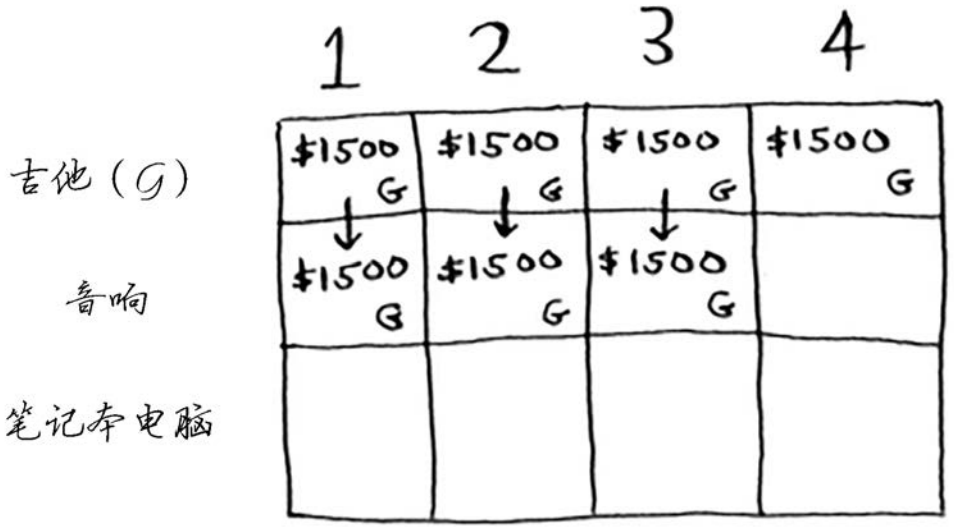
由于这些背包装不下音响,因此最大价值保持不变。
背包容量为4磅呢?终于能够装下音响了!原来的最大价值为1500美元,但如果在背包中装入音响而不是吉他,价值将为3000美元!因此还是偷音响吧。
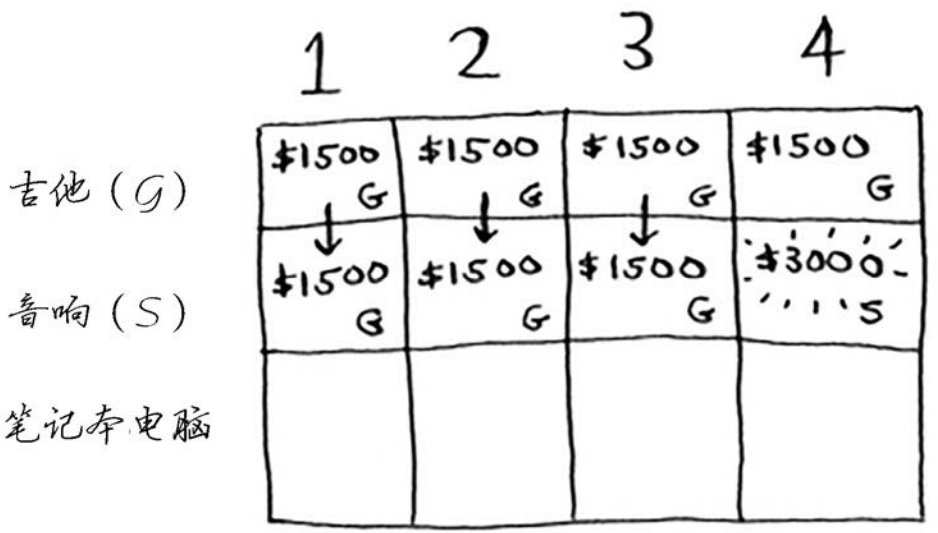
你更新了最大价值!如果背包的容量为4磅,就能装入价值至少3000美元的商品。在这个网格中,你逐步地更新最大价值。
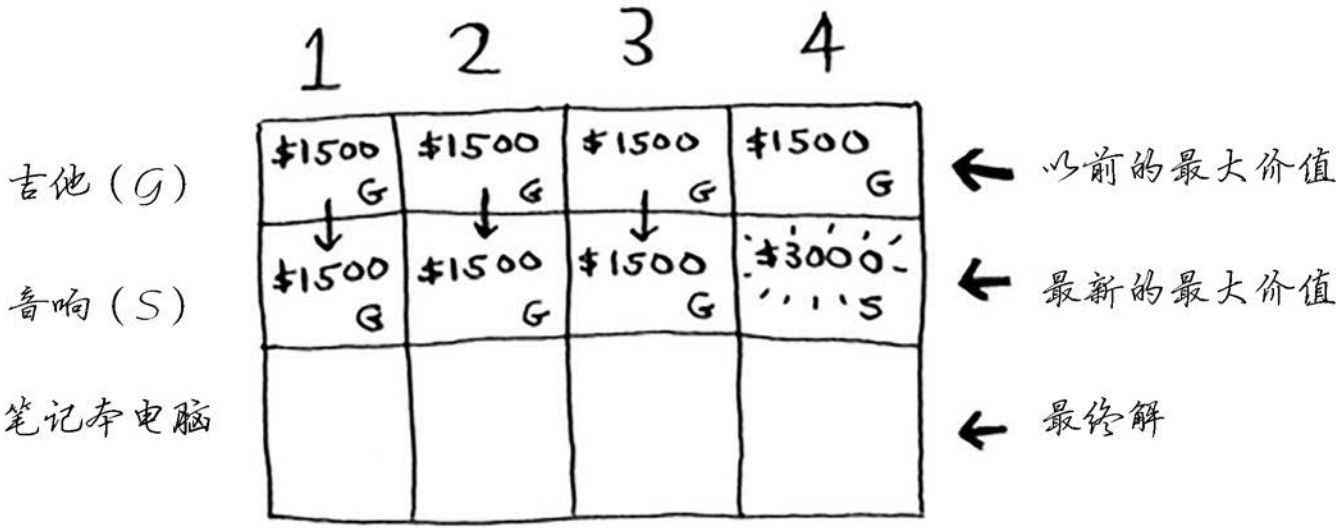
3.笔记本电脑行
下面以同样的方式处理笔记本电脑。笔记本电脑重3磅,没法将其装入容量为1磅或2磅的背包,因此前两个单元格的最大价值还是1500美元。
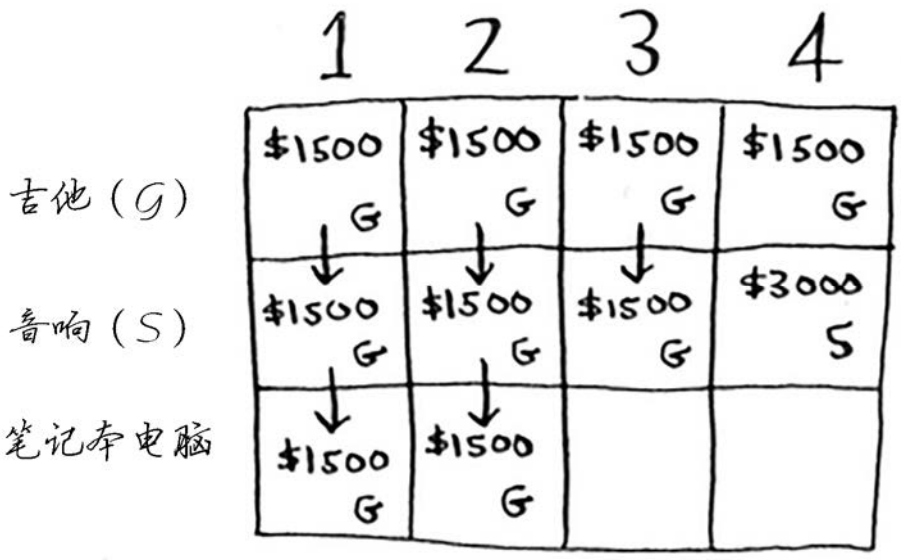
对于容量为3磅的背包,原来的最大价值为1500美元,但现在你可选择盗窃价值2000美元的笔记本电脑而不是吉他,这样新的最大价值将为2000美元!
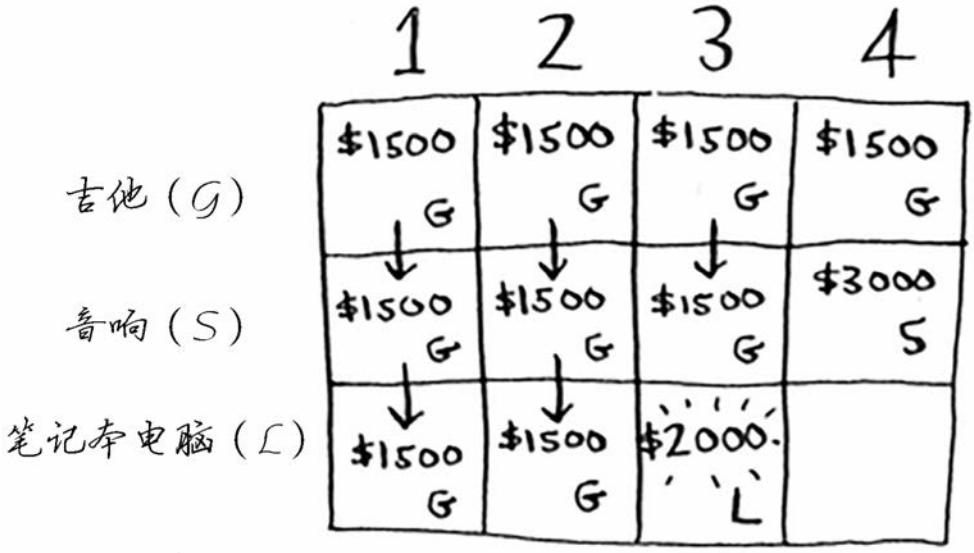
对于容量为4磅的背包,情况很有趣。这是非常重要的部分。当前的最大价值为3000美元,你可不偷音响,而偷笔记本电脑,但它只值2000美元。

价值没有原来高。但等一等,笔记本电脑的重量只有3磅,背包还有1磅的容量没用!

在1磅的容量中,可装入的商品的最大价值是多少呢?你之前计算过。
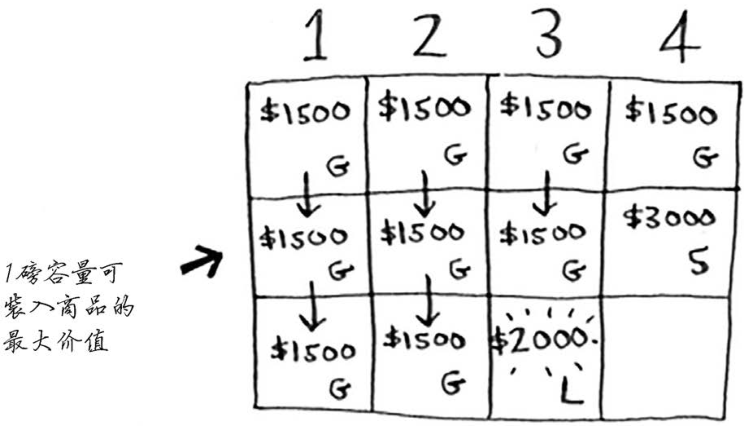
根据之前计算的最大价值可知,在1磅的容量中可装入吉他,价值1500美元。因此,你需要做如下比较。

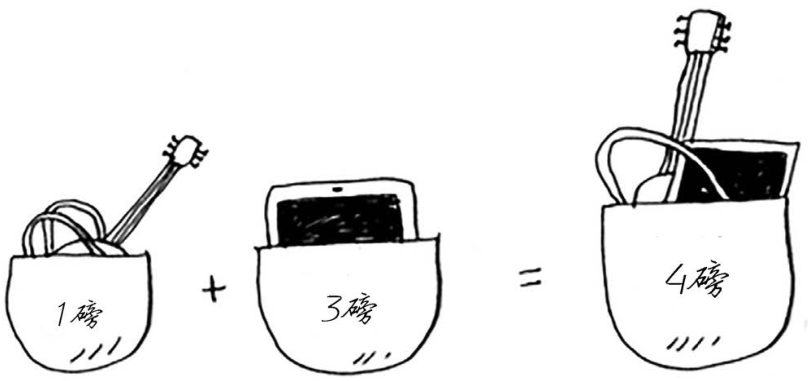
你可能始终心存疑惑:为何计算小背包可装入的商品的最大价值呢?但愿你现在明白了其中的原因!余下了空间时,你可根据这些子问题的答案来确定余下的空间可装入哪些商品。笔记本电脑和吉他的总价值为3500美元,因此偷它们是更好的选择。
最终的网格类似于下面这样。
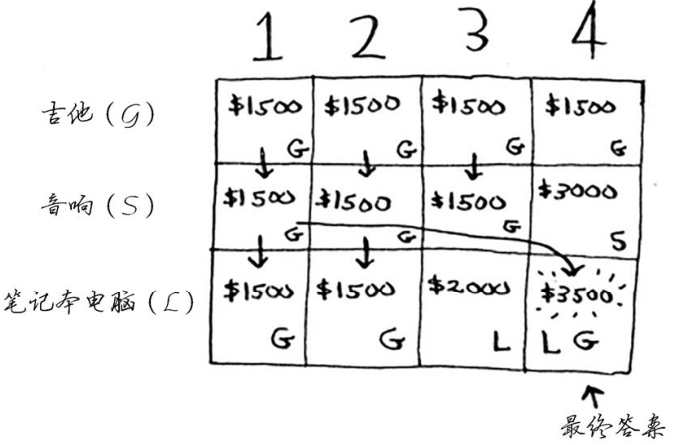
答案如下:将吉他和笔记本电脑装入背包时价值最高,为3500美元。
你可能认为,计算最后一个单元格的价值时,我使用了不同的公式。那是因为填充之前的单元格时,我故意避开了一些复杂的因素。其实,计算每个单元格的价值时,使用的公式都相同。这个公式如下。

你可以使用这个公式来计算每个单元格的价值,最终的网格将与前一个网格相同。现在你明白了为何要求解子问题吧?你可以合并两个子问题的解来得到更大问题的解。
背包问题FAQ
你可能还是觉得这像是变魔术。本节将回答一些常见的问题。
再增加一件商品将如何呢
假设你发现还有第四件商品可偷——一个价值2000美元重量为1磅的iPhone!
此时需要重新执行前面所做的计算吗?不需要。别忘了,动态规划逐步计算最大价值。到目前为止,计算出的最大价值如下。
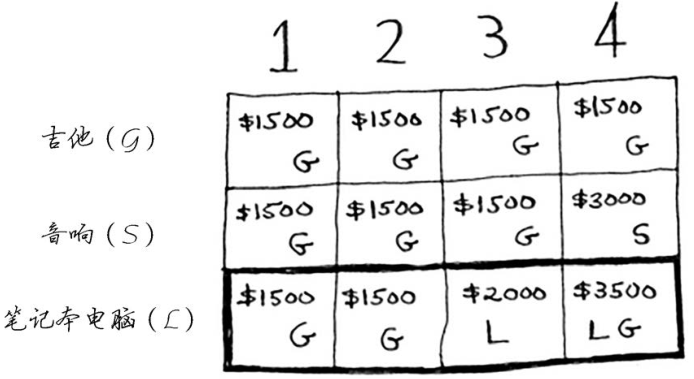
这意味着背包容量为4磅时,你最多可偷价值3500美元的商品。但这是以前的情况,下面再添加表示iPhone的行。
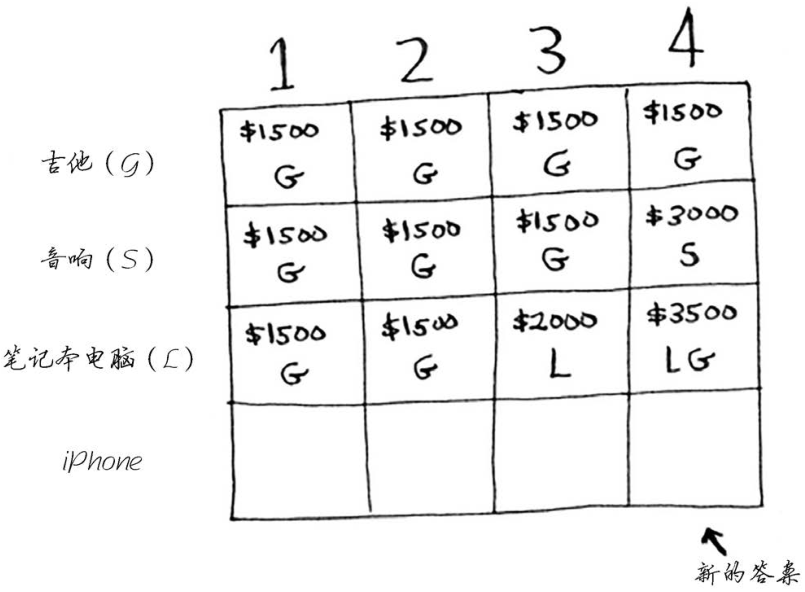
最大价值可能发生变化!请尝试填充这个新增的行,再接着往下读。
我们从第一个单元格开始。iPhone可装入容量为1磅的背包。之前的最大价值为1500美元,但iPhone价值2000美元,因此该偷iPhone而不是吉他。
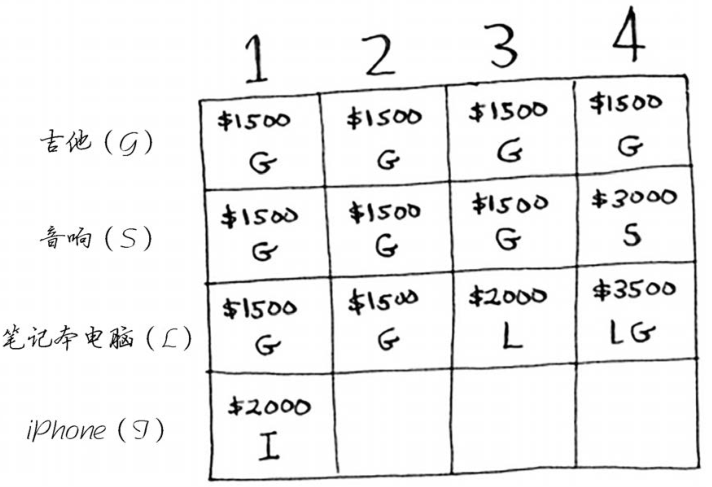
在下一个单元格中,你可装入iPhone和吉他。
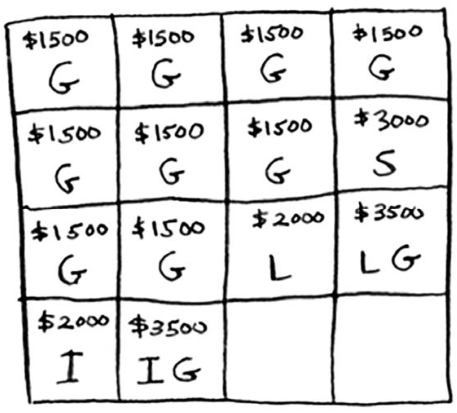
对于第三个单元格,也没有比装入iPhone和吉他更好的选择了。
对于最后一个单元格,情况比较有趣。当前的最大价值为3500美元,但你可偷iPhone,这将余下3磅的容量。

3磅容量的最大价值为2000美元!再加上iPhone价值2000美元,总价值为4000美元。新的最大价值诞生了!
最终的网格如下。
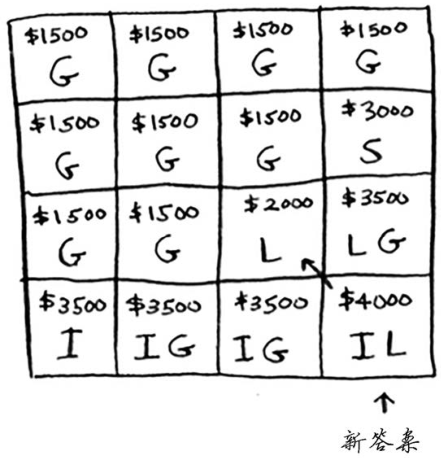
问题:沿着一列往下走时,最大价值有可能降低吗?
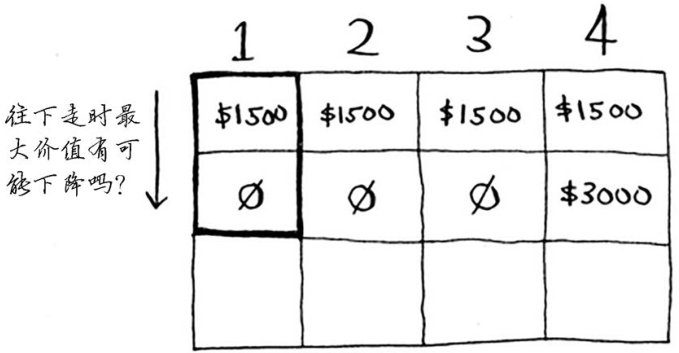
请找出这个问题的答案,再接着往下读。
答案:不可能。每次迭代时,你都存储当前的最大价值。最大价值不可能比以前低!
练习
1.假设你还可偷另外一件商品——MP3播放器,它重1磅,价值1000美元。你要偷吗?
行的排列顺序发生变化时结果将如何
答案会随之变化吗?假设你按如下顺序填充各行:音响、笔记本电脑、吉他。网格将会是什么样的?请自己动手填充这个网格,再接着往下读。
网格将类似于下面这样。
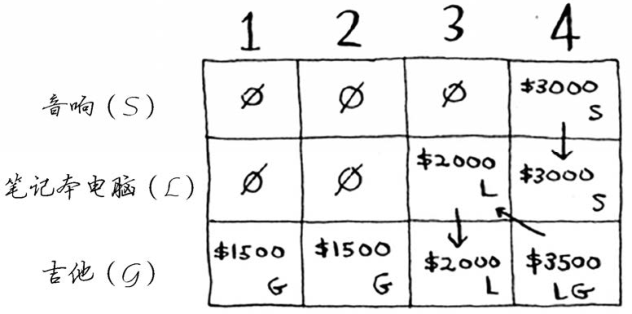
答案没有变化。也就是说,各行的排列顺序无关紧要。
可以逐列而不是逐行填充网格吗
自己动手试试吧!就这个问题而言,这没有任何影响,但对于其他问题,可能有影响。
增加一件更小的商品将如何呢
假设你还可以偷一条项链,它重0.5磅,价值1000美元。前面的网格都假设所有商品的重量为整数,但现在你决定把项链给偷了,因此余下的容量为3.5磅。在3.5磅的容量中,可装入的商品的最大价值是多少呢?不知道!因为你只计算了容量为1磅、2磅、3磅和4磅的背包可装下的商品的最大价值。现在,你需要知道容量为3.5磅的背包可装下的商品的最大价值。
由于项链的加入,你需要考虑的粒度更细,因此必须调整网格。
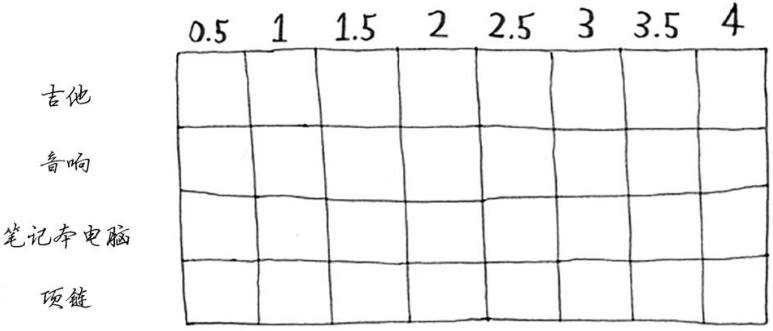
可以偷商品的一部分吗
假设你在杂货店行窃,可偷成袋的扁豆和大米,但如果整袋装不下,可打开包装,再将背包倒满。在这种情况下,不再是要么偷要么不偷,而是可偷商品的一部分。如何使用动态规划来处理这种情形呢?
答案是没法处理。使用动态规划时,要么考虑拿走整件商品,要么考虑不拿,而没法判断该不该拿走商品的一部分。
但使用贪婪算法可轻松地处理这种情况!首先,尽可能多地拿价值最高的商品;如果拿光了,再尽可能多地拿价值次高的商品,以此类推。
例如,假设有如下商品可供选择。

藜麦比其他商品都值钱,因此要尽量往背包中装藜麦!如果能够在背包中装满藜麦,结果就是最佳的。
如果藜麦装完后背包还没满,就接着装入下一种最值钱的商品,以此类推。
旅游行程最优化
假设你要去伦敦度假,假期两天,但你想去游览的地方很多。你没法前往每个地方游览,因此你列个单子。
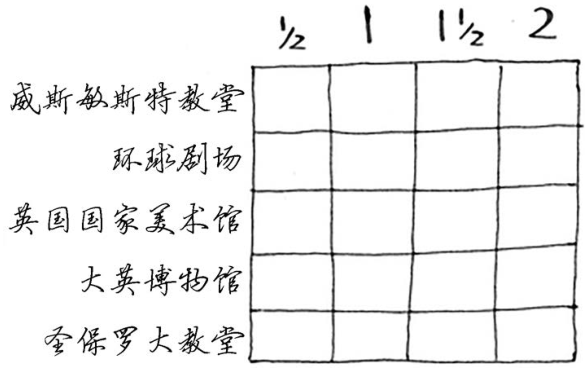
对于想去游览的每个名胜,都列出所需的时间以及你有多想去看看。根据这个清单,你能确定该去游览哪些名胜吗?
这也是一个背包问题!但约束条件不是背包的容量,而是有限的时间;不是决定该装入哪些商品,而是决定该去游览哪些名胜。请根据这个清单绘制动态规划网格,再接着往下读。
网格类似于下面这样。
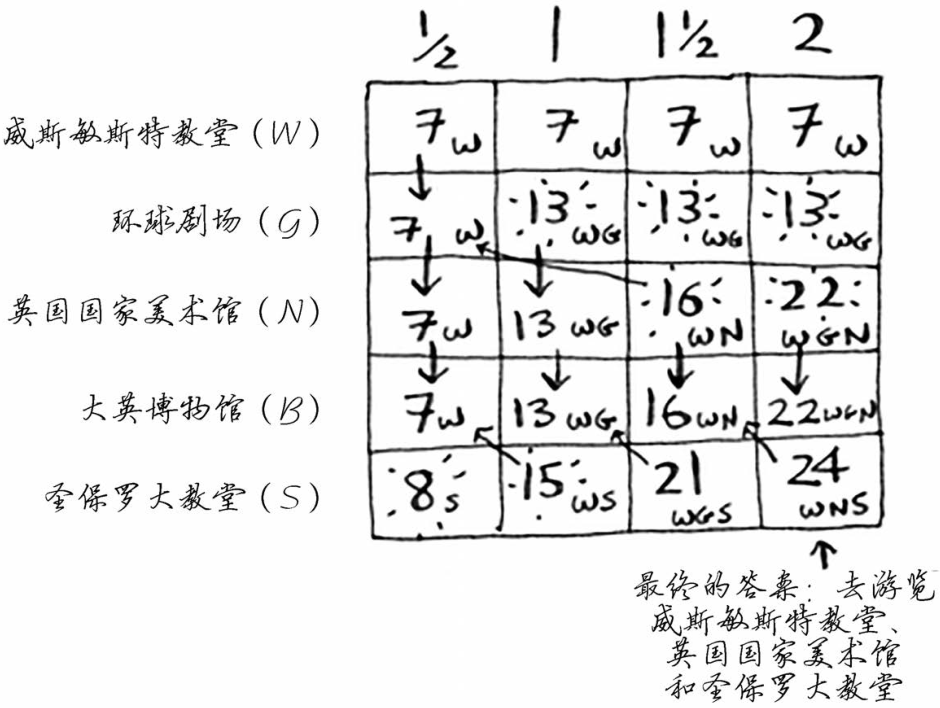
你画对了吗?请填充这个网格,决定该游览哪些名胜。答案如下。

处理相互依赖的情况
假设你还想去巴黎,因此在前述清单中又添加了几项。
去这些地方游览需要很长时间,因为你先得从伦敦前往巴黎,这需要半天时间。如果这3个地方都去玩,是不是要4.5天呢?
不是的,因为不是去每个地方都得先从伦敦到巴黎。到达巴黎后,每个地方都只需1天时间。因此玩这3个地方需要的总时间为3.5天(半天从伦敦到巴黎,每个地方1天),而不是4.5天。
将埃菲尔铁塔加入“背包”后,卢浮宫将更“便宜”:只要1天时间,而不是1.5天。如何使用动态规划对这种情况建模呢?
没办法建模。动态规划功能强大,它能够解决子问题并使用这些答案来解决大问题。但仅当每个子问题都是离散的,即不依赖于其他子问题时,动态规划才管用。这意味着使用动态规划算法解决不了去巴黎玩的问题。
计算最终的解时会涉及两个以上的子背包吗
为获得前述背包问题的最优解,可能需要偷两件以上的商品。但根据动态规划算法的设计,最多只需合并两个子背包,即根本不会涉及两个以上的子背包。不过这些子背包可能又包含子背包。
最优解可能导致背包没装满吗
完全可能。假设你还可以偷一颗钻石。
这颗钻石非常大,重达3.5磅,价值100万美元,比其他商品都值钱得多。
你绝对应该把它给偷了!但当你这样做时,余下的容量只有0.5磅,别的什么都装不下。
练习
2.假设你要去野营。你有一个容量为6磅的背包,需要决定该携带下面的哪些东西。其中每样东西都有相应的价值,价值越大意味着越重要:
- 水(重3磅,价值10);
- 书(重1磅,价值3)
- 食物(重2磅,价值9);
- 夹克(重2磅,价值5);
- 相机(重1磅,价值6)。
请问携带哪些东西时价值最高?
最长公共子串
通过前面的动态规划问题,你得到了哪些启示呢?
- 动态规划可帮助你在给定约束条件下找到最优解。在背包问题中,你必须在背包容量给定的情况下,偷到价值最高的商品。
- 在问题可分解为彼此独立且离散的子问题时,就可使用动态规划来解决。
要设计出动态规划解决方案可能很难,这正是本节要介绍的。下面是一些通用的小贴士。
- 每种动态规划解决方案都涉及网格。
- 单元格中的值通常就是你要优化的值。在前面的背包问题中,单元格的值为商品的价值。
- 每个单元格都是一个子问题,因此你应考虑如何将问题分成子问题,这有助于你找出网格的坐标轴。
下面再来看一个例子。假设你管理着网站dictionary.com。用户在该网站输入单词时,你需要给出其定义。
但如果用户拼错了,你必须猜测他原本要输入的是什么单词。例如,Alex想查单词fish,但不小心输入了hish。在你的字典中,根本就没有这样的单词,但有几个类似的单词。
在这个例子中,只有两个类似的单词,真是太小儿科了。实际上,类似的单词很可能有数千个。
Alex输入了hish,那他原本要输入的是fish还是vista呢?
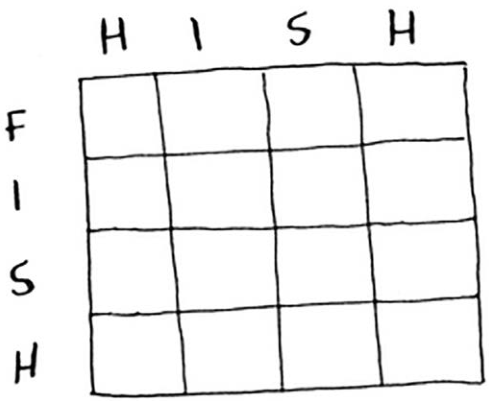
绘制网格
用于解决这个问题的网格是什么样的呢?要确定这一点,你得回答如下问题。
- 单元格中的值是什么?
- 如何将这个问题划分为子问题?
- 网格的坐标轴是什么?
在动态规划中,你要将某个指标最大化。在这个例子中,你要找出两个单词的最长公共子串。hish和fish都包含的最长子串是什么呢?hish和vista呢?这就是你要计算的值。
别忘了,单元格中的值通常就是你要优化的值。在这个例子中,这很可能是一个数字:两个字符串都包含的最长子串的长度。
如何将这个问题划分为子问题呢?你可能需要比较子串:不是比较hish和fish,而是先比较his和fis。每个单元格都将包含这两个子串的最长公共子串的长度。这也给你提供了线索,让你觉得坐标轴很可能是这两个单词。因此,网格可能类似于下面这样。

如果这在你看来犹如巫术,也不用担心。这些内容很难懂,但这也正是我到现在才介绍它们的原因!本章后面有一个练习,到时你可以自己动手来进行动态规划。
填充网格
现在,你很清楚网格应是什么样的。填充该网格的每个单元格时,该使用什么样的公式呢?由于你已经知道答案——hish和fish的最长公共子串为ish,因此可以作点弊。
即便如此,你还是不能确定该使用什么样的公式。计算机科学家有时会开玩笑说,那就使用费曼算法(Feynman algorithm)。这个算法是以著名物理学家理查德·费曼命名的,其步骤如下。
(1) 将问题写下来。
(2) 好好思考。
(3) 将答案写下来。
计算机科学家真是一群不按常理出牌的人啊!
实际上,根本没有找出计算公式的简单办法,你必须通过尝试才能找出管用的公式。有些算法并非精确的解决步骤,而只是帮助你理清思路的框架。
请尝试为这个问题找到计算单元格值的公式。给你一点提示吧:下面是这个单元格的一部分。
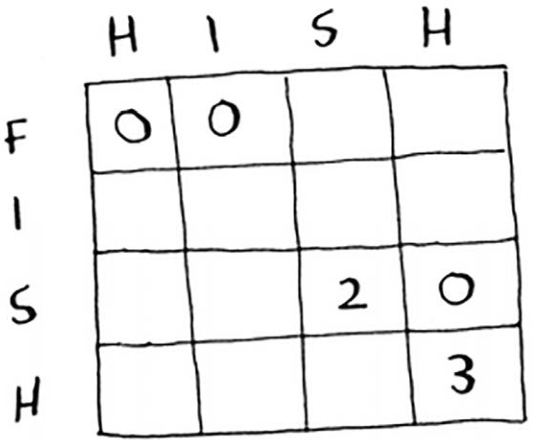
其他单元格的值呢?别忘了,每个单元格都是一个子问题的值。为何单元格(3,3)的值为2呢?
又为何单元格(3, 4)的值为0呢?
请找出计算公式,再接着往下读。这样即便你没能找出正确的公式,后面的解释也将容易理解得多。
揭晓答案
最终的网格如下。
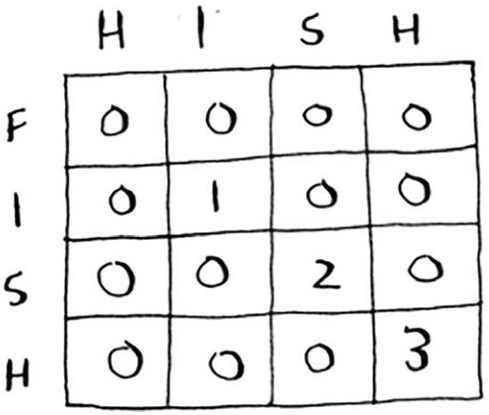
我使用下面的公式来计算每个单元格的值。
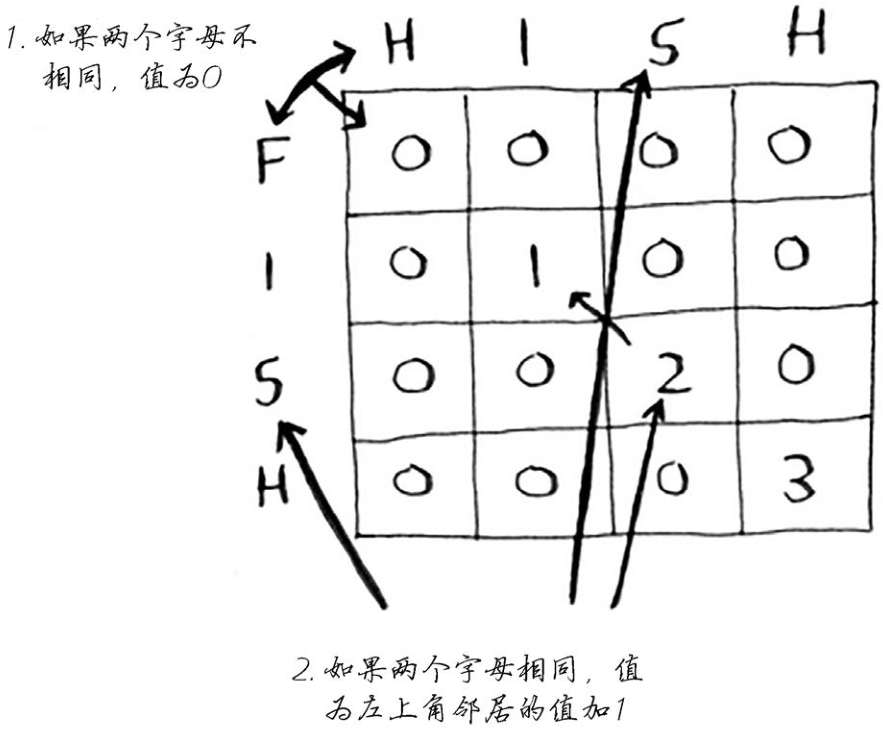
实现这个公式的伪代码类似于下面这样。
1 | if word_a[i] == word_b[j]: # 两个字母相同 |
查找单词hish和vista的最长公共子串时,网格如下。
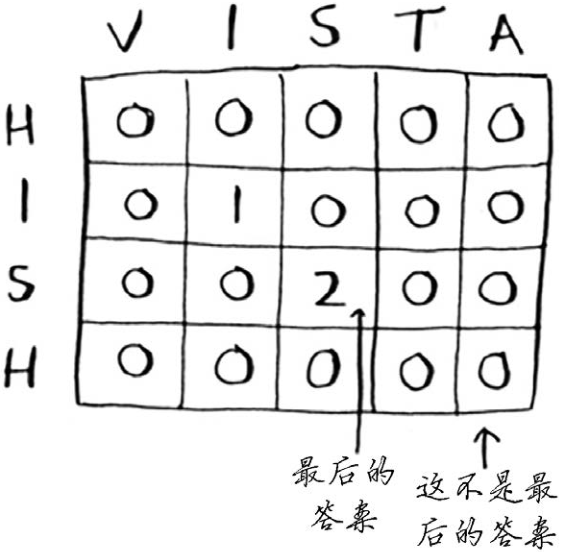
需要注意的一点是,这个问题的最终答案并不在最后一个单元格中!对于前面的背包问题,最终答案总是在最后的单元格中。但对于最长公共子串问题,答案为网格中最大的数字——它可能并不位于最后的单元格中。
我们回到最初的问题:哪个单词与hish更像?hish和fish的最长公共子串包含三个字母,而hish和vista的最长公共子串包含两个字母。
因此Alex很可能原本要输入的是fish。
最长公共子序列
假设Alex不小心输入了fosh,他原本想输入的是fish还是fort呢?
我们使用最长公共子串公式来比较它们。
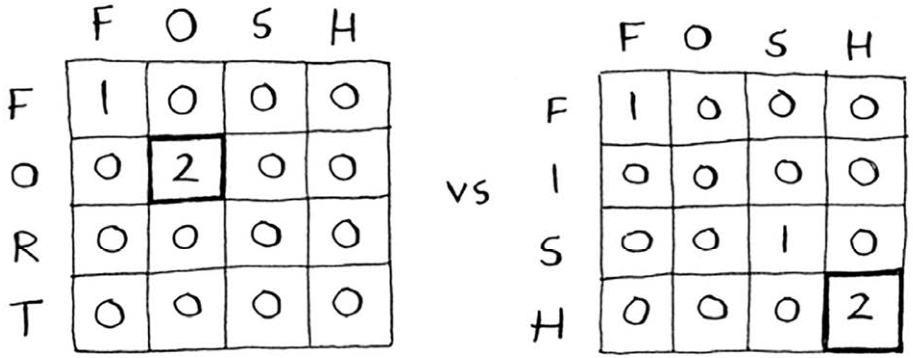
最长公共子串的长度相同,都包含两个字母!但fosh与fish更像。
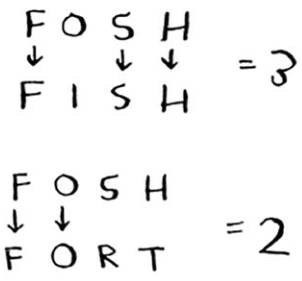
这里比较的是最长公共子串,但其实应比较最长公共子序列:两个单词中都有的序列包含的字母数。如何计算最长公共子序列呢?
下面是用于计算fish和fosh的最长公共子序列的网格的一部分。
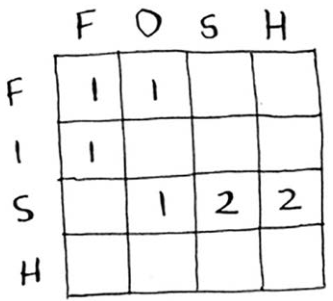
你能找出填充这个网格时使用的公式吗?最长公共子序列与最长公共子串很像,计算公式也很像。请试着找出这个公式——答案稍后揭晓。
最长公共子序列之解决方案
最终的网格如下。
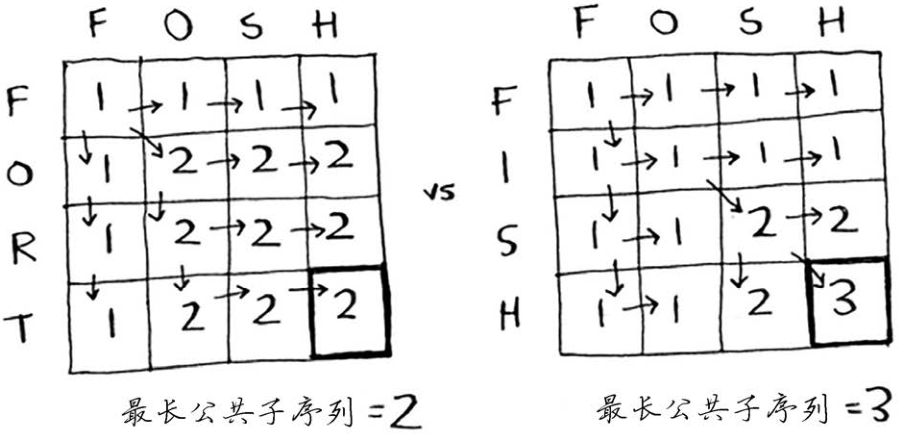
下面是填写各个单元格时使用的公式。
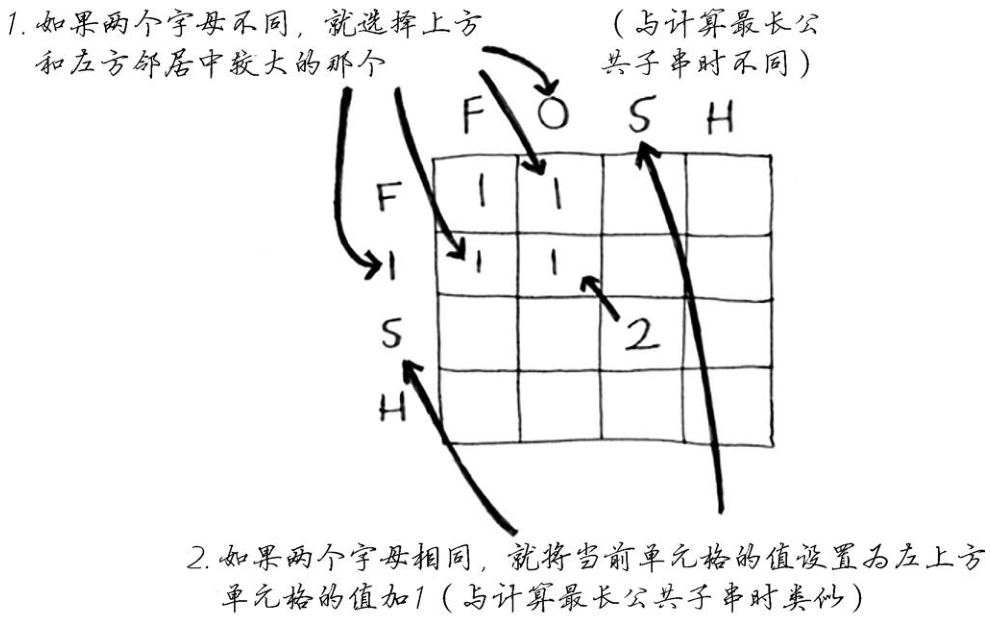
伪代码如下。
1 | if word_a[i] == word_b[j]: # 两个字母相同 |
本章到这里就结束了!它绝对是本书最难理解的一章。动态规划都有哪些实际应用呢?
- 生物学家根据最长公共序列来确定DNA链的相似性,进而判断度两种动物或疾病有多相似。最长公共序列还被用来寻找多发性硬化症治疗方案。
- 你使用过诸如git diff等命令吗?它们指出两个文件的差异,也是使用动态规划实现的。
- 前面讨论了字符串的相似程度。编辑距离(levenshtein distance)指出了两个字符串的相似程度,也是使用动态规划计算得到的。编辑距离算法的用途很多,从拼写检查到判断用户上传的资料是否是盗版,都在其中。
- 你使用过诸如Microsoft Word等具有断字功能的应用程序吗?它们如何确定在什么地方断字以确保行长一致呢?使用动态规划!
练习
3.请绘制并填充用来计算blue和clues最长公共子串的网格。
小结
- 需要在给定约束条件下优化某种指标时,动态规划很有用。
- 问题可分解为离散子问题时,可使用动态规划来解决。
- 每种动态规划解决方案都涉及网格。
- 单元格中的值通常就是你要优化的值。
- 每个单元格都是一个子问题,因此你需要考虑如何将问题分解为子问题。
- 没有放之四海皆准的计算动态规划解决方案的公式。
答案
9.1 要。在这种情况下,你可偷来MP3播放器和iPhone和吉他,总价值为4500美元。
9.2 你应携带水、食物和相机。
9.3
