思考并回答以下问题:
- 什么是大O记法?解答的是什么样的问题?
- O(1)是什么意思?有哪些算法是O(1)?
- O(N)是什么意思?哪些算法是O(N)?
- O(1)和O(N)分别又叫做什么?
- 线性查找的最好情况是O(1),最坏情况是O(N)如何理解?大O记法一般都是指最坏情况如何理解?
- 二分查找的大O记法是什么样的?也叫作什么?
- 什么是对数和指数?
- O(log N)算法是什么意思?
- O(1)、O(log N)、O(N)的效率比较是什么样的?在图中如何表示?
本章涵盖:
- 大O:数步数
- 常数时间与线性时间
- 同一算法,不同场景
- 第三种算法
- 对数
- 解释O(log N)
从之前的章节中我们了解到,影响算法性能的主要因素是其所需的步数。
然而,我们不能简单地把一个算法记为“22步算法”,把另一个算法记为“400步算法”,因为一个算法的步数并不是固定的。以线性查找为例,它的步数等于数组的元素数量。如果数组有22个元素,线性查找就需要22步;如果数组有400个元素,线性查找就需要400步。
量化线性查找效率的更准确的方式应该是:对于具有N个元素的数组,线性查找最多需要N步。当然,这听起来很啰唆。
为了方便表达数据结构和算法的时间复杂度,计算机科学家从数学界借鉴了一种简洁又通用的方式,那就是大O记法。这种规范化语言使得我们可以轻松地指出一个算法的性能级别,也令学术交流变得简单。
掌握了大O记法,就掌握了算法分析的专业工具。
虽说大O记法源于数学领域,但接下来我们不会讲解任何数学术语,只介绍跟计算机科学相关的部分。并且,我们会循序渐进,先用简单的词汇来解释它,然后在接下来的三章中将其构建完善。大O记法不复杂,但我们还是分成了几个章节来细述,使其更容易理解。
大O:数步数
为了统一描述,大O不关注算法所用的时间,只关注其所用的步数。
第1章介绍过,数组不论多大,读取都只需1步。用大O记法来表示,就是:
很多人将其读作“大O1”,也有些人读成“1数量级”。我一般读成“O1”。虽然大O记法有很多种读法,但写法只有一种。
O(1)意味着一种算法无论面对多大的数据量,其步数总是相同的。就像无论数组有多大,读取元素都只要1步。这1步在旧机器上也许要花20分钟,而用现代的硬件却只要1纳秒。但这两种情况下,读取数组都是1步。
其他也属于O(1)的操作还包括数组末尾的插入与删除。之前已证明,无论数组有多大,这两种操作都只需1步,所以它们的效率都是O(1)。
下面研究一下大O记法如何描述线性查找的效率。回想一下,线性查找在数组上要逐个检查每个格子。在最坏情况下,线性查找所需的步数等于格子数。即如前所述:对于N个元素的数组,线性查找需要花N步。
用大O记法来表示,即为:
我将其读作“O N”。
若用大O记法来描述一种处理一个N元素的数组需花N步的算法的效率,很简单,就是O(N)。
数学解释
前面提过,本书要采用一种易于理解的方式来讨论大O。当然这不是唯一的方式,如果你去上传统的大学算法课程,老师很可能从数学角度来介绍大O。因为大O本就是一个数学概念,所以人们经常用数学词汇介绍它,比如说“大O记法可用来描述一个函数的增长率的上限”,或者“如果函数g(x)的增长速度不比函数f(x)快,那么就称g属于O(f)”。大家数学背景不同,所以这些说法可能对你有意义,也可能没什么帮助。有了这本书,你不需要了解太多数学知识,就可以理解大O。
常数时间与线性时间
从O(N)可以看出,大O记法不只是用固定的数字(如22、440)来表示算法的步数,而是基于要处理的数据量来描述算法所需的步数。或者说,大O解答的是这样的问题:当数据增长时,步数如何变化?
O(N)算法所需的步数等于数据量,意思是当数组增加一个元素时,O(N)算法就要增加1步。而O(1)算法无论面对多大的数组,其步数都不变。
下图展示了这两种时间复杂度。
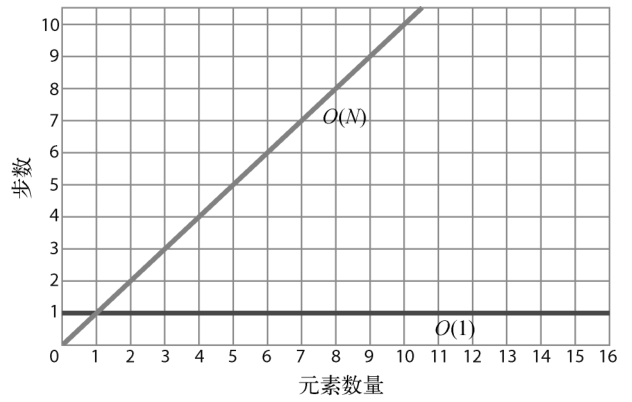
从图中可以看出,O(N)呈现为一条对角线。当数据增加一个单位时,算法也随之增加一步。也就是说,数据越多,算法所需的步数就越多。O(N)也被称为线性时间。
相比之下,O(1)则为一条水平线,因为不管数据量是多少,算法的步数都恒定。所以,O(1)也被称为常数时间。
因为大O主要关注的是数据量变动时算法的性能变化,所以你会发现,即使一个算法的恒定步数不是1,它也可以被归类为O(1)。假设有个算法不能1步完成,而要花3步,但无论数据量多大,它都需要3步。如果用图形来展示,该算法应该是这样:
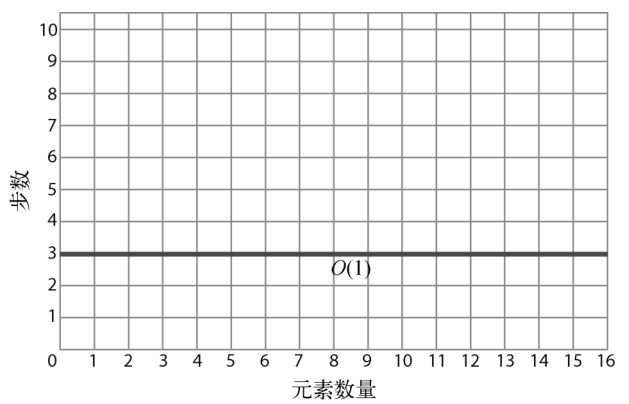
因为不管数据量怎样变化,算法的步数都恒定,所以这也是常数时间,也可以表示为O(1)。虽然从技术上来说它需要3步而不是1步,但大O记法并不纠结于此。简单来说,O(1)就是用来表示所有数据增长但步数不变的算法。
如果说只要步数恒定,3步的算法也属于O(1),那么恒为100步的算法也属于O(1)。虽然100步的算法在效率上不如1步的算法,但如果它的步数是恒定的,那么它还是比O(N)更高效。
为什么呢?如图所示。
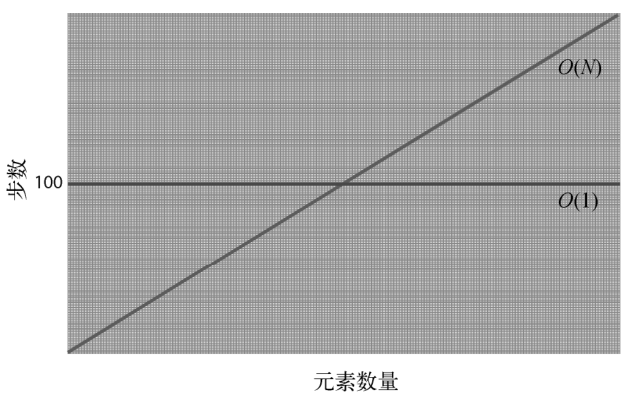
对于元素量少于100的数组,O(N)算法的步数会少于100步的O(1)算法。当元素刚好为100个时,两者的步数同为100。而一旦超过100个元素,注意,O(N)的步数就多于O(1)。
因为数据量从这个临界点开始,直至无限,O(N)都会比O(1)花更多步数,所以总体上来说,O(N)比O(1)低效。
这对于步数恒为1000000的O(1)算法来说也是一样的。当数据量一直增长时,一定会到达一个临界点,使得O(N)算法比O(1)算法低效,而且这种落后的状况会持续到数据量无限大的时候。
同一算法,不同场景
之前的章节我们提到,线性查找并不总是O(N)的。当要找的元素在数组末尾,那确实是O(N)。但如果它在数组开头,1步就能找到的话,那么技术上来说应该是O(1)。所以概括来说,线性查找的最好情况是O(1),最坏情况是 O(N)。
虽然大O可以用来表示给定算法的最好和最坏的情景,但若无特别说明,大O记法一般都是指最坏情况。因此尽管线性查找有O(1)的最好情况,但大多数资料还是把它归类为O(N)。
这种悲观主义其实是很有用的:知道各种算法会差到什么程度,能使我们做好最坏打算,以选出最适合的算法。
第三种算法
上一章我们学到:在同一个有序数组里,二分查找比线性查找要快。下面就来看看如何用大O记法描述二分查找。
它不能写成O(1),因为二分查找的步数会随着数据量的增长而增长。它也不能写成O(N),因为步数比元素数量要少得多,正如之前我们看到的,包含100个元素的数组只要7步就能找完。
看来,二分查找的时间复杂度介于O(1)和O(N)之间。
好了,二分查找的大O记法是:
我将其读作“O log N”。归于此类的算法,它们的时间复杂度都叫作对数时间。
简单来说,O(log N)意味着该算法当数据量翻倍时,步数加1。这确实符合之前章节我们所介绍的二分查找。下面我们先整理一下至今学到的东西,之后马上就解释采取这种记法的原因。
到这里我们所提过的3种时间复杂度,按照效率由高到低来排序的话,会是这样:
- O(1)
- O(log N)
- O(N)
下图为它们三者的对比。
注意O(log N)曲线的微弯,使其效率略差于O(1),却远胜于O(N)。
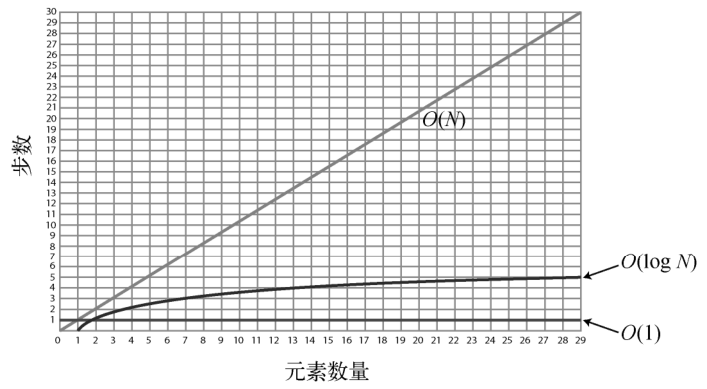
若想理解这种时间复杂度为什么是O(log N),我们得先学习一下对数。如果你对这个数学概念已经很熟悉了,那么可以跳过下一节。
对数
让我们来研究下为什么二分查找之类的算法被记为O(log N),到底log是什么?
log即是对数(logarithm)。注意,虽然它的英文看起来和读起来都跟算法(algorithm)很像,但它与算法无关。
对数是指数的反函数,所以我们先回顾一下指数。
23等于:1
2 × 2 × 2
结果为8。
log28 则将上述计算反过来,它意思是:要把2乘以自身多少次,才能得到8。因为需要3次,所以,log28 = 3。
再来一个例子。
26可以解释为:1
2 × 2 × 2 × 2 × 2 × 2 = 64
因为2要乘以自身6次才得到64,所以,log264 = 6。
不过以上都是教科书式的定义,我打算换一种更形象和更易于理解的方式来解释。
log2 8可以表达为:将8不断地除以2直到1,需要多少个2。
(注:按照从左到右的顺序计算。)
1 | 8 / 2 / 2 / 2 = 1 |
或者说,将8不断地除以2,要除多少次才能到1呢?答案是3,所以,log28 = 3。
类似地,log264可以解释为:将64除以2多少次,才能得到1。
1 | 64 / 2 / 2 / 2 / 2 / 2 / 2 = 1 |
因为这里有6个2,所以,log264 = 6。
现在你应该明白对数是怎么回事了,那么O(log N)就很好懂了。
解释O(log N)
现在回到大O记法。当我们说O(log N)时,其实指的是O(log2N),不过为了方便就省略了2而已。
你应该还记得O(N)代表算法处理N个元素需要N步。如果元素有8个,那么这种算法就需要8步。
O(log N)则代表算法处理N个元素需要log2N步。如果有8个元素,那么这种算法需要3步,因为log28 = 3。
从另一个角度来看,如果要把8个元素不断地分成两半,那么得拆分3次才能拆到只剩1个元素。
这正是二分查找所干的事情。它就是不断地将数组拆成两半,直至范围缩小到只剩你要找的那个元素。
简单来说,O(log N)算法的步数等于二分数据直至元素剩余1个的次数。
下表是O(N)和O(log N)的效率对比。
| 8 | 8 | 3 |
| 16 | 16 | 4 |
| 32 | 32 | 5 |
| 64 | 64 | 6 |
| 128 | 128 | 7 |
| 256 | 256 | 8 |
| 512 | 512 | 9 |
| 1024 | 1024 | 10 |
每次数据量翻倍时,O(N)算法的步数也跟着翻倍,O(log N)算法却只需加 1。
后面的章节我们还会学到除了这3种时间复杂度以外的算法。不过现在,我们还是先把已经学会的实践到日常的代码中。
实例
以下是打印列表所有元素的典型Python代码。1
2
3things = ['apples', 'baboons', 'cribs', 'dulcimers']
for thing in things:
print "Here's a thing: %s" % thing
它的效率要怎么用大O记法来表示呢?
首先,这是一个算法的例子。虽然它并没有多么厉害,但不管一段代码做什么事情,技术上来说它都是一个算法--因为它是解决某种问题的一个独特的过程。在此例中,问题是打印列表的所有元素,而算法是在for循环中使用print 。
为了得出它的大O记法,我们需要分析这个算法的步数。这段代码的主要部分--for循环会走4步,因为列表总共有4个元素。
然而,此过程不一定总是这样。如果列表有10个元素,那么for循环就会是10步。因为这里for的步数等于元素数量,所以整个算法的效率是O(N)。
再来一个例子,这是大家都知道的最基础的代码。1
print('Hello world!')
它永远都只会是1步,所以是O(1)。
以下的例子是代码判断一个数字是否为质数。1
2
3
4
5def is_prime(number):
for i in range(2, number):
if number % i == 0:
return False
return True
它接受一个参数,名为number ,然后用一个for 循环来测试number除以2到number之间的数,看是否有余数。如果没有,则number非质数,可以马上返回False。但如果一直测到number除以number的前一个数都有余数,那么它就是一个质数,最后会返回True。
此算法的效率为O(N)。它不以数组为参数,而是用一个数字。如果is_prime传入的是7,那么for循环就要差不多走7次(准确来说是5步,因为是从2开始,直到该数字的前一个数)。如果是101,那就循环差不多101次。因为步数与参数的大小一致,所以它的效率是O(N)。
总结
学会大O记法,我们在比较算法时就有了一致的参考系。有了它,我们就可以在现实场景中测量各种数据结构和算法,写出更快的代码,更轻松地应对高负荷的环境。
下一章会用一个实际的例子,让你看到大O记法如何帮助我们显著地提高代码的性能。