思考并回答以下问题:
- 冒泡排序为什么叫冒泡排序?冒泡排序的大O记法是什么?为什么?
- 冒泡排序的执行步骤是哪两步?图是什么样的?也叫作什么?
- 嵌套循环算法的效率是怎么样的?
- 检查数组中是否有重复值怎么进行线性解决?
本章涵盖:
- 冒泡排序
- 冒泡排序实战
- 冒泡排序的实现
- 冒泡排序的效率
- 二次问题
- 线性解决
大O记法能客观地衡量各种算法的时间复杂度,是比较算法的利器。我们也试过用它来对比二分查找和线性查找的步数差异,发现二分查找的步数为O(log N),比线性查找的O(N)快得多。
然而,写代码的时候并不总有这样明确的二选一,更多时候你可能就直接采用首先想到的那种算法了。不过有了大O的话,你就可以与其他常用的算法比较,然后问自己:“我的算法跟它们相比,是快还是慢?”
如果你通过大O发现自己的算法比其他的要慢,你就应该退一步,好好想想怎样优化它,才能使它变成更快的那种大O。虽然并不总有提升空间,但在确定编码之前多加考虑还是好的。
本章我们会写些代码来解决一个实际问题,并且会用大O来测量算法的性能,然后看看是否能对算法做些修改,使得性能提升。(剧透:能。)
冒泡排序
但在讨论实际问题之前,先来学习一种新的时间复杂度。我们会从计算机科学的经典算法之一开始阐述。
排序算法是计算机科学中被广泛研究的一个课题。历时多年,它发展出了数十种算法,这些算法都着眼于一个问题:
如何将一个无序的数字数组整理成升序?
你会在本章以及下一章看到这些算法。起初我们会学习一些“简单排序”,它们很好懂,但效率不如其他排序算法。
冒泡排序是一种很基本的排序算法,步骤如下。
(1)指向数组中两个相邻的元素(最开始是数组的头两个元素),比较它们的大小。
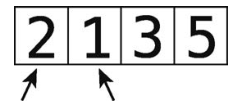
(2)如果它们的顺序错了(即左边的值大于右边),就互换位置。
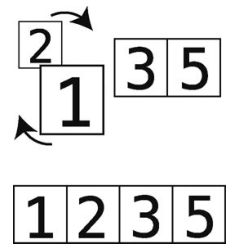
如果顺序已经是正确的,那这一步就什么都不用做。
(3)将两个指针右移一格。
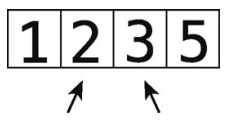
重复第(1)步和第(2)步,直至指针到达数组末尾。
(4)重复第(1)至(3)步,直至从头到尾都无须再做交换,这时数组就排好序了。
这里被重复的第(1)至(3)步是一个轮回,也就是说,这个算法的主要步骤被“轮回”执行,直到整个数组的顺序正确。
冒泡排序实战
下面来举一个完整的例子。假设要对[4, 2, 7, 1, 3]进行排序。它现在是无序的,我们的目标是产生一个包含相同元素、升序的数组。
开始第1次轮回。
数组一开始如下图所示。

第1步:首先,比较4和2。如图可见它们的顺序是错的。
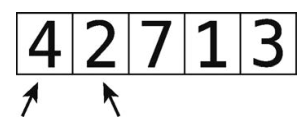
第2步:交换它们的位置。
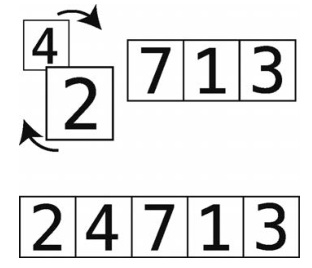
第3步:比较4和7。
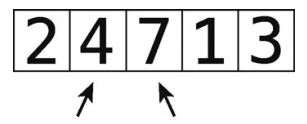
它们的顺序正确,所以不用做什么交换。
第4步:比较7和1。
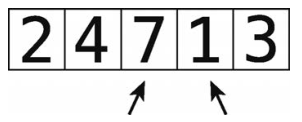
第5步:顺序错误,于是进行交换。
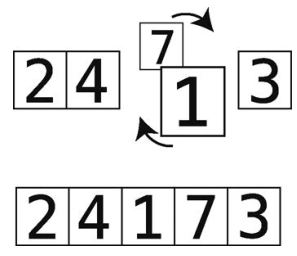
第6步:比较7和3。
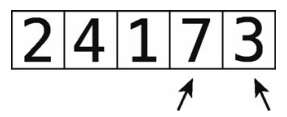
第7步:顺序错误,于是进行交换。
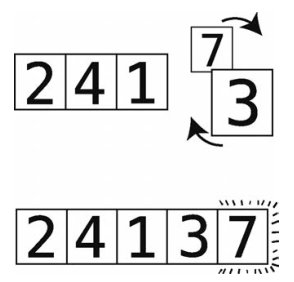
因为我们一直把较大的元素换到右边,所以现在最右侧的7正处于其正确位置上。我将那个格子用虚线圈起来了。
这也正是此种算法名为冒泡排序的原因:每一次轮回过后,未排序的值中最大的那个都会“冒”到正确的位置上。
因为刚才那次轮回做了不止一次的交换,所以得继续轮回。
下面来第2次轮回。
此时7已经在正确的位置上了。

第8步:从比较2和4开始。
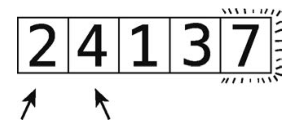
它们已经按顺序排好了,所以直接进行下一步。
第9步:比较4和1。
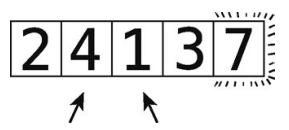
第10步:它们的顺序错误,于是交换。
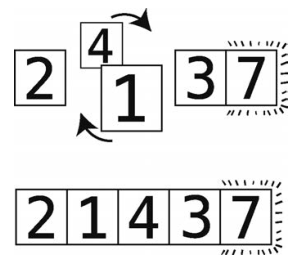
第11步:比较4和3。
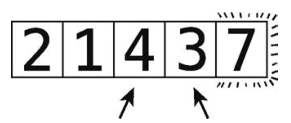
第12步:顺序错误,进行交换。
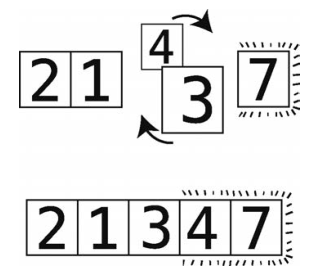
因为7已经在上一次轮回里排好了,所以无须比较4和7。此外,4移到了正确的位置,本次轮回结束。因为这次轮回也做了不止一次的交换,所以得继续轮回。
下面来第3次轮回。
第13步:比较2和1。
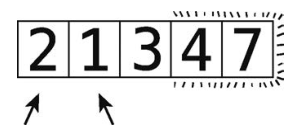
第14步:顺序错误,进行交换。
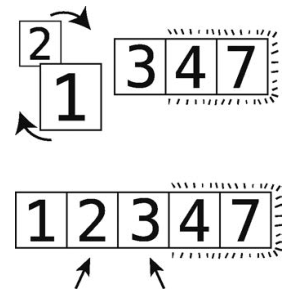
第15步:比较2和3。

顺序正确,不用交换。
这时3也“冒”到其正确位置了。因为这次轮回做了不止一次的交换,所以还要继续。
于是开始第4次轮回。
第 16步:比较1和2。
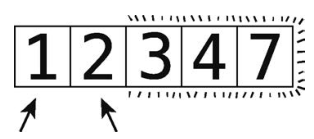
顺序正确,不用交换。而且剩下的元素也都排好序了,轮回结束。
因为刚才的轮回没有任何交换,可知整个数组都已排好序。

冒泡排序的实现
以下是用Python写的冒泡排序。1
2
3
4
5
6
7
8
9
10
11
12
13
14def bubble_sort(list):
unsorted_until_index = len(list) - 1
sorted = False
while not sorted:
sorted = True
for i in range(unsorted_until_index):
if list[i] > list[i+1]:
sorted = False
list[i], list[i+1] = list[i+1], list[i]
unsorted_until_index = unsorted_until_index - 1
list = [65, 55, 45, 35, 25, 15, 10]
bubble_sort(list)
print list
让我们来一行行地分析。我会先摘出代码片段,然后给出解释。1
unsorted_until_index = len(list) - 1
变量unsorted_until_index表示“该索引之前的数据都没排过序”。一开始整个数组都是没排过序的,所以此变量赋值为数组的最后一个索引。1
sorted = False
另外还有一个sorted变量,被用来记录数组是否已完全排好序。当然一开始它应该是False 。1
2while not sorted:
sorted = True
接着是一个while循环,除非数组排好了序,不然它不会停下来。然后,我们先将sorted初步设置为True。当发生任何交换时,我们会将其改为False。如果在一次轮回里没有做过交换,那么sorted就确定为True,我们知道数组已排好序了。1
2
3
4for i in range(unsorted_until_index):
if list[i] > list[i+1]:
sorted = False
list[i], list[i+1] = list[i+1], list[i]
在while循环里,还有一个for循环会迭代未排序元素的索引值。此循环中,我们会比较相邻的元素,如果有顺序错误,就会进行交换,并将sorted改为False 。1
unsorted_until_index = unsorted_until_index - 1
到了这一行,就意味着一次轮回结束了,同时该次轮回中冒泡到右侧的值处于正确位置。因为unsorted_until_index所指的位置已放上了正确的元素,所以减1,以便下一次轮回能略过该位置。
一次while 循环就是一次轮回,循环会持续直至sorted确定为True 。
冒泡排序的效率
冒泡排序的执行步骤可分为两种。
- 比较:比较两个数看哪个更大。
- 交换:交换两个数的位置以使它们按顺序排列。
先看看冒泡排序要进行多少次比较。
回顾之前那个5个元素的数组,你会发现在第1次轮回我们为4对元素进行了4次比较。
到了第2次轮回,则只做了3次比较。这是因为第1次轮回已经确定了最后一个格子的元素,所以不用再比较最后两个元素了。
第3次轮回,只比较2次;第4次,只比较1次。
算起来就是:
4 + 3 + 2 + 1 = 10 次比较。
推广到N个元素,需要
(N - 1) + (N - 2) + (N - 3) + … + 1次比较。
分析过比较之后,再来看看交换。
如果数组不只是随机打乱,而是完全反序,在这种最坏的情况下,每次比较过后都得进行一次交换。因此10次比较加10次交换,总共20步。
现在把两种步骤放在一起来看。一个含有10个元素的数组,需要:
9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45次比较,以及45次交换,共90步。
20个元素的话,就是:
19 + 18 + 17 + 16 + 15 + 14 + 13 + 12 + 11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 190次比较,以及190次交换,共380步。
效率太低了。元素量呈倍数增长,步数却呈指数增长,如下表所示。
| 5 | 20 |
| 10 | 90 |
| 20 | 380 |
| 40 | 1560 |
| 80 | 6320 |
再看仔细一点,你会发现随着N的增长,步数大约增长为N2 。
| 5 | 20 | 25 |
| 10 | 90 | 100 |
| 20 | 380 | 400 |
| 40 | 1560 | 1600 |
| 80 | 6320 | 6400 |
因此描述冒泡排序效率的大O记法,是O(N2)。
规范一些来说:用O(N2)算法处理N个元素,大约需要N2步。
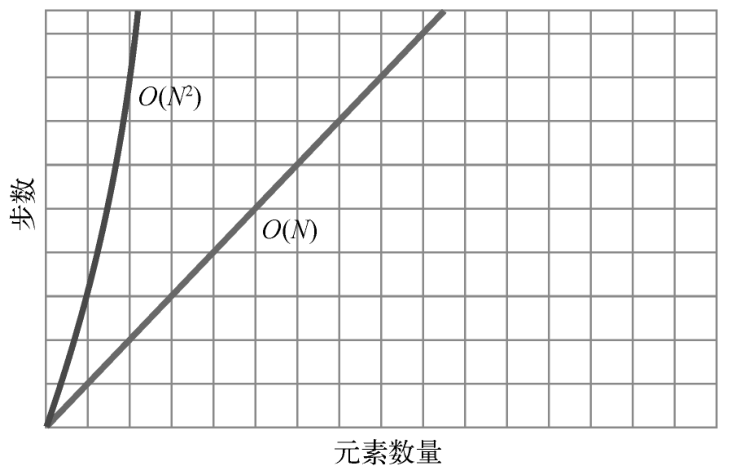
O(N2)算法是比较低效的,随着数据量变多,其步数也剧增,如下图所示。
注意O(N2)代表步数的曲线非常陡峭,O(N)的则只呈对角线状。
最后一点:O(N2)也被叫作二次时间。
二次问题
假设你正在写一个JavaScript应用,它要检查数组中是否有重复值。
首先想到的做法可能是类似下面的嵌套for循环。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15function hasDuplicateValue(array)
{
for(var i = 0; i < array.length; i++)
{
for(var j = 0; j < array.length; j++)
{
if(i !== j && array[i] == array[j])
{
return true;
}
}
}
return false;
}
此函数用var i来遍历数组元素。每当i指向下一元素时,我们又发起第二个for循环,用var j来遍历数组元素,并在这第二个循环过程中检查i和j两个位置的值是否相同。若相同,则表示数组有重复值。如果两层循环都没遇到重复值,则最终返回false,以示数组没有重复值。
虽然可以这么做,但它的效率高吗?既然我们学过一点大O记法,那么就试试用大O来评价一下这个函数吧。
记住,大O测量的是步数与数据量的关系。因此,我们要测的就是:给hasDuplicateValue函数传入一个含有N个元素的数组,最坏情况下需要多少步才能完成。
要回答这个问题,得先搞清楚这个函数有哪些步骤,以及其最坏情况是什么。
该函数只有一种步骤,就是比较。它重复地比较i和j所指的值,看它们是否相等,以判断数组有没有重复值。最坏的情况就是没有重复,这将使我们跑遍内外两层循环,比较完所有i、j组合,才返回false 。
由此可知N个元素要比较N2次。因为外层循环需要N步来遍历数组,而这里的每1步,又会发起内层循环去用N步遍历数组。所以N步乘以N步等于N2步,此函数为一个O(N2)算法。
想要证明的话,还可以往函数里添加一些跟踪步数的代码。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19function hasDuplicateValue(array)
{
var steps = 0;
for(var i = 0; i < array.length; i++)
{
for(var j = 0; j < array.length; j++)
{
steps++;
if(i !== j && array[i] == array[j])
{
return true;
}
}
}
console.log(steps);
return false;
}
执行hasDuplicateValue([1,2,3])的话,你会看到Javascript console输出9,表示9次比较。3个元素需要9次比较,这个函数是O(N2)的经典例子。
毫无疑问,嵌套循环算法的效率就是O(N2)。一旦看到嵌套循环,你就应该马上想到O(N2)。
虽然hasDuplicateValue是我们目前唯一想到的解决方法,但在确定采用之前,应意识到它的O(N2)意味着低效。当遇到低效的算法时,我们都应该花些时间思考下有没有更快的做法。
特别是当数据量巨大的时候,优化不足的应用甚至可能会突然挂掉。尽管这可能已经是最佳方案,但你还是要确认一下。
线性解决
以下是hasDuplicateValue的另一种实现,它没有嵌套循环。看看它是否会比之前的更加高效。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17function hasDuplicateValue(array)
{
var existingNumbers = [];
for(var i = 0; i < array.length; i++)
{
if(existingNumbers[array[i]] === undefined)
{
existingNumbers[array[i]] = 1;
}
else
{
return true;
}
}
return false;
}
此实现只有一个循环,并将迭代过程中遇到的数字用数组existingNumbers记录下来。其记录方法很有趣:每发现一个新的数字,就以其为索引找出existingNumbers中对应的格子,将其赋值为1。
举个例子,如果参数array为[3,5,8],那么循环结束时,existingNumbers就会变成以下这样。1
[undefined, undefined, undefined, 1, undefined, 1, undefined, undefined, 1] // 第一次索引为3,5,8的时候和undefined比较是相等的,所以赋值为1。0,1,2,4等索引没有赋值,所以是undefined
里面那些1的位置为索引3、5、8,因为array包含的这些数字已被发现。
不过,在将1赋值到对应的索引上之前,还得先检查索引上是否已有1。如果有,那就意味着这个数字曾经遇到过,也就是传入的数组有重复值。
为了确定这一新算法的时间复杂度符合哪种大O,我们得考察其最坏情况下需要多少步。与上一算法类似,此算法的主要步骤也是比较。读取existingNumbers上某索引的值,并与undefined比较,代码如下。1
if(existingNumbers[array[i]] === undefined)
(其实除了比较,我们还要对existingNumbers进行插入,但这无关紧要,原因会在下一章进行讲解。)
同样,最坏的情况就是无重复,因为你得跑完整个循环才能发现。
可见N个元素就要N次比较。因为这里只有一个循环,数组有多少个元素,它就要迭代多少次。要证明这个猜想,可以用JavaScript console来打印步数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22function hasDuplicateValue(array)
{
var steps = 0;
var existingNumbers = [];
for(var i = 0; i < array.length; i++)
{
steps++;
if(existingNumbers[array[i]] === undefined)
{
existingNumbers[array[i]] = 1;
}
else
{
return true;
}
}
console.log(steps);
return false;
}
执行hasDuplicateValue([1,2,3])的话,你会看到输出为3,跟元素个数一致。
因此其大O记法是O(N)。
我们知道O(N)远远快于O(N2),所以采用第二种算法能极大地提升hasDuplicateValue的效率。如果这个程序处理的数据量很大,那么性能差别是很明显的(其实第二种算法有一个缺点,不过我们在最后一章才会讲到)。
总结
毫无疑问,熟悉大O记法能使我们发现低效的代码,有助于我们挑选出更快的算法。然而,偶尔也会有两种算法的大O相同,但实际上二者快慢不一的情况。下一章我们就来学习当大O记法太过粗略的时候,如何识别两种算法的效率高低。