思考并回答以下问题:
- 插入排序的第二层为什么是while循环?
- 插入排序包含4种步骤:移除、比较、平移和插入。各需要多少步?
- 用Python和C#实现插入排序。
- 冒泡排序、选择排序、插入排序都需要双循环吗?
本章涵盖:
- 插入排序
- 插入排序实战
- 插入排序的实现
- 插入排序的效率
- 平均情况
之前我们衡量一个算法的效率时,都是着眼于它在最坏情况下需要多少步。原因很简单,连最坏的情况都做足准备了,其他情况自然不在话下。
然而,本章会告诉你最坏情况不是唯一值得考虑的情况。全面分析各种情况,能帮助你为不同场景选择适当的算法。
插入排序
我们已经学过两种排序算法:冒泡排序和选择排序。虽然它们的效率都是O(N2),但其实选择排序比冒泡排序快一倍。现在来学第三种排序算法--插入排序。你会发现,顾及最坏情况以外的场景将是多么有用。
插入排序包括以下步骤。
(1)在第一轮里,暂时将索引1(第2格)的值移走,并用一个临时变量来保存它。这使得该索引处留下一个空隙,因为它不包含值。
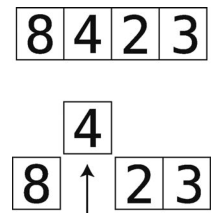
在之后的轮回,我们会移走后面索引的值。
(2)接着便是平移阶段,我们会拿空隙左侧的每一个值与临时变量的值进行比较。
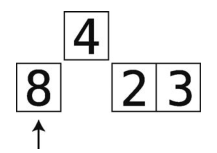
如果空隙左侧的值大于临时变量的值,则将该值右移一格。
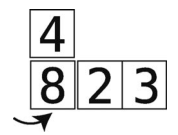
随着值右移,空隙会左移。如果遇到比临时变量小的值,或者空隙已经到了数组的最左端,就结束平移阶段。
(3)将临时移走的值插入当前空隙。
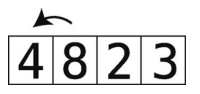
(4)重复第(1)至(3)步,直至数组完全有序。
插入排序实战
下面尝试对[4, 2, 7, 1, 3]数组运用插入排序。
第1轮先从索引1开始,其值为2。
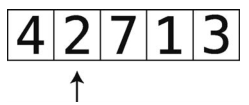
准备工作:暂时移走2,并将其保存在变量temp_value中。图中被移到数组上方的就是temp_value。
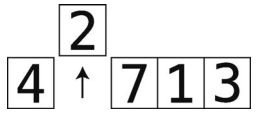
第1步:比较4与temp_value中的2。
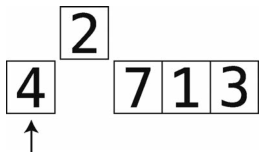
第2步:因为4大于2,所以把4右移。
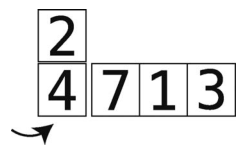
于是空隙移到了数组最左端,没有其他值可以比较了。
第3步:将temp_value插回数组,完成第一轮。
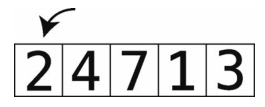
开始第2轮。
准备工作:暂时移走索引2的值,并保存到temp_value中。于是temp_value等于7。
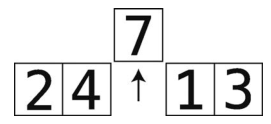
第4步:比较4与temp_value 。
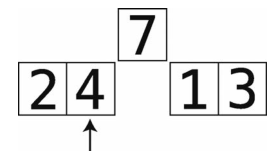
4小于7,所以无须平移。因为遇到了小于temp_value的值,所以平移阶段直接结束。
第5步:将temp_value插回到空隙中,结束第2轮。
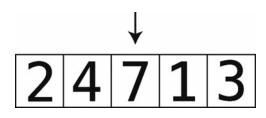
开始第3轮。
准备工作:暂时移走1,并将其保存到temp_value中。
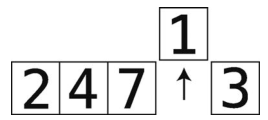
第6步:比较7与temp_value。
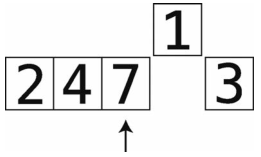
第7步:7大于1,于是将7右移。
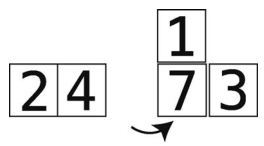
第8步:比较4与temp_value。
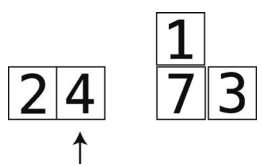
第9步:4大于1,于是也要将4右移。
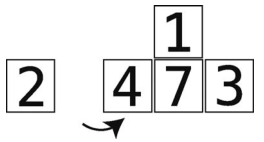
第10步:比较2与temp_value。
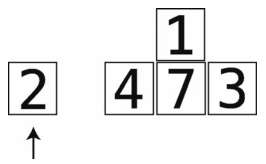
第11步:2比较大,所以将2右移。
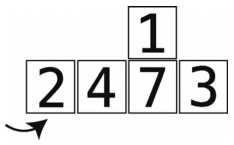
第12步:空隙到了数组最左端,因此我们将temp_value插进去,结束这一轮。
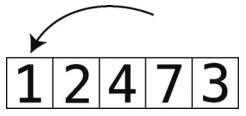
开始第4轮。
准备工作:暂时移走索引4的值3,保存到temp_value中。
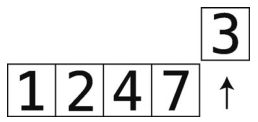
第13步:比较7和temp_value。
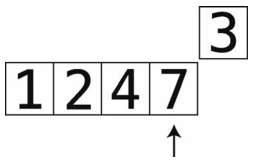
第14步:7更大,于是将7右移。
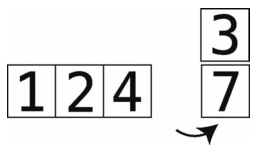
第15步:比较4与temp_value 。
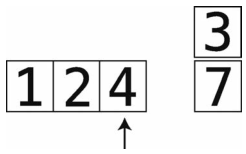
第16步:4大于3,所以将4右移。
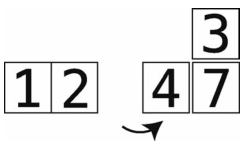
第17步:比较2与temp_value。2小于3,于是平移阶段完成。
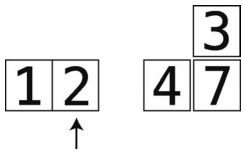
第18步:把temp_value插回到空隙。
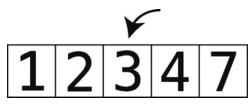
至此整个数组都排好序了。

插入排序的实现
以下是插入排序的Python实现。1
2
3
4
5
6
7
8
9
10def insertion_sort(array):
for index in range(1, len(array)):
position = index
temp_value = array[index]
while position > 0 and array[position - 1] > temp_value:
array[position] = array[position - 1]
position = position - 1
array[position] = temp_value
让我们来一步步地讲解。我会先摘出代码片段,然后给出解释。1
for index in range(1, len(array)):
首先,发起一个从索引1开始的循环来遍历数组。变量 index保存的是当前索引。1
2position = index
temp_value = array[index]
接着,给position赋值为index,给temp_value赋值为index所指的值。1
2
3while position > 0 and array[position - 1] > temp_value:
array[position] = array[position - 1]
position = position - 1
然后在内部发起一个while循环,以检查position左侧的值是否大于temp_value。若是,则用array[position] = array[position - 1]将该值右移一格,并将position减1。然后继续检查新position左侧的值是否大于temp_value……如此重复,直至遇到的值比temp_value小。1
array[position] = temp_value
最后,将temp_value放回到数组的空隙中。
插入排序的效率
插入排序包含4种步骤:移除、比较、平移和插入。要分析插入算法的效率,就得把每种步骤都统计一遍。
首先看看比较。每次拿temp_value跟空隙左侧的值比大小就是比较。
在数组完全逆序的最坏情况下,我们每一轮都要将temp_value左侧的所有值与temp_value比较。因为那些值全都大于temp_value,所以每一轮都要等到空隙移到最左端才能结束。
在第一轮,temp_value为索引1的值,由于temp_value左侧只有一个值,所以最多进行一次比较。到了第二轮,最多进行两次比较,以此类推。到最后一轮时,就要拿temp_value以外的所有值与其进行比较。换言之,如果数组有N个元素,则最后一轮中最多进行N - 1次比较。
因而可以得出比较的总次数为:
1 + 2 + 3 + … + N - 1次。
对于有 5个元素的数组,最多需要:
1 + 2 + 3 + 4 = 10次比较。
对于有 10个元素的数组,最多需要:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45次比较。
(对于有20个元素的数组,最多需要190次比较,以此类推。)
由此可发现一个规律:对于有N个元素的数组,大约需要N2/2次比较(102/2是50,202/2是200)。
接下来看看其他几种步骤。
我们每次将值右移一格,就是平移操作。当数组完全逆序时,有多少次比较就要多少次平移,因为每次比较的结果都会使你将值右移。
把最坏情况下的比较步数和平移步数相加。
N2/2次比较 + N2/2次平移 = N2步
temp_value的移除跟插入在每一轮里都会各发生一次。因为总是有N - 1轮,所以可以得出结论:有N - 1次移除和N - 1次插入。
把它们都相加。
N2比较和平移的合计 + N - 1次移除 + N - 1次插入 = N2 + 2N - 2步
我们已经知道大O有一条重要规则--忽略常数,于是你可能会将其简化成O(N2 + N)。
不过,现在来学习一下大O的另一条重要规则:
大O只保留最高阶的N。
换句话说,如果有个算法需要N4 + N3 + N2 + N步,我们就只会关注其中的N4,即以O(N4)来表示。为什么呢?
请看下表。
| N | N2 | N3 | N4 |
|---|---|---|---|
| 2 | 4 | 8 | 16 |
| 5 | 25 | 125 | 625 |
| 10 | 100 | 1000 | 10000 |
| 100 | 10000 | 1000000 | 1000000000 |
| 1000 | 1000000 | 1000000000 | 1000000000000 |
随着N的变大,N4的增长越来越抛离其他阶。当N为1000时,N4就比N3大了1000倍。因此,我们只关心最高阶的N。
所以在插入排序的例子中,O(N2 + N)还得进一步简化成O(N2)。
你会发现,在最坏的情况里,插入排序的时间复杂度跟冒泡排序、选择排序一样,都是O(N2)。
不过上一章曾指出,虽然冒泡排序和选择排序都是O(N2),但选择排序实际上是N2/2步,比N2步的冒泡排序更快。乍一看,你可能会觉得插入排序跟冒泡排序一样,因为它们都是O(N2),其实插入排序是N2 + 2N - 2步。
如果本书到此为止,你或许会认为比冒泡排序和插入排序快一倍的选择排序是三者中最优的,但事情并没有这么简单。
平均情况
确实,在最坏情况里,选择排序比插入排序快。但是我们还应该考虑平均情况。
为什么呢?
所谓平均情况,就是那些最常遇见的情况。最坏情况和最好情况都是不常见的。看下面这个钟形的曲线。
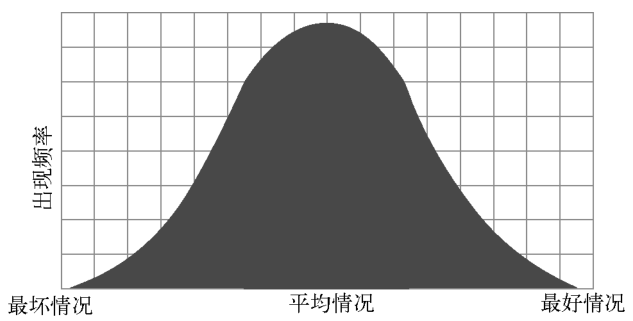
最好情况和最坏情况很少发生。现实世界里,最常出现的是平均情况。
这是很有道理的。你设想一个随便洗乱的数组,出现完全升序或完全降序的可能性有多大?
最可能出现的情况应该是随机分布。
下面试试在各种场景中测试插入排序。
完全降序的最坏情况之前已经见过,它每一轮都要比较和平移所遇到的值(这两种操作合计N2步)。
对于完全升序的最好情况,因为所有值都已在其正确的位置上,所以每一轮只需要一次比较,完全不用平移。
但若是随机分布的数组,你就可能要在一轮里进行比较并平移所有数据、部分数据,或无须平移。回头看看之前步骤分解的例子,可以发现在第 1、3轮,我们比较并平移了所有遇到的数据。在第4轮,我们只对部分数据进行了操作。在第2轮,则没有平移,只有一次比较。
最坏情况是所有数据都要比较和平移;最好情况是每轮一次比较、零次平移;对于平均情况,总的来看,是比较和平移一半的数据。
如果说插入排序的最坏情况需要N2步,那么平均情况就是N2/2步。尽管最终大O都会写成O(N2)。
来看一些具体的例子。
最好情况就像[1 ,2, 3, 4],已经预先排好序。用同样的数据,最坏情况就是[4, 3, 2, 1] 。
平均情况,则如[1, 3, 4, 2] 。
这里的最坏情况需要6次比较和6次平移,共12步。平均情况需要4次比较和2次平移,共6步。最好情况是3次比较、0次平移。
可以看到插入排序的性能在不同场景中差异很大。最坏、平均、最好情况,分别需要N2、N2/2、N步。
这是由于有些轮次需要比较temp_value左侧的所有值,有些轮次却因为遇到了小于temp_value的值而提早结束。
3种情况的步数如下图所示。
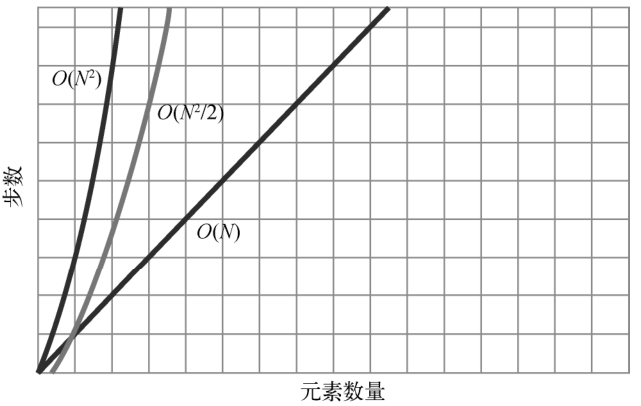
再跟选择排序对比一下。选择排序是无论何种情况,最坏、平均、最好,都要N2/2步。
因为这个算法没有提早结束某一轮的机制,不管遇到什么,每一轮都得比较所选索引右边的所有值。
那么哪种算法更好?选择排序还是插入排序?答案是:看情况。对于平均情况(数组里的值随机分布),它们性能相近。如果你确信数组是大致有序的,那么插入排序比较好。如果是大致逆序,则选择排序更快。如果你无法确定数据是什么样,那就算是平均情况了,两种都可以。
一个实例
假设你在写一个Javascript应用,你需要找出其中两个数组的交集。所谓交集,就是两个数组都有的值所组成的集合。举个例子,[3, 1, 4, 2]和[4, 5, 3, 6]的交集为[3, 4],因为两个数组都有3和4。
Javascript并没有自带求交集的函数,因此我们只能自己写一个。以下是其中一种写法。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17function intersection(first_array, second_array)
{
var result = [];
for (var i = 0; i < first_array.length; i++)
{
for (var j = 0; j < second_array.length; j++)
{
if (first_array[i] == second_array[j])
{
result.push(first_array[i]);
}
}
}
return result;
}
它运用了一个简单嵌套循环。外部循环用来遍历第一个数组,并在每遇到一个值时,就发起内部循环去检查第二个数组有没有值与其相同。
此算法有两种步骤:比较和插入。也就是将两个数组的所有值相互比较,并把相同的值插入到result。插入的步数微不足道,因为即使两个数组完全一致,步数也不过是其中一个数组的数据量。所以这里主要考虑的是比较。
要是两个数组同样大小,那么比较需要N2步。这是因为数组一的每个值,都要与数组二的每个值进行对比。于是,两个数据量都为5的数组,最终会比较25次。这种算法效率为O(N 2)。
(如果数组大小不一,比如说分别含N、M个元素,那么此过程的步数就是O(N × M),但简单起见,就当它们大小一样吧。)
那能不能改进一下呢?
这就是为什么我们不能只考虑最坏情况的原因了。以现在的intersection函数的实现,无论遇到什么情况都是O(N2)的,不管你输入的两个数组完全不同还是完全相同。
如果两个数组真的没有交集,那你别无选择,只能检查完每个值才能确定。
但若是二者有交集,我们其实不用拿数组一的每个值去跟数组二的每个值对比。下面我就来解释为什么。
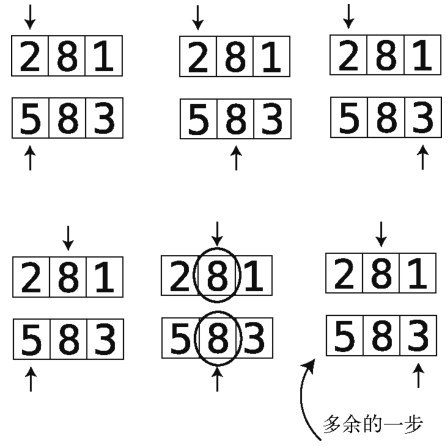
在以上例子中,一旦找到一个共有的值(8),那就没必要跑完内部循环了。再跑下去是为了检查什么呢?既然知道数组二中也存在数组一的那个值这就够了。
要改进的话,加一个命令就可以。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18function intersection(first_array, second_array)
{
var result = [];
for (var i = 0; i < first_array.length; i++)
{
for (var j = 0; j < second_array.length; j++)
{
if (first_array[i] == second_array[j])
{
result.push(first_array[i]);
break;
}
}
}
return result;
}
break可以中断内部循环,节省步数和时间。
这样的话,在没有交集的最坏情况下,我们仍然要做N2次比较;在数组完全一样的最好情况下,就只需要N次比较;在数组不同但有部分重复的平均情况下,步数会介于N到N2之间。
其性能提升是很明显的,因为在最初的实现里,无论什么情况,步数都是N2。
总结
懂得区分最好、平均、最坏情况,是为当前场景选择最优算法以及给现有算法调优以适应环境变化的关键。记住,虽然为最坏情况做好准备十分重要,但大部分时间我们面对的是平均情况。
下一章我们会学习一种跟数组类似的数据结构,它的一些特点使其在某些场景中的性能优于数组。就像现在你得根据需求选择合适的算法,数据结构的性能也有差异,你也需要为此做出选择。