思考并回答以下问题：

散列表是一种什么数据结构？优势在哪里？
为什么查找值只要一步？
什么是散列？什么是散列函数？
散列函数需要满足什么条件？
散列表是如何存储数据的？为什么会产生冲突？
分离链接法是怎么解决冲突的？
散列表的效率取决于什么因素？
什么是负载因子？理想的负载因子是多少？

本章涵盖：

探索散列表
用散列函数来做散列
一个好玩又赚钱的同义词典
处理冲突
找到平衡
一个实例
总结

试想你在写一个快餐店的点单程序，准备实现一个展示各种食物及相应价格的菜单。你可能会用数组来做（当然这没问题）。

1	menu = [ ["french fries", 0.75], ["hamburger", 2.5], ["hot dog", 1.5], ["soda", 0.6] ]

该数组由一些子数组构成，每个子数组包含两个元素。第一个元素是表示食物名称的字符串，第二个元素是该食物的价格。

就如第2章学到的，在无序的数组里查找某种食物的价格，得用线性查找，需要O(N)步。

有序数组则可以用二分查找，只需要O(log N)步。

尽管O(log N)也不错，但我们可以做得更好。事实上，可以好很多。到了本章结尾，你会掌握一种名为散列表的数据结构，只用O(1)步就能找出数据。理解此数据结构的原理以及其适用场景，你就能依靠其快速查找的能力来应对各种状况。

探索散列表

大多数编程语言都自带散列表这种能够快速读取的数据结构。但在不同的语言中，它有不同的名字，除了散列表，还有散列、映射、散列映射、字典、关联数组。散列就是hash。

以下便是用Ruby的散列表来实现的菜单。

1	menu = { "french fries" => 0.75, "hamburger" => 2.5, "hot dog" => 1.5, "soda" => 0.6 }

散列表由一对对的数据组成。一对数据里，一个叫作键，另一个叫作值。键和值应该具有某种意义上的关系。如上例，”french fries”是键，0.75是值，把它们组成一对就表示“炸薯条的价格为75美分”。

在Ruby中，查找一个键所对应的值，语法是：

1	menu["french fries"]

这会返回值0.75。

在散列表中查找值的平均效率为O(1)，因为只要一步。下面来看看为什么。

用散列函数来做散列

还记得你小时候创建和解析密文时用的密码吗？

例如以下这种字母和数字的简单转化方式。

A = 1
B = 2
C = 3
D = 4
E = 5

以此类推。

由此可得，ACE会转化为135，CAB会转化为312，DAB会转化为412，BAD会转化为214。

将字符串转为数字串的过程就是散列，其中用于对照的密码，就是散列函数。

当然散列函数不只是这一种，例如对各字母匹配的数字求和的过程，也可以作为散列函数。

按此函数来做的话，BAD就是7，过程如下。

第1步：BAD转成214。

第2步：把每一位数字相加，2 + 1 + 4 = 7。

散列函数也可以是对各字母匹配的数字求积的过程。这样的话，BAD就会得出8。

第1步：BAD转成214。

第2步：把每一位数字相乘，2 × 1 × 4 = 8。

本章剩余部分将会采用最后一种散列函数。虽然现实世界中的散列函数比这复杂得多，但以简单的乘法函数为例会比较易懂。

一个散列函数需满足以下条件才有效：每次对同一字符串调用该散列函数，返回的都应是同一数字串。如果每次都返回不一样的结果，那就无效。

例如，计算过程中使用随机数或当前时间的函数就不是有效的散列函数。这种函数会将BAD一下转成12，一下又转成106。

我们刚才的乘法函数就只会把BAD转成8。因为B总是2，A总是1，D总是4，2 × 1 × 4总会是8，不可能有其他输出。

注意，经由此函数转换，DAB也会得到8，跟BAD一样。这确实会带来一些问题，我们之后会说明。

认识了散列函数，就可以进一步学习散列表的运作了。

一个好玩又赚钱的同义词典

假设工作之余，你还一个人秘密研发着一款将要征服世界的软件。那是一个同义词典，它叫Quickasaurus。你相信它势必一鸣惊人，因为它只会返回一个最常用的同义词，而不是像其他词典那样，返回所有的同义词。

因为每个词都有一个同义词，所以正好作为散列表的用例。毕竟，散列表就是一堆成对的元素。下面我们马上来开发。

该词典可以用一个散列表来表示。

1	thesaurus = {}

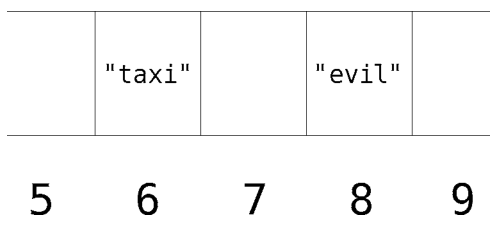
散列表可以看成是一行能够存储数据的格子，就像数组那样。每个格子都有对应的编号，如下所示。

现在往散列表里加入我们的第一条同义词。

1	thesaurus["bad"] = "evil"

散列表变成了下面这样。

1	{"bad" => "evil"}

再看看散列表是如何存储数据的。

首先，计算机用散列函数对键进行计算。为了方便演示，这里我们依然使用之前提及的那个乘法函数。

1	BAD = 2 * 1 * 4 = 8

“bad”的散列值为8，于是计算机将”evil”放到第8个格子里。

接着，我们再试另一对键值。

1	thesaurus["cab"] = "taxi"

同样地，计算机要计算散列值。

1	CAB = 3 * 1 * 2 = 6

因其结果为6，所以将”taxi”放到第6格。

再多加一对试试。

1	thesaurus["ace"] = "star"

ACE的散列值为15（ACE = 1 × 3 × 5 = 15），于是”star”被放到第15格。

现在，用代码来表示这个散列表的话，就是这样：

1	{"bad" => "evil", "cab" => "taxi", "ace" => "star"}

既然散列表词典建好了，那就来看看从里面查词时会发生什么吧。假设现在要查”bad”的同义词，写成代码的话，如下所示。

1	thesaurus["bad"]

收到命令后，计算机就会进行如下两步简单的操作。

(1)计算这个键的散列值：BAD = 2 × 1 × 4 = 8。

(2)由于结果是 8，因此去到第8格并返回其中的值。在本例中，该值为 “evil” 。

这下你应该明白为什么从散列表里读取数据只需O(1)了吧，因为其过程所花的时间是恒定的。它总是先计算出键的散列值，然后根据散列值跳到对应的格子去。

现在总算理解为什么我们的快餐店菜单用散列表会比用数组要快了。当要查询某种食物的价格时，如果是用数组，那么就得一个格子一个格子地去找，直至找到为止。无序数组需要O(N)，有序数组需要O(log N)。但用散列表的话，我们就能够以食物作为键来做O(1)的查找。这就是散列表的好处。

处理冲突

不过，散列表也会带来一些麻烦。

继续同义词典的例子：把下面这条同义词也加到表里，会发生什么呢？

1	thesaurus["dab"] = "pat"

首先，计算散列值。

1	DAB = 4 * 1 * 2 = 8

然后，将”pat”放进第8个格子。

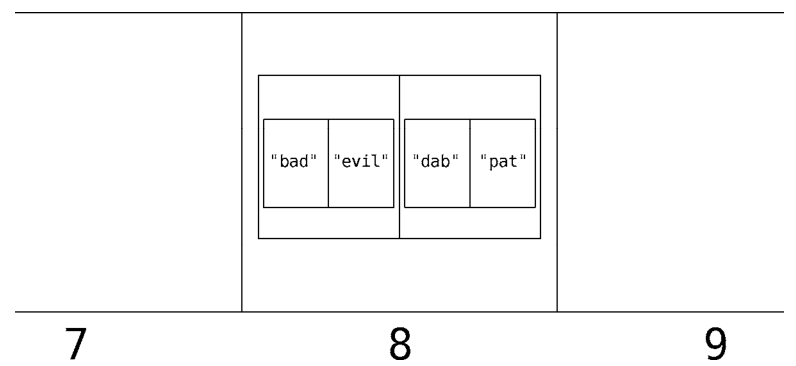
噢，第8格已经是”evil”了，这的确不好（evil）。

往已被占用的格子里放东西，会造成冲突。幸好，我们有解决办法。

一种经典的做法就是分离链接。当冲突发生时，我们不是将值放到格子里，而是放到该格子所关联的数组里。

现在仔细观察该散列表的冲突位置。

因为要放入”pat”的第8格，已经存在”evil”了，于是我们将第8格的内容换成一个数组。

该数组又以子数组构成，每个子数组含两个元素，第一个是被检索的词，后一个是其相应的同义词。

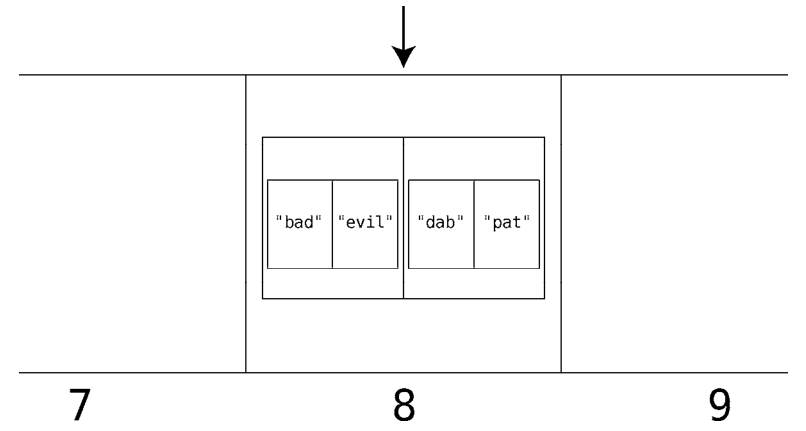
下面运行一遍”dab”的查找过程，执行：

1	thesaurus["dab"]

计算机就会按如下步骤执行。
(1)计算散列值DAB = 4 × 1 × 2 = 8。
(2)读取第8格，发现其中不是一个单独的值，而是一个数组。
(3)于是线性地在该数组中查找，检查每个子数组的索引0位置，如果碰到要找的词（”dab”），就返回该子数组的索引1的值。

再图形化地演示一次。

求得DAB的散列值为8，于是计算机读取第8格。

因为第8格里面是一个数组，所以对该数组进行线性查找。首先是第1格，它又是一个数组，于是查看这个子数组的索引0。

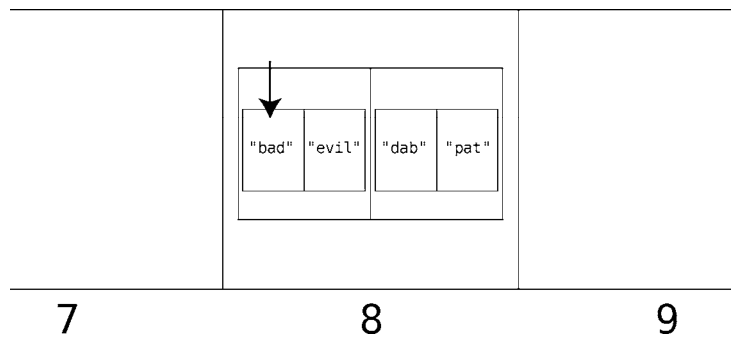
它并非我们要找的词（”dab”），于是跳到下一格。

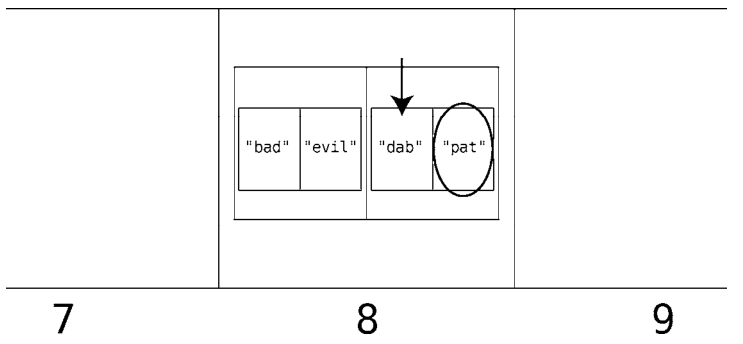
这一格的子数组的索引0正是”dab”，因此其索引1的值就是我们要找的同义词（”pat”）。

若散列表的格子含有数组，因为要在这些数组上做线性查找，所以步数会多于1。如果数据都刚好存在同一个格子里，那么查找就相当于在数组上进行。因此散列表的最坏情况就是O(N)。

为了避免这种情况，散列表的设计应该尽量减少冲突，以便查找都能以O(1)完成。

接着，我们就来看一下现实中的散列表是如何做到的。

找到平衡

归根到底，散列表的效率取决于以下因素。

要存多少数据。
有多少可用的格子。
用什么样的散列函数。

前两点很明显。如果要放的数据很多，格子却很少，就会造成大量冲突，导致效率降低。但为什么和散列函数本身也有关系呢？我们这就来看看。

假设你准备用一个散列值总是落在1至9之间的散列函数，例如，将字母转成其对应的序号，然后一直相加，直至结果只剩一位数字的函数。

就像这样：
PUT = 16 + 21 + 20 = 57
因为57不止一位数字，于是将57拆成5 + 7。
5 + 7 = 12
12也不止一位数字，于是拆成1 + 2。
1 + 2 = 3
最终，PUT的散列值为3。因为这种计算逻辑，该散列函数只会返回1到9的数字。

再回到散列表的样子。如果是用刚才的散列函数，那么该散列表的10到16号格子就都用不上了，数据只会被放到1到9的格子里。

所以，一个好的散列函数，应当能将数据分散到所有可用的格子里去。

如果一个散列表只需要保存5个值，那么它应该多大，以及采用什么散列函数呢？

要是散列表只有5个格子，那么散列函数需要算出1到 5的散列值。但就算我们想保存的值也只有5个，冲突还是很可能发生，因为散列值只有5种可能。

然而，如果散列表有100个格子，散列函数的结果为1到100之间的数，存5个值进去时发生冲突的可能性就小得多，因为落入的格子有100种可能。

尽管100个格子能很好地避免冲突，但只用来放5个值的话，就太浪费空间了。

这就是使用散列表时所需要权衡的：既要避免冲突，又要节约空间。

要想解决这个问题，可参考计算机科学家研究出的黄金法则：每增加7个元素，就增加10个格子。

如果要保存14个元素，那就得准备20个格子，以此类推。

数据量与格子数的比值称为负载因子。把这个术语代入刚才的理论，就是：理想的负载因子是0.7（7个元素/10个格子）。

如果你一开始就将7个元素放进散列表，那么计算机应该会创建出一个含有10个格子的散列表。随着你添加元素，计算机也会添加更多的格子来扩展这个散列表，并改变散列函数，使新数据能均匀地分布到新的格子里去。

幸运的是，一般编程语言都自带散列表的管理机制，它会帮你决定散列表的大小、散列函数的逻辑以及扩展的时机。既然你已经理解了散列表的原理，那么在处理一些问题时你就可以用它取代数组，利用其O(1)的查找速度来提升代码性能。

一个实例

散列表有各种用途，但目前我们只考虑用它来提高算法速度。

第1章我们学习了基于数组的集合--一种能保证元素不重复的数组。每次往其中插入新元素时，都要先做一次线性查找来确定该元素是否已存在（如果是无序数组）。

如果要在一个大集合上进行多次插入，效率将会下降得很快，因为每次插入都需要O(N)。

很多时候，我们都可以把散列表当成集合来用。

把数组作为集合的话，数据是直接放到格子里的。用散列表时，则是将数据作为键，值可以为任何形式，例如数字1，或者布尔值true也行。

假设在Javascript里建立了如下所示的散列表。

1	var set = {};

并加入一些数据。

1
2
3

set["apple"] = 1;
set["banana"] = 1;
set["cucumber"] = 1;

这样每次插入新值，都只需花O(1)的时间，而不是线性查找的O(N)。即使数据已存在时也是这个速度。

1	set["banana"] = 1;

再次插入”banana”时，我们并不需要检查它存在与否，因为即使存在，也只是将其对应的值重写成1。

散列表确实非常适用于检查数据的存在性。第4章我们讨论过如何在Javascript 里检查一个数组有没有重复数据。一开始的方案如下所示。

function hasDuplicateValue(array) 
{
    for(var i = 0; i < array.length; i++) 
    {
        for(var j = 0; j < array.length; j++) 
        {
            if(i !== j && array[i] == array[j]) 
            {
                return true;
            }
        }
    }
    return false;
}

当时我们说了，该嵌套循环的效率是O(N²)。

于是有了第二个O(N)的方案，不过它只能处理数据全为非负整数的数组。如果数组含有其他东西，例如字符串，那怎么办呢？

使用类似的逻辑，但换成散列表（在Javascript里叫作对象），就可以处理字符串了。

function hasDuplicateValue(array) 
{
    var existingValues = {};
    for(var i = 0; i < array.length; i++) 
    {
        if(existingValues[array[i]] === undefined) 
        {
            existingValues[array[i]] = 1;
        } 
        else 
        {
            return true;
        }
    }
    return false;
}

这种方法也是O(N)，其中的existingValues不是数组而是散列表，用字符串作为键（索引）是没有问题的。

假设我们要做一个电子投票机，投票者可以投给现有的候选人，也可以推荐新的候选人。因为会在选举的最后统计票数，我们可以将票保存在一个数组里，每投一票就将其插入到末尾。

var votes = [];
function addVote(candidate) 
{
    votes.push(candidate);
}

最终数组就会变得很长。

1	["Thomas Jefferson", "John Adams", "John Adams", "Thomas Jefferson", "John Adams", ...]

这样插入很快，只有O(1)。

那点票的效率又如何呢？因为票都在数组里，所以我们会用循环来遍历它们，并用一个散列表来记录每人的票数。

function countVotes(votes) 
{
    var tally = {};
    for(var i = 0; i < votes.length; i++) 
    {
        if(tally[votes[i]]) 
        {
            tally[votes[i]]++;
        } 
        else 
        {
            tally[votes[i]] = 1;
        }
    }
    return tally;
}

不过这样需要O(N)，也太慢了！

不如换种方式，一开始就用散列表来收集票数。

var votes = {};

function addVote(candidate) 
{
    if(votes[candidate]) 
    {
        votes[candidate]++;
    } 
    else 
    {
        votes[candidate] = 1;
    }
}

function countVotes() 
{
    return votes;
}

这样一来，投票是O(1)，并且因为投票时就已经在计数，所以已完成了点票的步骤。

总结

高效的软件离不开散列表，因为其O(1)的读取和插入带来了无与伦比的性能优势。

到现在为止，我们探讨各种数据结构时都只考虑了性能。但你知道有些数据结构的优点并不在于性能吗？下一章就研究两种能帮助改善代码可读性和可维护性的数据结构。