思考并回答以下问题:
- 什么是递归?递归适用于什么场景?
- 几乎所有循环都能够转换成递归怎么理解?
- 什么是基准情形?
- 如何阅读递归代码?
- 什么是调用栈?递归发生时内存是怎么处理的?
- 计算机处理3的阶乘的过程是什么样的?
- 什么是栈溢出,为什么会发生?
本章涵盖:
- 用递归代替循环
- 基准情形
- 阅读递归代码
- 计算机眼中的递归
- 递归实战
- 总结
在学习本书其余算法之前,你得先学会递归。解决很多看似复杂的问题时,如果从递归的角度去思考,会出人意料地简单,而且代码量还会大大减少。
不过,我们先做一个突击测试!
运行一个定义如下的blah()函数,会发生什么?1
2
3
4function blah()
{
blah();
}
正如你所想的,blah()会调用blah(),后者也会调用blah(),于是就这样无限地调用下去。
函数调用自身,就叫作递归。无限递归用处不大,甚至还挺危险,但是有限的递归很强大。掌控好递归能帮助我们解决某些棘手的问题,我很快就会证明给你看。
用递归代替循环
假设在NASA工作的你,需要写一个用于发射飞船的倒数程序。该程序接收一个数字,例如10,然后显示从10到0的数字。现在先暂停一下,选择一门编程语言来实现这个程序,做完以后,再往下阅读。
或许你用了JavaScript,并且写了如下循环。1
2
3
4
5
6
7
8function countdown(number)
{
for(var i = number; i >= 0; i--)
{
console.log(i);
}
}
countdown(10);
这样写没什么问题,只是你可能没想到循环以外的做法。
那还能怎么做呢?
试试换成递归吧。以下是初级版的递归countdown 。1
2
3
4
5
6function countdown(number)
{
console.log(number);
countdown(number - 1);
}
countdown(10)
让我们一步步来分析。
第1步:调用countdown(10),因此参数number为 10。
第2步:将number(值为10)打印到控制台。
第3步:countdown函数在结束前,调用了countdown(9)(因为number - 1等于 9)。
第4步:countdown(9)被执行,会将number(值为9)打印到控制台。
第5步:countdown(9)结束前,调用了countdown(8) 。
第6步:countdown(8)被执行,会将number(值为8)打印到控制台。
在继续步骤分解之前,先回顾下该递归是怎样实现我们的需求的。countdown里并没有任何循环结构,它通过调用自身就能够从10开始倒数并将每个数字打印出来。
几乎所有循环都能够转换成递归。但能用不代表该用。递归的强项在于巧妙地解决问题,但在上面的例子中,它并不比普通的循环更加优雅、高效。我们很快就会看到能让递归发挥威力的场景,但在那之前,还是先理清递归的运作方式。
基准情形
让我们把countdown函数继续下去。为了简洁一点,我们跳过一些步骤。
第21步:调用countdown(0) 。
第22步:将number(值为0)打印到控制台。
第23步:调用countdown(-1) 。
第24步:将number(值为1)打印到控制台。
糟了,你也看到了,这种写法不够完善,这样下去我们就会不断地打印负数。
要解决这个问题,得在数到0时就停住,以免递归一直往下数。
我们可以加个条件判断,来保证当number为0时,不再调用countdown()。1
2
3
4
5
6
7
8
9
10
11
12
13function countdown(number)
{
console.log(number);
if(number === 0)
{
return;
}
else
{
countdown(number - 1);
}
}
countdown(10);
这样,当number为0时,我们的代码就不会再去调用countdown(),而是直接返回。
在递归领域(真有这么一个地方),不再递归的情形称为基准情形。对于刚才的countdown()函数来说,0就是基准情形。
阅读递归代码
递归是需要时间和练习才能适应的,到那时候,你会掌握两种技巧:阅读递归代码和编写递归代码。阅读递归代码相对简单一点,所以就先从这里入手吧。
我们会以阶乘作为例子。阶乘的演示如下所示。
3的阶乘是:
3 2 1 = 6
5的阶乘是:
5 4 3 2 1 = 120
以此类推。以下Ruby代码会以递归计算的方式返回一个数的阶乘。1
2
3
4
5
6
7def factorial(number)
if number == 1
return 1
else
return number * factorial(number - 1)
end
end
此代码初看可能会让人有点困惑,可以按照以下流程来读。
(1) 找出基准情形。
(2) 看该函数在基准情形下会做什么。
(3) 看该函数在到达基准情形的前一步会做什么。
(4) 就这样往前推,看每一步都在做什么。
让我们将此流程应用到刚才的代码上。稍作分析,就可以看出里面有两条路径。1
2
3
4
5if number == 1
return 1
else
return number * factorial(number - 1)
end
第二条路的factorial有调用自身,是递归发生的地方。1
2
3else
return number * factorial(number - 1)
end
第一条路并没有调用自身,因此这里是基准情形。1
2if number == 1
return 1
于是,number为1时,是基准情形。
接着,想象factorial方法在基准情形下,即factorial(1) 的处理流程。其相关代码如下。1
2if number == 1
return 1
好,这很简单,因为是基准情形,所以没有递归。调用factorial(1)就会直接返回1。于是找来一张纸,记下该结果。
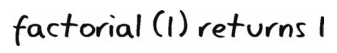
然后,回到上一步的factorial(2),相关代码如下。1
2
3else
return number * factorial(number - 1)
end
调用factorial(2)就会返回2 factorial(1) 。要计算2 factorial(1),就得先知道factorial(1)的结果。要是检查下前面所记,你会发现那是1。因此,2 factorial(1)就是2 1 ,即是2。
把这个也记到纸上。
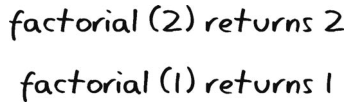
那么,factorial(3)又会是什么呢?再回看代码。1
2
3else
return number * factorial(number - 1)
end
代入参数便是3 factorial(2) 。那么factorial(2)是什么呢?你不用从头计算,因为它的结果已经写在纸上了,是2。于是factorial(3)会返回 6(3 2 = 6)。将结果记下,然后继续。

现在请自行计算factorial(4) 。
如你所见,这种从基准情形入手再往上分析的思路,对理解递归代码是多么有益。
事实上,此方法不仅为人类所利用,计算机也差不多是这样做的。下面就来看看。
计算机眼中的递归
细想一下我们的factorial方法,你会发觉当factorial(3)执行时,会有如下事情发生。
计算机调用factorial(3),并在该方法返回前,调用了factorial(2),而在factorial(2)返回前,又调用了factorial(1)。从技术上来说,当计算机执行factorial(1)时,它其实还在factorial(2)之中,而factorial(2)又正在factorial(3)之中。
计算机是用栈来记录每个调用中的函数。这个栈就叫作调用栈。
让我们以factorial为例来观察调用栈如何运作。
起初计算机调用的是factorial(3)。然而,在该方法完成之前,它又调用了factorial(2)。为了记住自己还在factorial(3)中,计算机将此事压入调用栈中。
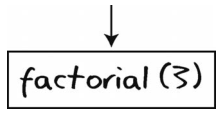
接着计算机开始处理factorial(2)。该factorial(2)会调用factorial(1)。不过在进入factorial(1)前,计算机得记住自己还在factorial(2)中,于是,它将此事也压入调用栈中。
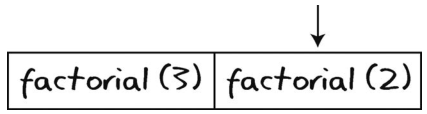
然后计算机执行factorial(1)。因为1已经是基准情形了,所以它可以返回,不用再调用factorial。
尽管factorial(1)结束了,但调用栈内仍存在数据,意味着整件事还没完,计算机还处于其他函数当中。你应该还记得,栈的规定是只有栈顶元素(即最后的元素)才能被看到。所以,计算机接下来就去检查了调用栈的栈顶,发现那是factorial(2)。
由于factorial(2)是调用栈的最后一项,因此代表最近调用并且最应该先完成的是factorial(2)。
于是计算机将factorial(2)从调用栈弹出。
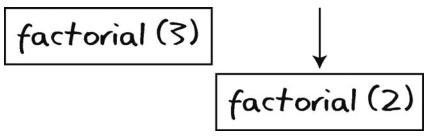
并将其结束。
然后计算机再次检查调用栈,看下一步应该结束哪个方法。调用栈如下所示。

于是计算机将factorial(3)从调用栈弹出,并将其结束。
到这里,调用栈就清空了,计算机也因此得知所有方法都执行完了,递归结束。
从更高的角度去看,可以看出计算机处理3的阶乘时,步骤如下。
(1)factorial(3)被第一个调用。
(2)factorial(2)被第二个调用。
(3)factorial(1)被第三个调用。
(4)factorial(1)被第一个完成。
(5)factorial(2)在factorial(1)的基础上完成。
(6)最后,factorial(3)在factorial(2)的基础上完成。
有趣的是,无限递归(如本章开头的例子)的程序会一直将同一方法加到调用栈上,直到计算机的内存空间不足,最终导致栈溢出的错误。
递归实战
虽然上面的NASA倒数程序和阶乘计算能用递归来解决,但用普通的循环来做也不难。除了好玩以外,递归在这些问题上没体现出什么优势。
事实上,递归可以自然地用于实现那些需要重复自身的算法。在这些情况下,递归可以增强代码的可读性,你接下来就会看到。
比如说遍历文件系统。假设你现在要写一个脚本,它用于对一个目录下的所有文件进行某种操作。这里的“所有文件”,不仅指的是该目录中的文件,还包括其子目录的文件,以及子目录里的子目录的文件,以此类推。
我们先用Ruby写一个打印某目录下所有子目录名字的脚本。1
2
3
4
5
6
7
8
9def find_directories(directory)
Dir.foreach(directory) do |filename|
if File.directory?("#{directory}/#{filename}") && filename != "." && filename != ".."
puts "#{directory}/#{filename}"
end
end
end
# 以当前目录为参数,调用 find_directories
find_directories(".")
此脚本遍历给定目录下的所有文件。当遇到的某个文件为子目录时(即文件类型为目录,但又不是代表“当前目录”“上级目录”的句号和双句号的那些文件),将其名字打印出来。
虽然这跑起来没问题,但它只打印了当前目录的直属子目录的名字,并没有打印出那些子目录的子目录的名字。
接着我们改进一下,使该脚本能再深入到下一层目录。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17def find_directories(directory)
# 遍历给定目录下的文件
Dir.foreach(directory) do |filename|
if File.directory?("#{directory}/#{filename}") &&
filename != "." && filename != ".."
puts "#{directory}/#{filename}"
# 遍历其子目录下的文件
Dir.foreach("#{directory}/#{filename}") do |inner_filename|
if File.directory?("#{directory}/#{filename}/#{inner_filename}") &&inner_filename != "." && inner_filename != ".."
puts "#{directory}/#{filename}/#{inner_filename}"
end
end
end
end
end
# 以当前目录为参数,调用 find_directories
find_directories(".")
这样,我们就可以对每个子目录再发起另一个循环去遍历其中的孙子目录了。不过,它只能进到两层目录的深度而已。如果我们还想进到第三层、第四层、第五层,甚至最底层,那要怎么做呢?以目前的思路似乎不可能实现。
这就是递归出马的时候了。使用递归的话,我们可以写一个进入任意深度的脚本,而且很简洁!1
2
3
4
5
6
7
8
9
10
11def find_directories(directory)
Dir.foreach(directory) do |filename|
if File.directory?("#{directory}/#{filename}") &&
filename != "." && filename != ".."
puts "#{directory}/#{filename}"
find_directories("#{directory}/#{filename}")
end
end
end
# 以当前目录为参数,调用 find_directories
find_directories(".")
find_directories会对所遇到的每个子目录再调用find_directories 。这样一来,所有子目录都会被挖出来,没有一个会漏掉。
此算法如下图所示,其中的号码代表目录被访问的顺序。
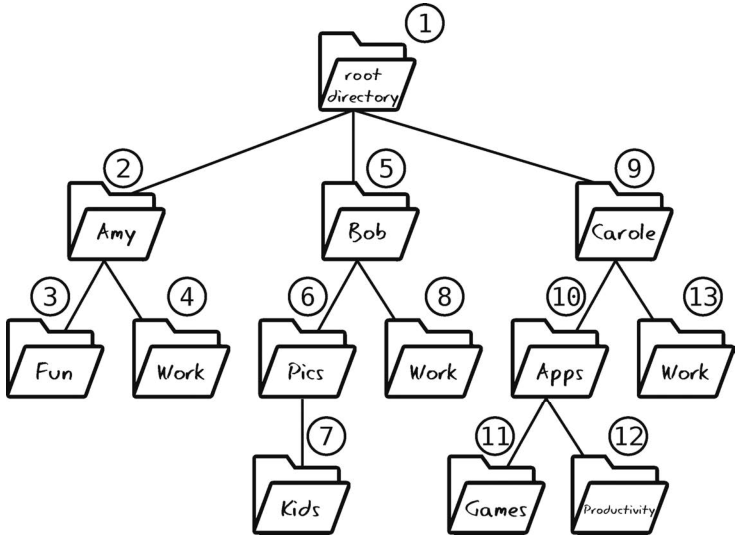
注意,改用递归并不会改变算法的大O。但是,在下一章你会看到,递归可以作为算法的核心组件,影响算法的速度。
总结
正如文件系统的例子所示,递归十分适用于那些无法预估计算深度的问题。
掌握递归,你就解锁了一批高效但更为高深的算法。它们都离不开递归的原理。
C#遍历指定文件夹下的所有文件和所有子目录