第11章-基于结点的数据结构

思考并回答以下问题：

• 数组和链表有什么区别？
• 什么是链表？什么是结点？什么是链？每个结点需要几个格子？
• 链表的第一个节点有什么作用？
• 链表的物理结构与数组不同怎么理解？链表相对数组有什么好处？
• 用一种语言来实现链表。写链表需要两个类，哪两个？为什么？
• 链表的读取和查找如何进行？是什么时间复杂度？
• 链表的开头插入和末尾插入如何进行？是什么时间复杂度？
• 什么场景适合使用链表？链表在删除操作中有优势，也是可实际使用的地方。怎么理解？
• 链表的另一个引人注目的应用，就是作为队列的底层数据结构。为什么？
• 什么是双向链表？

本章涵盖：

• 链表
• 实现一个链表
• 读取
• 查找
• 插入
• 删除
• 链表实战
• 双向链表

接下来的几章将要学习的各种数据结构，都涉及一种概念--结点。基于结点的数据结构拥有独特的存取方式，因此在某些时候具有性能上的优势。

本章我们会探讨链表，它是最简单的一种基于结点的数据结构，而且也是后续内容的基础。

你会发现，虽然链表和数组看上去差不多，但在性能上却各有所长。

链表

像数组一样，链表也用来表示一系列的元素。事实上，能用数组来做的事情，一般也可以用链表来做。然而，链表的实现跟数组是不一样的，在不同场景它们会有不同的性能表现。

计算机的内存就像一大堆格子，每格都可以用来保存比特形式的数据。当要创建数组时，程序会在内存中找出一组连续的空格子，给它们起个名字，以便你的应用存放数据，见下图。

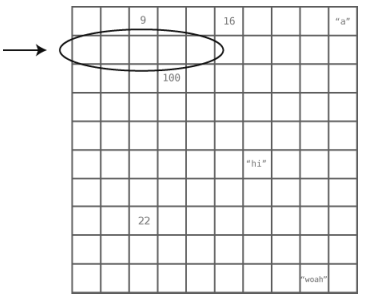
我们之前说过，计算机能够直接跳到数组的某一索引上。如果代码要求它读取索引4的值，那么计算机只需一步就可以完成任务。重申一次，之所以能够这样，是因为程序事先知道了数组开头所在的内存地址--例如地址是1000--当它想去索引4时，便会自动跳到1004处。

与数组不同的是，组成链表的格子不是连续的。它们可以分布在内存的各个地方。这种不相邻的格子，就叫作结点。

那么问题来了，计算机怎么知道这些分散的结点里，哪些属于这个链表，哪些属于其他链表呢？

这就是链表的关键了：每个结点除了保存数据，它还保存着链表里的下一结点的内存地址。

这份用来指示下一结点的内存地址的额外数据，被称为链。链表如下图所示。

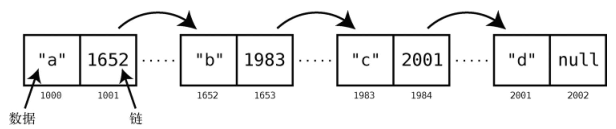
此例中，我们的链表包含4项数据：“a”、“b”、“c”和“d”。因为每个结点都需要2个格子，头一格用作数据存储，后一格用作指向下一结点的链（最后一个结点的链是null，因为它是终点），所以整体占用了8个格子。

若想使用链表，你只需知道第一个结点在内存的什么位置。因为每个结点都有指向下一结点的链，所以只要有给定的第一个结点，就可以用结点1的链找到结点2，再用结点2的链找到结点3……如此遍历链表的剩余部分。

链表相对于数组的一个好处就是，它可以将数据分散到内存各处，无须事先寻找连续的空格子。

实现一个链表

我们用Ruby来写一个链表，最终实现包含两个类：Node和LinkedList 。先是Node。

class Node
    # 创建读写变量data,next_node
    attr_accessor :data, :next_node 

    def initialize(data)
        @data = data
    end
end

Node类有两个属性：data表示结点所保存的数据，next_node表示指向下一结点的链，使用方法如下。

node_1 = Node.new("once")
node_2 = Node.new("upon")
node_1.next_node = node_2
node_3 = Node.new("a")
node_2.next_node = node_3
node_4 = Node.new("time")
node_3.next_node = node_4

以上代码创建了4个连起来的结点，它们分别保存着“once”、“upon”、“a”和“time”4项数据。

虽然只用Node也可以创建出链表，但我们的程序无法由此轻易地得知哪个结点是链表的开端。因此我们还得创建一个LinkedList类。下面是一个最基本的LinkedList的写法。

class LinkedList

    attr_accessor :first_node

    def initialize(first_node)
        @first_node = first_node
    end
end

有了这个类，我们就可以用以下代码让程序知道链表的起始位置了。

list = LinkedList.new(node_1)

LinkedList的作用就是一个指针，它指向链表的第一个结点。

既然知道了链表是什么，那么接下来做个它跟数组的性能对比，观察它们在读取、查找、插入和删除上有何优劣。

读取

我们曾经说过，当计算机要从数组中读取一个值时，它会一步跳到对应的格子上，其效率为O(1)。但在链表中就不是这样了。

假设程序要读取链表中索引2的值，计算机不可能在一步之内完成，因为无法一下子算出它在内存的哪个位置。毕竟，链表的结点可以分布在内存的任何地方。程序知道的只有第1个结点的内存地址，要找到索引2的结点（即第3个），程序必须先读取索引0的链，然后顺着该链去找索引1。接着再读取索引1的链，去找索引2，这才能读取到索引2里的值。

下面我们在LinkedList类中加入读取操作。

class LinkedList
    
    attr_accessor :first_node

    def initialize(first_node)
        @first_node = first_node
    end

    def read(index)
        # 从第一个结点开始
        current_node = first_node
        current_index = 0

        while current_index < index do
            # 顺着链往下找，直至我们要找的那个索引值
            current_node = current_node.next_node
            current_index += 1

            # 如果读到最后一个结点之后，就说明
            # 所找的索引不在链表中，因此返回 nil
            return nil unless current_node
        end
        return current_node.data
    end
end

当想要读取某个索引时，可以这样写：

list.read(3)

读取链表中某个索引值的最坏情况，应该是读取最后一个索引。这种情况下，因为计算机得从第一个结点开始，沿着链一直读到最后一个结点，于是需要N步。由于大O记法默认采用最坏情况，所以我们说读取链表的时间复杂度为O(N)。这跟读取数组的O(1)相比，的确是一大劣势。

查找

链表的查找效率跟数组一样。记住，所谓查找就是从列表中找出某个特定值所在的索引。对于数组和链表来说，它们都是从第一格开始逐个格子地找，直至找到。如果是最坏情况，即所找的值在列表末尾，或完全不在列表里，那就要花O(N)步。

下面是查找方法的实现。

class LinkedList
    
    attr_accessor :first_node
    # 其他方法略……

    def index_of(value)
        # 从第一个结点开始
        current_node = first_node
        current_index = 0

        begin
            # 如果找到，就返回
            if current_node.data == value
                return current_index
            end

            # 否则，看下一个结点
            current_node = current_node.next_node
            current_index += 1
        end while current_node

        # 如果遍历整个链表都没找到，就返回 nil
        return nil
    end
end

有了它我们就可以这样来查找了：

list.index_of("time")

插入

在某些情况下，链表的插入跟数组相比，有着明显的优势。回想插入数组的最坏情况：当插入位置为索引0时，因为需要先将插入位置右侧的数据都右移一格，所以会导致O(N)的时间复杂度。然而，若是往链表的表头进行插入，则只需一步，即O(1)。下面看看为什么。

假设我们的链表如下所示。

要在表头增加“yellow”，我们只需创建一个新的结点，然后使其链接到“blue”那一结点。

因为无须平移其他数据，所以与数组相比，链表在前端插入数据更为便捷。

虽然理论上在链表的任何一处做插入都只需要1步，但事实上没那么简单。假设现在链表是这样的：

然后我们想在索引2（“blue”和“green”之间）插入“purple”。由于插入动作创建了一个新的结点，如下图那样改动“blue”和“purple”的链，因此实际的操作只需1步。

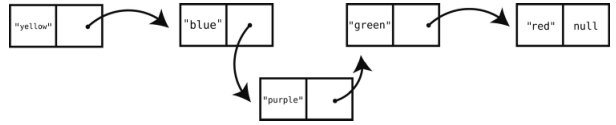
但是，在该动作之前，计算机还得先找到索引1的结点（“blue”），让结点1的链指向新的结点。这个过程就是之前所说的读取链表，其效率为O(N)。下面我们来演示一下。

因为新结点是加在索引1之后，所以计算机要先找出索引1。这得从第一个结点开始。

接着通过第一个链访问下一个结点。

既然已到达索引1的结点，那就可以增加新的结点进去了。

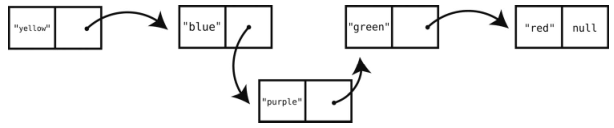
刚才添加“purple”的例子花了3步。若想将它添加到链表的末尾，就得花5步：先是用4步跳到索引3上，再用1步插入新结点。

因此，链表的插入效率为O(N)，与数组一样。

有趣的是，通过以上分析，你会发现链表的最坏情况和最好情况与数组刚好相反。在链表开头插入很方便，在数组开头插入却很麻烦；在数组的末尾插入是最好情况，在链表的末尾插入却是最坏情况。总结起来如下表所示。

场 景	数 组	链 表
在前端插入	最坏情况	最好情况
在中间插入	平均情况	平均情况
在末端插入	最好情况	最坏情况

下面给LinkedList类加上插入方法。

class LinkedList
attr_accessor :first_node
    # 其他方法略……

    def insert_at_index(index, value)
        # 创建新结点
        new_node = Node.new(value)
        # 如果在开头插入，则将新结点的 next_node 指向原 first_node，
        # 并为其设置新的 first_node
        if index == 0
            new_node.next_node = first_node
            return @first_node = new_node
        end

        current_node = first_node
        current_index = 0
        # 先找出新结点插入位置前的那一结点
        prev_index = index - 1
        while current_index < prev_index do
            current_node = current_node.next_node
            current_index += 1
        end
        
        new_node.next_node = current_node.next_node
        # 使前一结点的链指向新结点
        current_node.next_node = new_node
    end
end

删除

从效率上来看，删除跟插入是相似的。如果删除的是链表的第一个结点，那就只要1步：将链表的first_node设置成当前的第二个结点。

回到“once”、“upon”、“a”和“time”的例子。如果要删除“once”，那直接让链表以“upon”为开头就好了。

list.first_node = node_2

再回想删除数组的第一个元素时，得把剩余的所有元素左移一格，需要O(N)的时间复杂度。

删除链表的最后一个结点，其实际的删除动作只需1步--令倒数第二的结点的链指向null。

然而，要找出倒数第二的结点，得花N步，因为我们依然只能从第一个结点顺着链往下一个个地找。

下面这个表格对比了各种情况下数组和链表删除操作的效率。注意它跟插入效率的表格几乎一模一样。

场 景	数 组	链 表
在前端删除	最坏情况	最好情况
在中间删除	平均情况	平均情况
在末端删除	最好情况	最坏情况

要在链表中间做删除，计算机需要修改被删结点的前一结点的链，看下面的例子你就会明白。

假设现在要删除刚才例子的索引2的值（“purple”），计算机就会找出索引1的结点，将其链指向”green”结点。

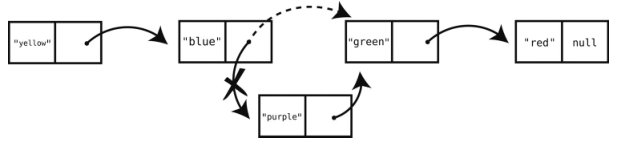
LinkedList类的删除操作实现如下。

class LinkedList attr_accessor :first_node
    # 其他方法略……

    def delete_at_index(index)
        # 如果删除的是第一个结点，
        # 则将 first_node 重置为第二个结点，
        # 并返回原第一个结点
        if index == 0
            deleted_node = first_node
            @first_node = first_node.next_node
            return deleted_node
        end

        current_node = first_node
        current_index = 0
        # 先找出被删结点前的那一结点，
        # 将其命名为 current_node
        while current_index < index - 1 do
            current_node = current_node.next_node
            current_index += 1
        end

        # 再找出被删结点后的那一结点
        deleted_node = current_node.next_node
        node_after_deleted_node = deleted_node.next_node
        # 将 current_node 的链指向 node_after_deleted_node，
        # 这样被删结点就被排除在链表之外了
        current_node.next_node = node_after_deleted_node
        deleted_node
    end
end

经过一番分析，链表与数组的性能对比如下所示。

操 作	数 组	链 表
读取	O(1)	O(N)
查找	O(N)	O(N)
插入	O(N)（在末端是O(1)）	O(N)（在前端是O(1)）
删除	O(N)（在末端是 O(1)）	O(N)（在前端是O(1)）

尽管两者的查找、插入、删除的效率看起来差不多，但在读取方面，数组比链表要快得多。

既然如此，那为什么还要用链表呢？

链表实战

高效地遍历单个列表并删除其中多个元素，是链表的亮点之一。假设我们正在写一个整理电子邮件地址的应用，它会删掉列表中无效格式的地址。具体算法是，每次读取一个地址，然后用正则表达式（一种用于识别数据格式的特定模式）来校验其有效性。如果发现该地址无效，就将它从列表中移除。

不管这个列表是数组还是链表，要检查每个元素的话，都得花N步。然而，当要删除邮件地址时，它们的效率却不同，下面我们来验证一下。

用数组的话，每次删除邮件地址，我们就要另外再花O(N)步去左移后面的数据，以填补删除所产生的空隙。而且还必须完成这些平移才能执行下一次邮件地址的检查。

所以如果存在需要删除的无效地址，那么除了遍历邮件地址的N步，还得加上N步乘以无效地址数。

假设每10个地址就有1个是无效的。如果列表包含1000个地址，那么无效的就应该会有100个。于是我们的算法就要花1000步来读取，再加上删除所带来的大约100000步的操作（100个无效地址 × N）。

但要是链表的话，每次删除只需1步就好，因为只需改动结点中链的指向，然后就可以继续检查下一邮件地址了。按这种算法去处理1000个邮件地址，只需要1100步（1000步读取和100步删除）。

双向链表

链表的另一个引人注目的应用，就是作为队列的底层数据结构。第8章我们已经介绍过队列，你应该还记得它就是一种只能在末尾插入元素，在开头删除元素的数据结构。当时我们用数组作为队列的底层，并解释说队列只是有约束条件的数组。其实，改用链表来做队列的底层也可以，同样地，只要使该链表的元素只在末尾插入，并在开头删除就好了。那么用链表来代替数组有什么好处呢？下面来分析一下。

再强调一次，队列插入数据只能在末尾。如上文所述，在数组的末尾插入是极快的，时间复杂度为O(1)。链表则要O(N)。所以在插入方面，选择数组比链表更好。

但到了删除的话，就是链表更快了，因为它只要O(1)，而数组是O(N)。

基于以上分析，似乎用数组还是链表都无所谓。因为它们总有一种操作是O(1)，另一种是O(N)：数组的插入是O(1)，删除是O(N)；链表则反过来，分别是O(N)和O(1)。

然而，要是采用双向链表这一链表的变种，就能使队列的插入和删除都为O(1)。

双向链表跟链表差不多，只是它每个结点都含有两个链--一个指向下一结点，另一个指向前一结点。此外，它还能直接访问第一个和最后一个结点。

以下是一个双向链表。

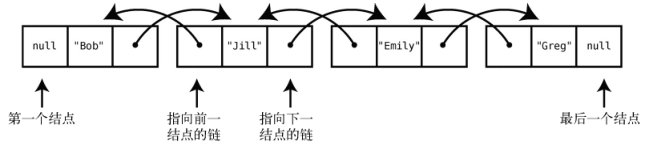
用代码来表述的话，如下所示。

class Node

    attr_accessor :data, :next_node, :previous_node

    def initialize(data)
        @data = data
    end
end

class DoublyLinkedList
    
    attr_accessor :first_node, :last_node

    def initialize(first_node=nil, last_node=nil)
        @first_node = first_node
        @last_node = last_node
    end
end

由于双向链表总会记住第一个和最后一个结点，因此能够一步（以O(1)的时间）访问到它们。

更进一步地，在末尾插入数据也可以一步完成，如下所示。

这里创建了一个新结点（“Sue”），并使其previous_node指向双向链表的last_node(“Greg”)。然后，再将last_node(“Greg”)的next_node指向这个新结点（“Sue”）。最后，把last_node改为新结点（“Sue”）。

以下是在双向链表中实现的新方法insert_at_end 。

class DoublyLinkedList
    
    attr_accessor :first_node, :last_node
    
    def initialize(first_node=nil, last_node=nil)
        @first_node = first_node
        @last_node = last_node
    end

    def insert_at_end(value)
        new_node = Node.new(value)
        # 如果链表还没有任何结点
        if !first_node
            @first_node = new_node
            @last_node = new_node

        else
            new_node.previous_node = @last_node
            @last_node.next_node = new_node
            @last_node = new_node
        end
    end
end

因为双向链表能直接访问前端和末端的结点，所以在两端插入的效率都为O(1)，在两端删除的效率也为O(1)。由于在末尾插入和在开头删除都能在O(1)的时间内完成，因此拿双向链表作为队列的底层数据结构就最好不过了。

以下是基于双向链表的队列的完整代码示例。

class Node
    attr_accessor :data, :next_node, :previous_node
    
    def initialize(data)
        @data = data
    end
end

class DoublyLinkedList
    
    attr_accessor :first_node, :last_node
    
    def initialize(first_node=nil, last_node=nil)
        @first_node = first_node
        @last_node = last_node
    end

    def insert_at_end(value)
        new_node = Node.new(value)
        # 如果链表还没有任何结点
        if !first_node
            @first_node = new_node
            @last_node = new_node
        else
            new_node.previous_node = @last_node
            @last_node.next_node = new_node
            @last_node = new_node
        end
    end

    def remove_from_front
        removed_node = @first_node
        @first_node = @first_node.next_node
        return removed_node
    end
end

class Queue
    
    attr_accessor :queue
    
    def initialize
        @queue = DoublyLinkedList.new
    end
    
    def enque(value)
        @queue.insert_at_end(value)
    end
   
    def deque
        removed_node = @queue.remove_from_front
        return removed_node.data
    end

    def tail
        return @queue.last_node.data
    end
end

总结

尽管目前还没用到队列，或者用了数组但没用双向链表也运行得很好。但是现在，你知道了还有其他选择，也学习了什么时候应该做出什么选择。

你学会了在特定情况下使用链表来改善性能。后面还会介绍更复杂的基于结点的数据结构，它们更常用，并且对性能的提升更大。