思考并回答以下问题:
- 什么是树?什么是二叉树?
- 二叉树既可以保持顺序,又可以快速查找、插入和删除。为什么?
- 先创建节点类,然后再用节点对象构建二叉树类。怎么理解?
- 二叉树查找的时间复杂度是O(log N)。因为每行进一步,我们就把剩余的结点排除了一半。怎么理解?
本章涵盖:
- 二叉树
- 查找
- 插入
- 删除
- 二叉树实战
之前介绍了二分查找这一概念,并演示了当数组有序时,运用二分查找就能以O(log N)的时间复杂度找出任意值的所在位置。可见,有序的数组是多么美好。
但是有序数组存在着另一个问题。
有序数组的插入和删除是缓慢的。往有序数组中插入一个值前,你得将所有大于它的元素右移一格。从有序数组中删除一个值后,你得将所有大于它的元素左移一格。最坏情况下(插入或删除发生在数组开头)这会需要N步,平均情况则是N/2步。不管怎样,都是O(N)的效率,而O(N)算是挺慢的。
后来,学到了散列表能以O(1)的效率进行查找、插入和删除,但它又有另一明显的不足:不保持顺序。
既要保持顺序,又要快速查找、插入和删除,看来有序数组和散列表都不行。那还有什么数据结构可以选择?
看看二叉树吧。
二叉树
上一章我们通过链表见识了基于结点的数据结构。一个普通的链表里,每一个结点会包含一个连接自身和另一结点的链。树也是基于结点的数据结构,但树里面的每个结点,可以含有多个链分别指向其他多个结点。
以下是一棵典型的树
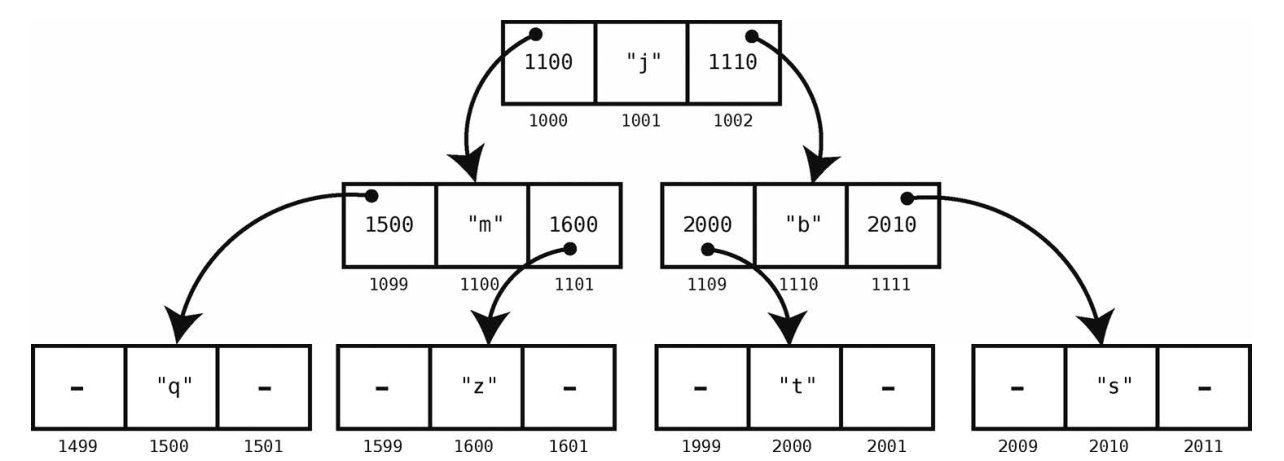
此例中,每个结点链接着另外两个结点。简单起见,我们也可以不用画出存储链的格子。
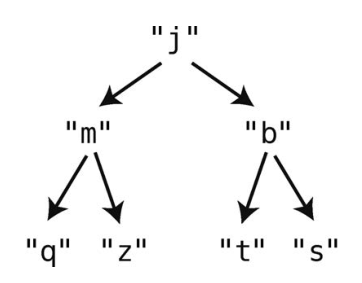
谈论树的时候,我们会用到以下术语。
- 最上面的那一结点(此例中的“j”)被称为根。是的,图中的根位于树的顶端,请自行意会。
- 此例中,“j”是“m”和“b”的父结点,反过来,“m”和“b”是“j”的子结点。“m”又是“q”和“z”的父结点,“q”和“z”是“m”的子结点。
- 树可以分层。此例中的树有3层。
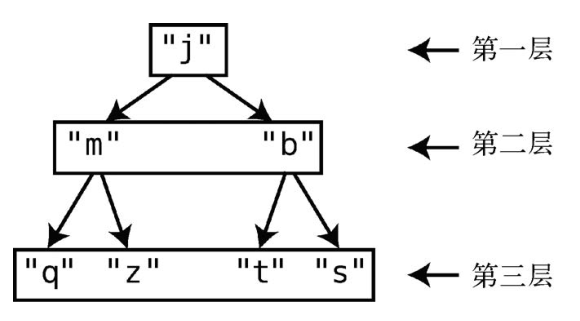
基于树的数据结构有很多种,但本章只关注其中一种--二叉树。二叉树是一种遵守以下规则的树。
- 每个结点的子结点数量可为0、1、2。
- 如果有两个子结点,则其中一个子结点的值必须小于父结点,另一个子结点的值必须大于父结点。
以下是一个二叉树的例子,其中结点的值是数字。
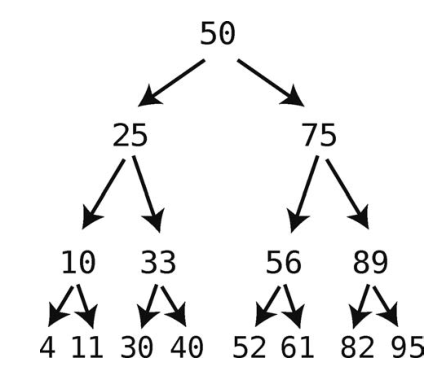
注意,小于父结点的子结点用左箭头来表示,大于父结点的子结点则用右箭头来表示。
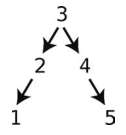
尽管下图是一棵树,但它不是二叉树。
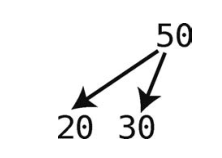
之所以不是二叉树,是因为它的两个子结点的值都小于父结点。
以Python来实现一个树结点的话,大概是这样:1
2
3
4
5class TreeNode:
def __init__(self,val,left=None,right=None):
self.value = val
self.leftChild = left
self.rightChild = right
然后就可以用它来构建一棵简单的树了。1
2
3node = TreeNode(1)
node2 = TreeNode(10)
root = TreeNode(5, node, node2)
因为二叉树具有这样独特的结构,所以我们能在其中非常快速地进行查找操作,下面就来看看。
查找
这是一棵二叉树。
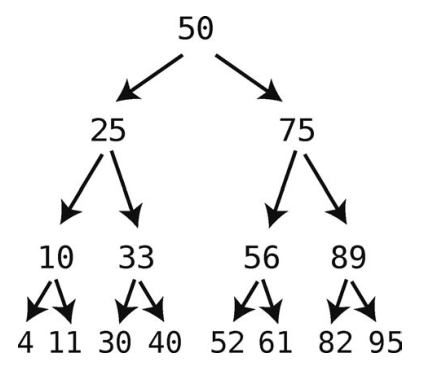
二叉树的查找算法先从根结点开始。
- (1)检视该结点的值。
- (2)如果正是所要找的值,太好了!
- (3)如果要找的值小于当前结点的值,则在该结点的左子树查找。
- (4)如果要找的值大于当前结点的值,则在该结点的右子树查找。
以下是用Python写的递归式查找。1
2
3
4
5
6
7
8
9
10
11
12
13def search(value, node):
# 基准情形:如果 node 不存在
# 或者 node 的值符合
if node is None or node.value == value:
return node
# 如果 value 小于当前结点,那就从左子结点处查找
elif value < node.value:
return search(value, node.leftChild)
# 如果 value 大于当前结点,那就从右子结点处查找
else: # value > node.value
return search(value, node.rightChild)
假设现在我们要找61,那来看看整个过程要花多少步。
树的查找必须从根开始。
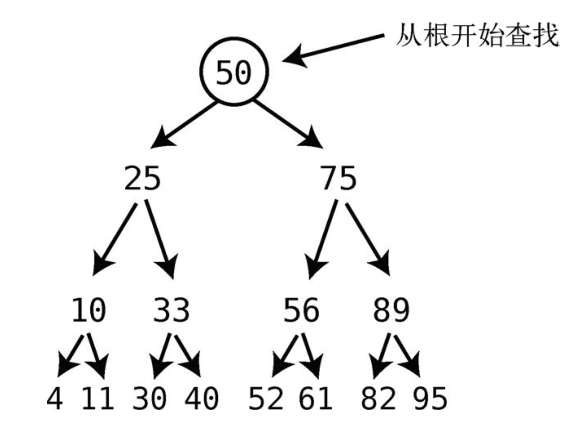
接着,计算机会问自己:我们要找的值与该结点的值相比,是大还是小呢?如果小于当前结点,那就在左子结点上找。如果大于当前结点,那就在右子结点上找。
本例中,因为61大于50,所以它只能在树的右侧,于是我们检查右子结点。
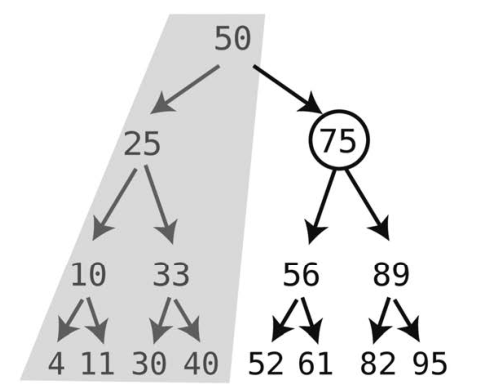
算法继续检查该结点的值。因为75不是我们要找的61,所以还得往下一层找。由于61小于75,它只能在75的左侧,于是下一步去的是左子结点。
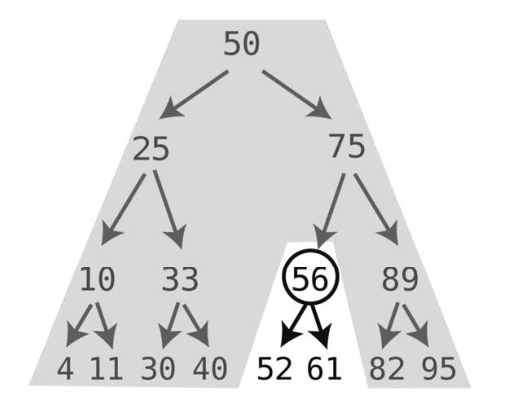
因为 61大于 56,所以到 56的右子结点上找。
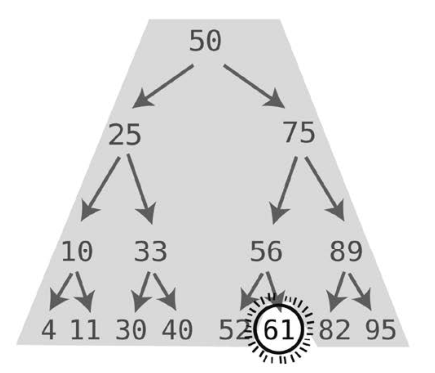
在这棵树里找出61,我们总共用了4步。
推广开来,我们会说二叉树查找的时间复杂度是O(log N)。因为每行进一步,我们就把剩余的结点排除了一半(不过很快就能看到,只在最好情况下,即理想的平衡二叉树才有这样的效率)。
再与二分查找比较,它也是每次尝试会排除一半可能性的O(log N)算法,可见二叉树查找跟有序数组的二分查找拥有同样的效率。
要说二叉树哪里比有序数组更亮眼,那应该是插入操作。
插入
要探索二叉树插入的算法,我们还是从一个实例入手吧。假设现在要往刚才的树里插入45。
首先要做的就是找出45应该被链接到哪个结点上。先从根开始找起。
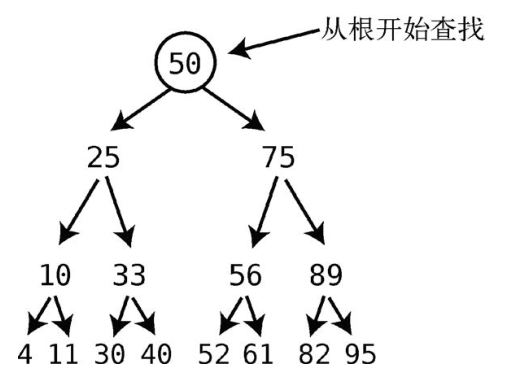
因为45小于50,所以我们转到左子结点上。
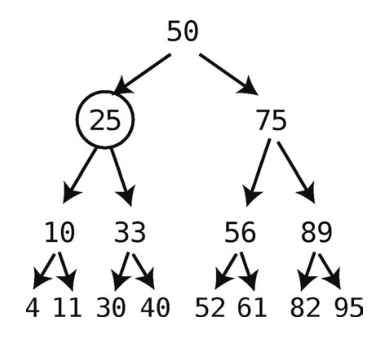
因为45大于25,所以我们检查右子结点。
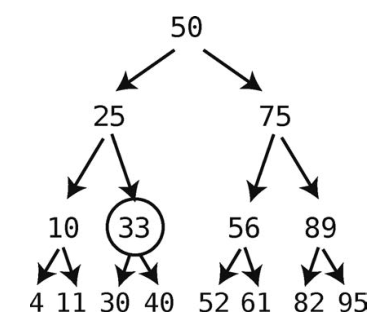
45大于33,所以检查33的右子结点。
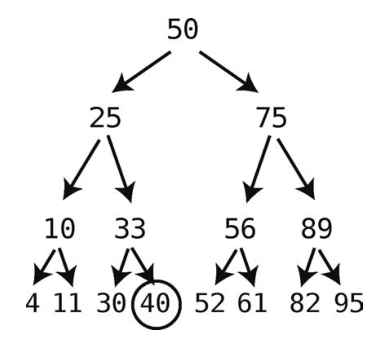
至此,我们到达了一个没有子结点的结点,也就无法再往下了。这意味着可以做插入了。
因为45大于40,所以将其作为40的右子结点来插入。
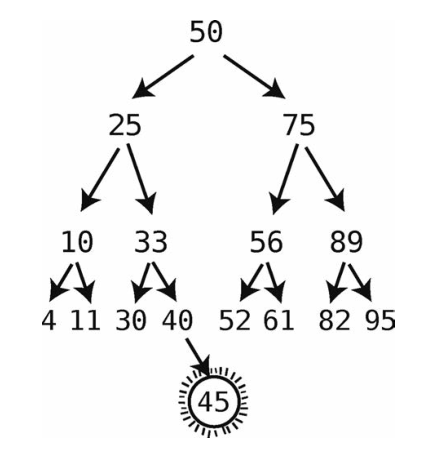
在这个例子里,插入花了5步,包括4步查找和1步插入。插入这1步总是发生在查找之后,所以总共log N+1步。按照忽略常数的大O来说,就是O(log N)步。
有序数组的插入则是O(N),因为该过程中除了查找,还得移动大量的元素来给新元素腾出空间。
这就是二叉树的高效之处。有序数组查找需要O(log N),插入需要O(N),而二叉树都是只要O(log N)。当你估计应用会发生许多数据改动时,这一比较将有助你做出正确选择。
以下是二叉树插入的Python实现,它跟search一样都是递归的。1
2
3
4
5
6
7
8
9
10
11
12
13def insert(value, node):
if value < node.value:
# 如果左子结点不存在,则将新值作为左子结点
if node.leftChild is None:
node.leftChild = TreeNode(value)
else:
insert(value, node.leftChild)
elif value > node.value:
# 如果右子结点不存在,则将新值作为右子结点
if node.rightChild is None:
node.rightChild = TreeNode(value)
else:
insert(value, node.rightChild)
注意,只有用随意打乱的数据创建出来的树才有可能是比较平衡的。要是插入的都是已排序的数据,那么这棵树就失衡了,它用起来也会比较低效。比如说,按顺序插入1、2、3、4、5的话,得出的树就会是这样。
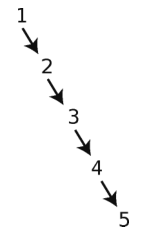
从中查找5,效率会是O(N)。
但要是按3、2、4、1、5的顺序来插入的话,得出的树就是平衡的。
因此,假若你要用有序数组里的数据来创建二叉树,最好先把数据洗乱。
在完全失衡的最坏情况下,二叉树的查找需要O(N)。在理想平衡的最好情况下,则是O(log N)。在数据随机插入的一般情况下,因为树也大致平衡,所以查询效率也大约是O(log N)。
删除
删除是二叉树的各种操作中最麻烦的一个,必须考虑周全才好动手。假设现在要删除这棵二叉树中的4。
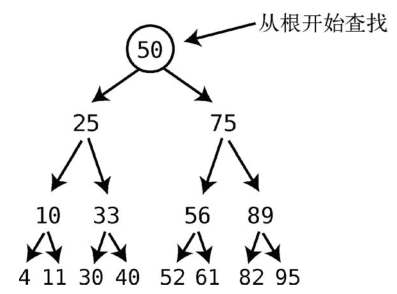
首先,我们查找出它所在的结点,然后一步将该结点删掉。
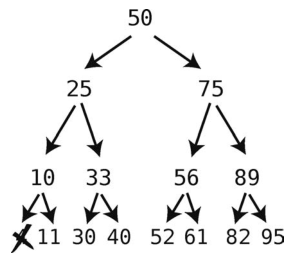
这看起来好像很简单,那我们再试试删掉10吧。
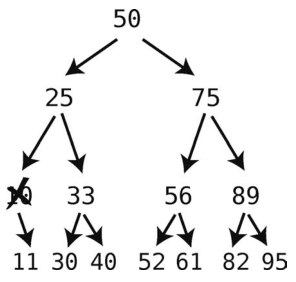
如果删掉10的话,就会导致11的那个结点从树上脱离。当然这是不允许的,否则这个11就永远都找不到了。好在我们还有解决办法:将11放到之前10所在的位置。
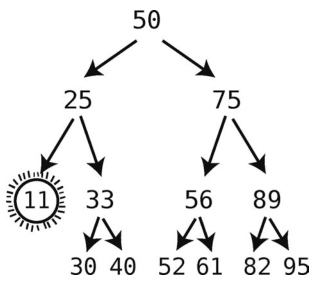
至此,删除操作遵循以下规则。
- 如果要删除的结点没有子结点,那直接删掉它就好。
- 如果要删除的结点有一个子结点,那删掉它之后,还要将子结点填到被删除结点的位置上。
要删除带有两个子结点的结点是最复杂的。比如说现在要删除56。
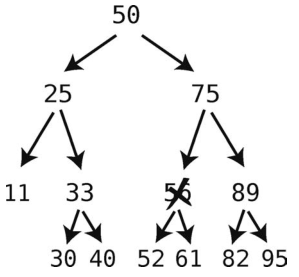
那52和61要怎么处理呢?显然不能将它们都放到 56原本的位置上,还需要第三条规则。
- 如果要删除的结点有两个子结点,则将该结点替换成其后继结点。一个结点的后继结点,就是所有比被删除结点大的子结点中,最小的那个。
上面这句话听起来有点绕。或者你把这些结点按顺序排好,那么每个结点后续的那个结点就是其后继结点。就像本例中56的所有后裔中,只有61能被称为其后继结点。按照这个规则,我们将56替换成61。

那计算机是怎么找出后继结点的呢?这是有算法可循的。
跳到被删除结点的右子结点,然后一路只往左子结点上跳,直到没有左子结点为止,则所停留的结点就是被删除节点的后继结点。
再来看一个更复杂的删除,这次我们删除根结点。
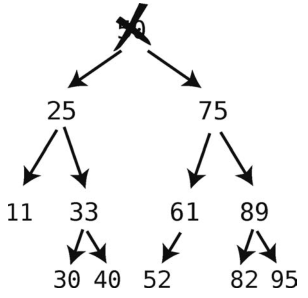
现在需要找后继结点来填补根的位置。
首先,访问右子结点,然后一路往左下方向移步,直至没有左子结点的结点上。
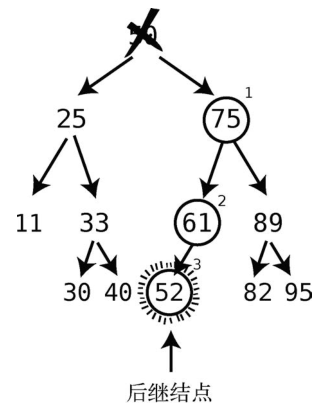
这就找出后继结点52了,接着我们将其填到被删除结点的位置上。
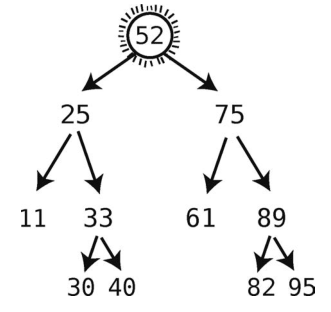
删除完成!
然而,还有一种情况我们没遇到过,那就是后继结点带有右子结点。让我们回到根被删除之前的状态,并且给52加上一个右子结点。
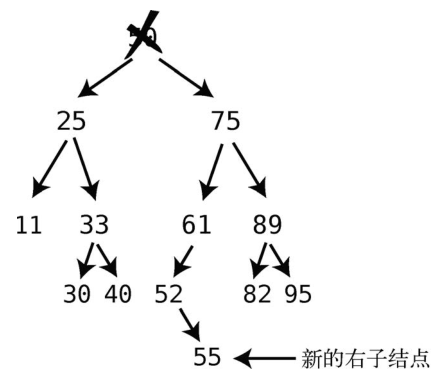
如此一来,就不能只将后继结点52移到根那里了,因为这样会使其子结点55悬空。于是,我们再加一条关于删除的规则。
- 如果后继结点带有右子结点,则在后继结点填补被删除结点以后,用此右子结点替代后继结点的父节点的左子结点。
下面运行一遍这个流程。
首先,将后继结点填到根处。
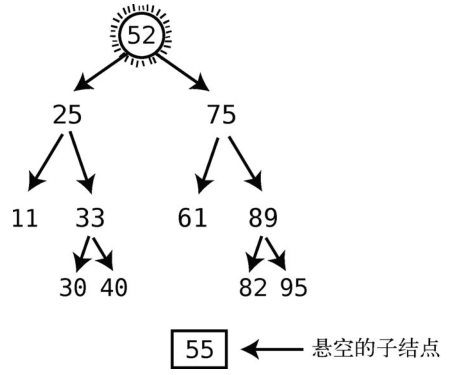
此时55便悬在半空中了。接下来,将55转换为继承节点的父节点的左子节点,本例中,61是继承结点的父结点,所以55成为61的左子结点。
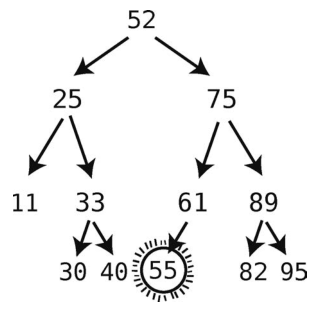
这才算真正完成了。
以下为二叉树的删除算法的所有规则。
- 如果要删除的结点没有子结点,那直接删掉它就好。
- 如果要删除的结点有一个子结点,那删掉它之后,还要将子结点填到被删除结点的位置上。
- 如果要删除的结点有两个子结点,则将该结点替换成其后继结点。一个结点的后继结点,就是所有比被删除结点大的子结点中,最小的那个。
- 如果后继结点带有右子结点,则在后继结点填补被删除结点以后,用此右子结点替代后继结点的父节点的左子结点。
以下是用Python写的二叉树递归式删除算法。为了易于理解,安插了一些注释进去。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46def delete(valueToDelete, node):
# 当前位置的上一层无子结点,已到达树的底层,即基准情形
if node is None:
return None
# 如果要删除的值小于(或大于)当前结点,
# 则以左子树(或右子树)为参数,递归调用本方法,
# 然后将当前结点的左链(或右链)指向返回的结点
elif valueToDelete < node.value:
node.leftChild = delete(valueToDelete, node.leftChild)
# 将当前结点(及其子树,如果存在的话)返回,
# 作为其父结点的新左子结点(或新右子结点)
return node
elif valueToDelete > node.value:
node.rightChild = delete(valueToDelete, node.rightChild)
return node
# 如果要删除的正是当前结点
elif valueToDelete == node.value:
# 如果当前结点没有左子结点,
# 则以右子结点(及其子树,如果存在的话)替换当前结点成为当前结点之父结点的新子结点
if node.leftChild is None:
return node.rightChild
# 如果当前结点没有左子结点,也没有右子结点,那这里就是返回 None
elif node.rightChild is None:
return node.leftChild
# 如果当前结点有两个子结点,则用 lift 函数(见下方)来做删除,
# 它会使当前结点的值变成其后继结点的值
else:
node.rightChild = lift(node.rightChild, node)
return node
def lift(node, nodeToDelete):
# 如果此函数的当前结点有左子结点,
# 则递归调用本函数,从左子树找出后继结点
if node.leftChild:
node.leftChild = lift(node.leftChild, nodeToDelete)
return node
# 如果此函数的当前结点无左子结点,
# 则代表当前结点是后继结点,于是将其值设置为被删除结点的新值
else:
nodeToDelete.value = node.value
# 用后继结点的右子结点替代后继结点的父节点的左子结点
return node.rightChild
跟查找和插入一样,平均情况下二叉树的删除效率也是O(log N)。因为删除包括一次查找,以及少量额外的步骤去处理悬空的子结点。有序数组的删除则由于需要左移元素去填补被删除元素产生的空隙,最终导致O(N)的时间复杂度。
二叉树实战
二叉树在查找、插入和删除上引以为傲的O(log N)效率,使其成为了存储和修改有序数据的一大利器。它尤其适用于需要经常改动的数据,虽然在查找上它跟有序数组不相伯仲,但在插入和删除方面,它迅速得多。
比如说你正在做一个书目维护的应用,它需要具备以下功能。
- 该应用可以将书名依照字母序打印。
- 该应用可以持续更新书目。
- 该应用可以让用户从书目中搜索书名。
如果你预期该书目不常变动的话,那么用有序数组作为存储结构是可以的。但这个应用偏偏要经常实时更新数据。要是其中包含上百万册图书,那还是用二叉树来保存比较好。
存储书名的二叉树大概是下面这个样子。
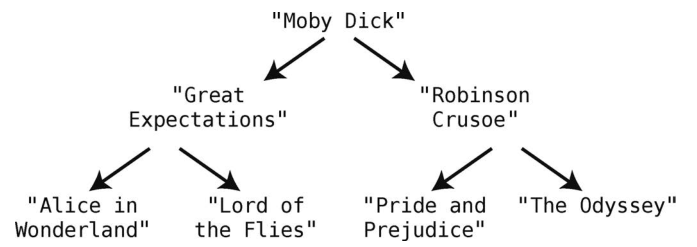
书名的搜索和更新,可以按我们之前介绍的二叉树查找、插入和删除来解决。但依照字母序打印书名该怎么做呢?
首先,我们得学会如何访问树上的所有结点。访问数据结构中所有元素的过程,叫作遍历数据结构。
接着,为了使书名以字母序打印,我们得确保遍历也是以字母序进行。虽然有多种方法可以遍历树,但对于这个要求字母序打印的应用,我们采用中序遍历。
递归是实施中序遍历的有力工具。我们将创建一个名为traverse的递归函数,它可以在任一结点上调用。然后执行以下步骤。
(1) 如果此结点有左子结点,则在左子结点上调用自身(traverse)。
(2) 访问此结点(对于书目应用来说,就是打印结点的值)。
(3) 如果此结点有右子结点,则在右子结点上调用自身(traverse)。
若当前结点没有子结点,则意味着该递归算法到达了基准情形,这时我们无须再调用traverse,只需打印结点中的书名就行了。
在“Moby Dick”上调用traverse的话,就能以下图的顺序访问树上的所有结点。
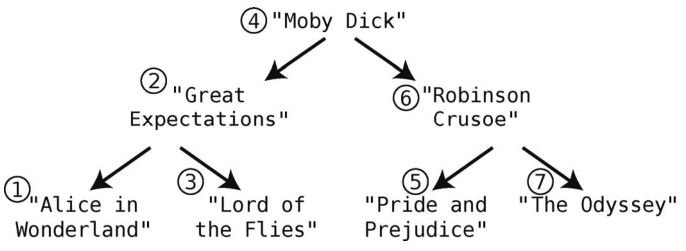
这样就能依照字母序打印书目了。遍历会访问树上所有的结点,所以树的遍历效率为O(N)。
以下是用Python写的以字母序打印书目的traverse_and_print函数。1
2
3
4
5
6def traverse_and_print(node):
if node is None:
return
traverse_and_print(node.leftChild)
print(node.value)
traverse_and_print(node.rightChild)
总结
二叉树是一种强大的基于结点的数据结构,它既能维持元素的顺序,又能快速地查找、插入和删除。尽管比它的近亲链表更为复杂,但它更有用。
值得一提的是,树形的数据结构除了二叉树以外还有很多种,包括堆、B树、红黑树、2-3-4树等。它们也各有自己适用的场景。
下一章,我们还会遇见另一种基于结点的数据结构--图。图是社交网络和地图软件等复杂应用的核心组成部分,强大且灵活。