思考并回答以下问题:
- 什么是图?怎么用代码表示图?每个顶点都是一个对象,维护一个列表。怎么理解?
- 什么是顶点?什么是边?怎么才叫相邻?
- 什么是有向图?什么是无向图?
- 什么是二度联系人?
- 什么是广度优先搜索?
- 什么是加权图?要往图里加上权重,要把表示邻接点的数组换成散列表。怎么换?
- 以二维数组来保存朋友关系会在查询a的朋友时有什么问题?
- 遍历图还需要一个队列。怎么理解?
- Neo4j是什么软件?
本章涵盖:
- 图
- 广度优先搜索
- 图数据库
- 加权图
- Dijkstra算法
假设我们正在打造一个像Facebook那样的社交网络。在该应用里,大家可以加别人为“朋友”。这种朋友关系是相互的,如果Alice是Bob的朋友,那么Bob也会是Alice的朋友。
这些关系数据要怎么管理才好呢?
一种简单的方法是,以二维数组来保存每一对关系。1
2
3
4
5
6
7
8
9relationships = [
["Alice", "Bob"],
["Bob", "Cynthia"],
["Alice", "Diana"],
["Bob", "Diana"],
["Elise", "Fred"],
["Diana", "Fred"],
["Fred", "Alice"]
]
不幸的是,这样无法快速地知道Alice的朋友是哪些人。你只能在数组里按逐对关系检查,看Alice在不在那对关系中。在检查过程中,你还得创建一个列表来暂存查出的朋友(此例中有Bob、Diana和Fred)。
由于数据以这种结构存储,若想查找Alice的朋友就得检查数据库中的所有关系,需要O(N)的时间复杂度。
其实有一种更好的存储方法。使用图这种数据结构的话,我们可以在O(1)时间内找出Alice的所有朋友。
图
图是一种善于处理关系型数据的数据结构,使用它可以很轻松地表示数据之间是如何关联的。
下图是我们的Facebook网络。
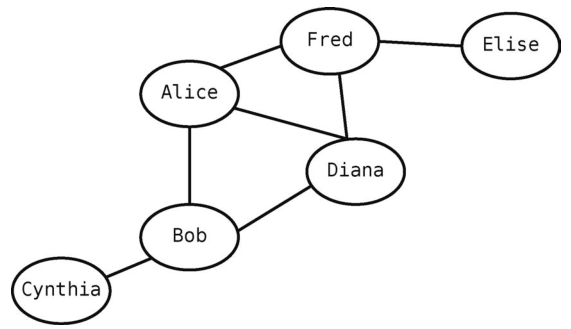
每个人都是一个结点,人与人之间的朋友关系则以线段表示。按照图的术语来说,每个结点都是一个顶点,每条线段都是一条边。当两个顶点通过一条边联系在一起时,我们会说这两个顶点是相邻的。
图的实现形式有很多,最简单的方法之一就是用散列表。例如,使用Ruby散列表来实现一个极为基础的社交网络。1
2
3
4
5
6
7
8friends = {
"Alice" => ["Bob", "Diana", "Fred"],
"Bob" => ["Alice", "Cynthia", "Diana"],
"Cynthia" => ["Bob"],
"Diana" => ["Alice", "Bob", "Fred"],
"Elise" => ["Fred"],
"Fred" => ["Alice", "Diana", "Elise"]
}
因为从散列表里查找一个键所对应的值只需要1步,所以查找Alice的朋友能以O(1)的时间复杂度完成,如下所示。1
friends["Alice"]
跟Facebook不同,Twitter里面的关系不是相互的。Alice可以关注Bob,但Bob不一定要关注Alice。让我们构造一个新的图来表示谁关注了谁。
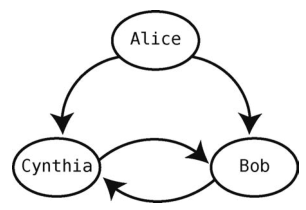
图中箭头表示了关系的方向。Alice关注了Bob和Cynthia,但没有人关注Alice。Bob和Cynthia互相关注。
用散列表来表示的话,就是这样:1
2
3
4
5followees = {
"Alice" => ["Bob", "Cynthia"],
"Bob" => ["Cynthia"],
"Cynthia" => ["Bob"]
}
虽然Facebook跟Twitter的例子很相似,但它们本质上是不一样的。Twitter中的关系是单向的,我们也在图中用箭头表示了其方向,因此它的图是有向图。Facebook中的关系则是相互的,我们只画成了普通的线段,它的图是无向图。
尽管只用散列表也可以实现一个图,但是以面向对象的方法来写会更加健壮。
以下便是一种更为健壮的实现方式,它采用的语言是Ruby。1
2
3
4
5
6
7
8
9
10
11
12class Person
attr_accessor :name, :friends
def initialize(name)
@name = name
@friends = []
end
def add_friend(friend)
@friends << friend # 数组添加对象元素
end
end
1 | class Person |
有了这个Ruby类,我们就可以创建人物并且给他们添加朋友了。1
2
3
4mary = Person.new("Mary")
peter = Person.new("Peter")
mary.add_friend(peter)
peter.add_friend(mary)
1 | $mary = new Person('Mary'); |
广度优先搜索
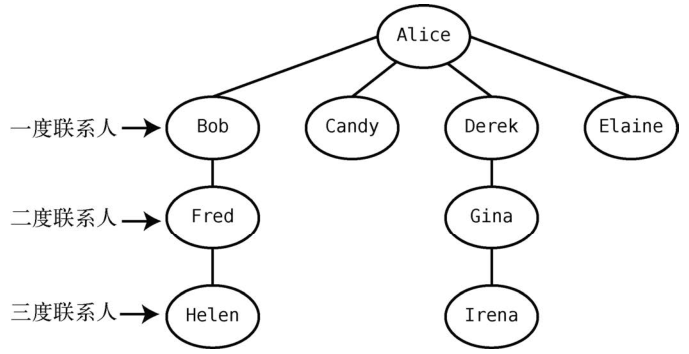
LinkedIn也是一个流行的社交网络,其专注于职业社交。LinkedIn的一个有名的功能就是,你除了能够看到自己直接添加的联系人,还可以发掘你的二度、三度联系人。
如图所示,Alice能直接联系到Bob,Bob能直接联系到Cynthia。但Alice无法直接联系到Cynthia。由于她们之间的联系要经过Bob,因此Cynthia是Alice的二度联系人。

如果我们想查看Alice的整个关系网,包括她那些间接的关系,需要怎么做呢?
图有两种经典的遍历方式:广度优先搜索和深度优先搜索。在此我们会研究广度优先搜索,深度优先搜索你可以自己去学习。两者是相似的,并且在大多数情况下都一样好用。
广度优先搜索算法需要用队列(参见队列)来记录后续要处理哪些顶点。该队列最初只含有起步的顶点(对本例来说,就是Alice)。于是算法一开始,我们的队列如下所示。
[Alice]
然后处理Alice顶点。我们将其移出队列,标为“已访问”,并记为当前顶点。(很快我们就会走一遍整个流程,让你看得更明白一些。)
接着按照以下3步去做。
(1)找出当前顶点的所有邻接点。如果有哪个是没访问过的,就把它标为“已访问”,并且将它入队。(尽管该顶点并未作为“当前顶点”被访问过。)
(2) 如果当前顶点没有未访问的邻接点,且队列不为空,那就再从队列中移出一个顶点作为当前顶点。
(3) 如果当前顶点没有未访问的邻接点,且队列里也没有其他顶点,那么算法完成。
下面来实际演示一遍。Alice的LinkedIn关系网如下图所示。
首先,将Alice设为当前顶点。为了在图中表示她是当前顶点,我们用线段将其围绕。为了表示Alice已被访问,我们在她旁边打了个钩。继续该算法,找出一个未访问的邻接点--本例中的Bob,在他名字旁边打个钩,如下图所示。
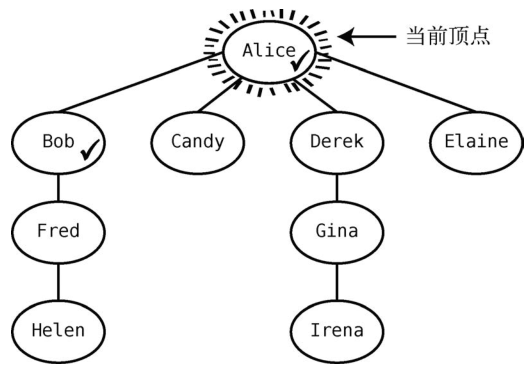
我们也将Bob入队,使队列变为[Bob]。这意味着Bob未曾作为当前顶点。注意,虽然当前顶点是Alice,但我们也能访问Bob。
接着,检查当前顶点Alice是否还有未访问的邻接点。发现有Candy,于是将其标为已访问。
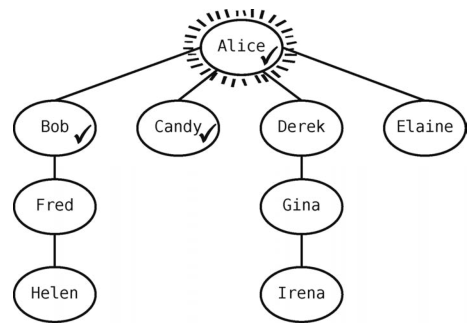
现在队列为[Bob, Candy] 。
Alice还有邻接点Derek没访问过,于是访问他。
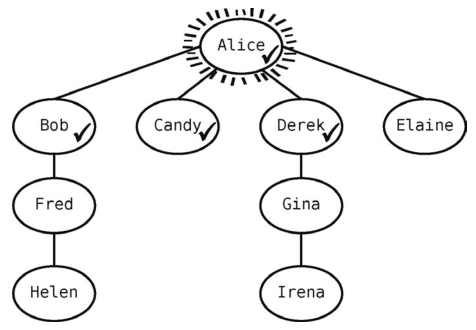
现在队列为[Bob, Candy, Derek] 。
Alice还有一个未访问的关系Elaine,于是我们也要访问她。
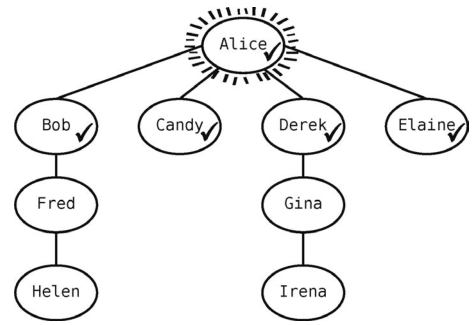
现在队列为[Bob, Candy, Derek, Elaine] 。
因为Alice已经没有未访问的邻接点了,所以执行本算法的第2条规则,从队列里移出一个顶点,把它设为当前顶点。回想第8章提到的,队列只能在队头移除数据,于是现在要移出的就是Bob。
现在队列变为[Candy, Derek, Elaine],Bob成为了当前顶点。
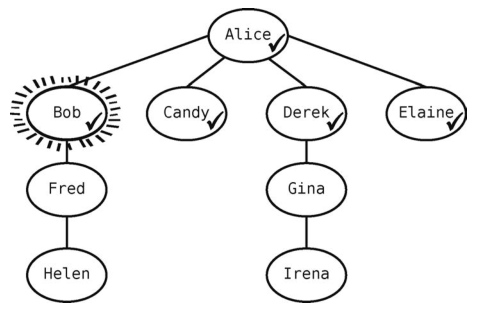
然后回到第1条规则,找出当前顶点的所有未访问的邻接点。Bob有一个邻接点Fred,于是将他标记为已访问,并把他加入队列。
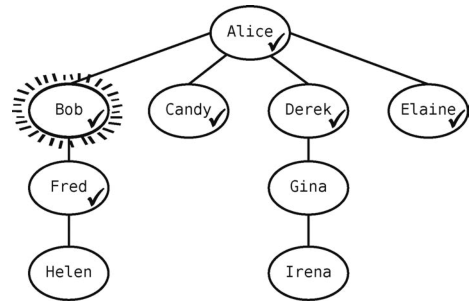
现在队列为[Candy, Derek, Elaine, Fred]。
因为Bob没有其他未访问的邻接点了,所以出队一个顶点--Candy--作为当前顶点。
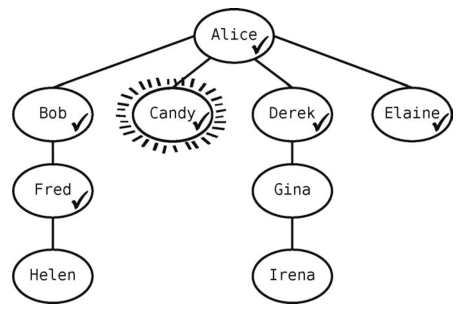
然而Candy没有未访问的邻接点。于是再从队列中拿出一个顶点--Derek--使得队列变成[Elaine, Fred]。
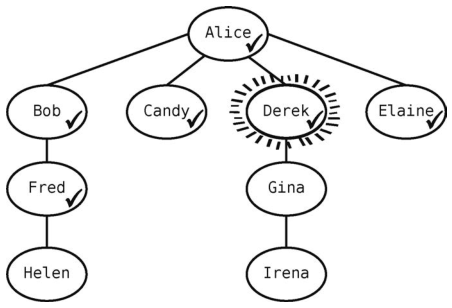
Derek有一个未访问的邻接点Gina,我们将其标记为已访问。
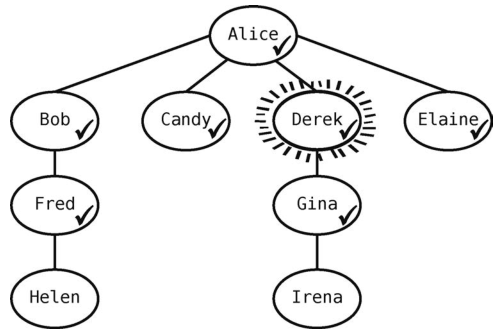
现在队列为[Elaine, Fred, Gina]。
Derek没有邻接点需要访问了,于是我们从队列里拿出Elaine,将她标记为当前顶点。
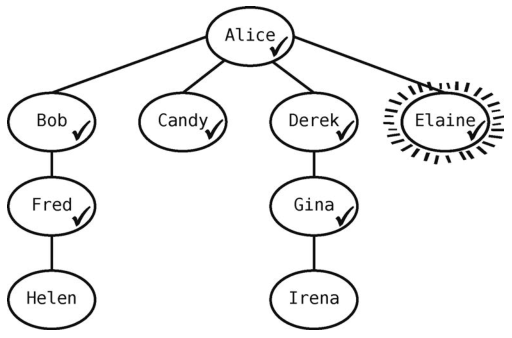
Elaine没有未访问的邻接点,于是从队列中拿出Fred。
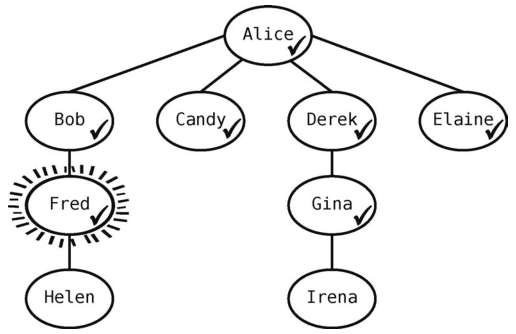
此时队列变为[Gina]。
Fred有一个联系人要访问--Helen--于是将其标为已访问,并且入队,使队列变成[Gina, Helen]。
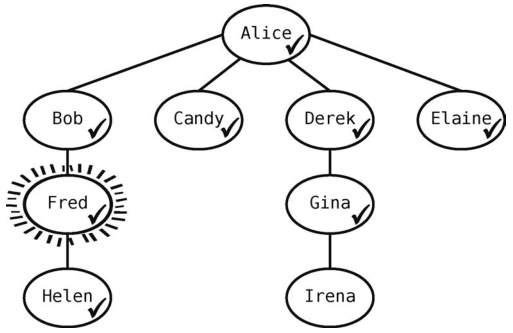
Fred已经没有未访问的关系了,所以我们将Gina移出队列,将她设为当前顶点。
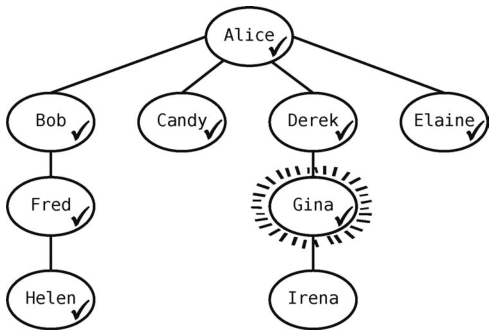
现在队列里只剩[Helen]了。
Gina有一个邻接点要访问--Irena。
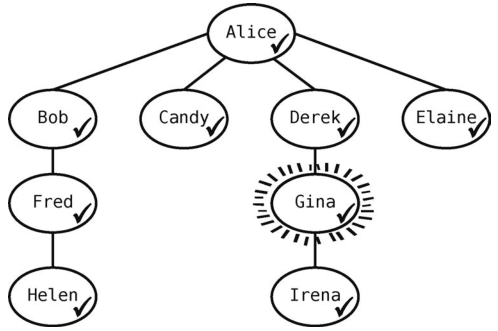
现在队列为[Helen, Irena]。
Gina没有其他关系需要访问了,所以让Helen出队,将她设为当前顶点,于是队列里剩下的是[Irena]。Helen没有什么人需要访问,于是我们让Irena出队,将她设为当前顶点。因为Irena没有顶点需要访问,而且队列空了,所以算法结束!
我们在Person类里加上display_network方法,以广度优先搜索的方式展示一个人的关系网里所有的名字。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39class Person
attr_accessor :name, :friends, :visited # visited表示是否标记
def initialize(name)
@name = name
@friends = []
@visited = false
end
def add_friend(friend)
@friends << friend
end
def display_network
# 记下每个访问过的人,以便算法完结后能重置他们的 visited 属性为 false
to_reset = [self]
# 创建一个开始就含有根顶点的队列
queue = [self]
self.visited = true
while queue.any?
# 设出队的顶点为当前顶点
current_vertex = queue.shift
puts current_vertex.name
# 将当前顶点的所有未访问的邻接点加入队列
current_vertex.friends.each do |friend|
if !friend.visited
to_reset << friend
queue << friend
friend.visited = true
end
end
end
# 算法完结时,将访问过的结点的 visited 属性重置为 false
to_reset.each do |node|
node.visited = false
end
end
end
1 | class Person |
为了使它运作起来,我们还给Person类增加了visited属性,来记录一个人在本次搜索中是否已被访问。
将算法的步骤分为两类之后,我们可以看出图的广度优先搜索的效率。
- 让顶点出队,将其设为当前顶点。
- 访问每个顶点的邻接点。
这样看来,每个顶点都会有一次出队的经历。以大O记法表示,就是O(V),意思是有V个顶点,就有V次出队。
既然要处理N个顶点,不应该表示为O(N)吗?不是的,因为在此算法(以及很多其他图的算法)中,除了处理顶点本身,还得处理边,下面就来解释。
我们观察一下访问邻接点需要多少步。
以当前顶点为Bob的时候为例。
此时我们会运行如下代码。1
2
3
4
5
6current_vertex.friends.each do |friend|
if !friend.visited
queue << friend
friend.visited = true
end
end
1 | foreach ($current_vertex->friends as $friend) |
就是说,我们会访问Bob所有的邻接点,其中不但有Fred,还有Alice!尽管她曾被访问过,不用再入队,但访问她还是增加了一次each循环。
要是你再认真地运行一遍整个广度优先搜索的流程,你会发现访问邻接点所用的步数,是图中边数的两倍。因为一条边连接着两个顶点,对于每个顶点,我们都要访问其所有邻接点。所以每条边都会被使用两次。
因此,有E条边,就会有2E步来访问邻接点,即每对邻接点都会被访问两次。不过由于大O忽略常数,所以只写作O(E)。
因为广度优先搜索有O(V)次出队,还有O(E)次访问,所以我们说它的效率为O(V + E)。
图数据库
因为图擅长处理关系信息,所以有些数据库就以图的形式来存储数据。传统的关系型数据库(以行和列的形式保存数据的数据库)也能存储这类信息,我们不妨比较一下它们处理社交网络之类的数据时的表现。
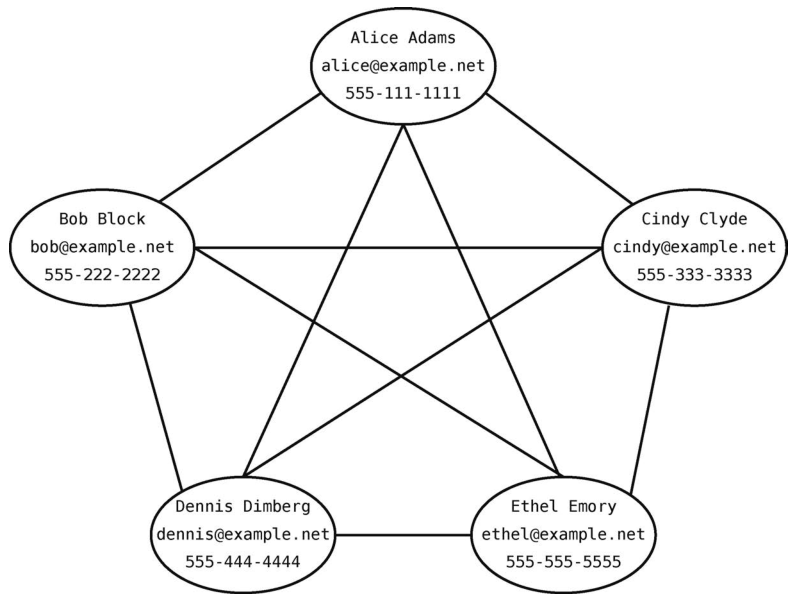
假设有一个5人的社交网络,分别是Alice、Bob、Cindy、Dennis和Ethel,他们互相都有联系。保存他们个人信息的图数据库大概会如下图所示。
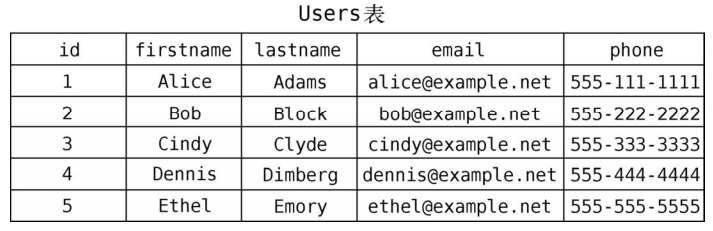
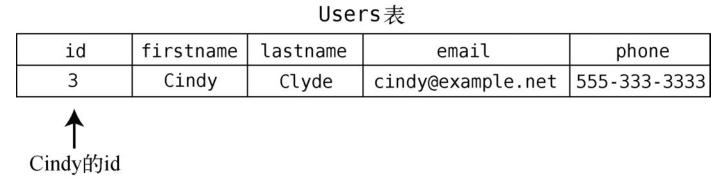
这种信息也可以用关系型数据库来存储。那得需要两张表--一张保存个人信息,另一张保存朋友关系。以下是Users表。
另一张Friendships表记录着谁是谁的朋友。
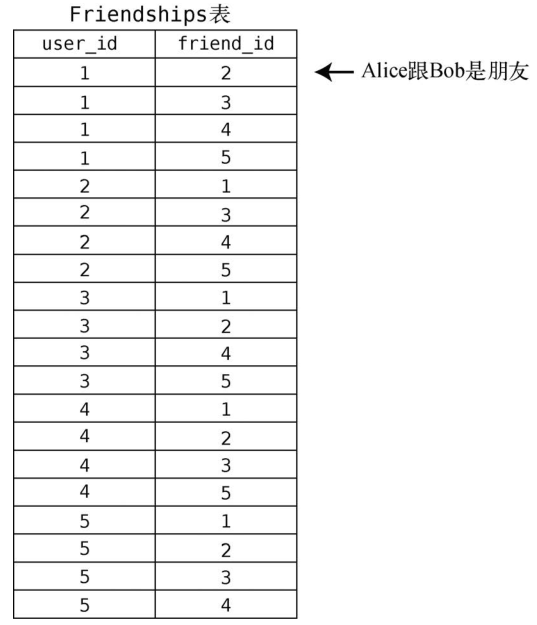
我们不会太过深入地研究数据库理论,但你得知道在Friendships表中只需以用户id来指代用户。
如果这个社交网络允许用户查看其朋友的全部信息,而Cindy也正要这么做,那意味着她想看到一切关于Alice、Bob、Dennis和Ethel的信息,包括他们的邮件地址和电话号码。
那我们就来看看以关系型数据库为后端的应用会怎样执行她的请求。首先,我们得找出User表中Cindy的id。
然后,找出Friendships表中所有user_id为3的行。
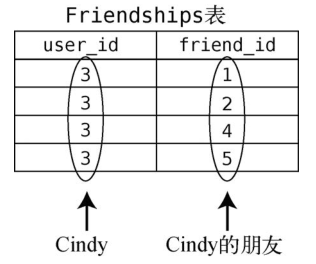
我们就得到了Cindy朋友的id列表:[1, 2, 4, 5]。
有了id列表之后,我们还得回Users表找出这些id对应的行。计算机从Users表查找一行的速度大概是O(log N)。因为数据库中的行会按照id的顺序来维护,所以我们可以用二分查找来找出id对应的行。(以上解释只适用于部分关系型数据库,其他关系型数据库可能有不同做法。)
Cindy有4个朋友,所以计算机需要做4次O(log N)查询才能提取出她全部朋友的个人信息。推广开来,若有M个朋友,那么提取他们个人信息的效率就为O(M log N)。换句话说,对于每个朋友,都要执行一次步数为log N的搜索。
相比之下,后端为图数据库时,一旦在数据库中定位到Cindy,那么只需一步就能查到她任一朋友的信息。因为数据库中的每个顶点已经包含了该用户的所有信息,所以你只需遍历那些连接Cindy与朋友的边即可。如下图所示,总共也就4步。
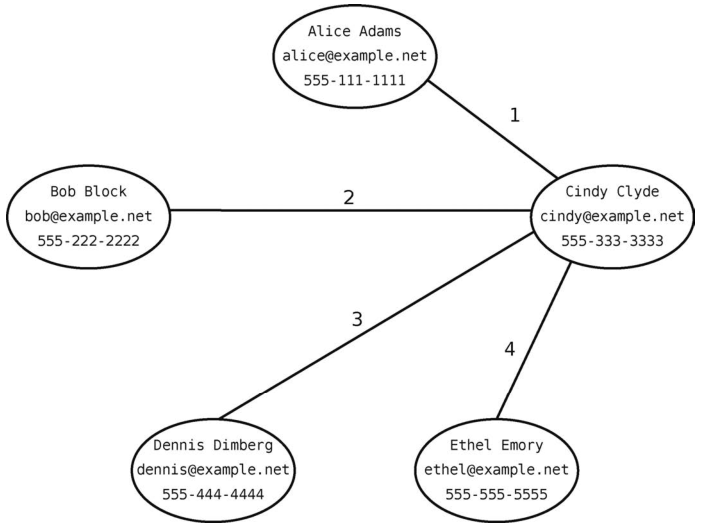
用图数据库的话,有N个朋友就需要O(N)步去获取他们的数据。与关系型数据库的O(M log N)相比,确实是极大的效率提升。
Neo4j是开源的图数据库中比较受欢迎的一个。我建议你上它的官网去了解更多关于图数据库的知识。其他开源的图数据库还有ArangoDB和Apache Giraph。
但记住,图数据库也并不总是最好的解决方案。你得谨慎地评估每个应用场景的需求再做选择。
加权图
还有一种图叫作加权图。它跟普通的图类似,但边上带有信息。
以下这个包含了美国几个主要城市的简陋地图,就是一个加权图。
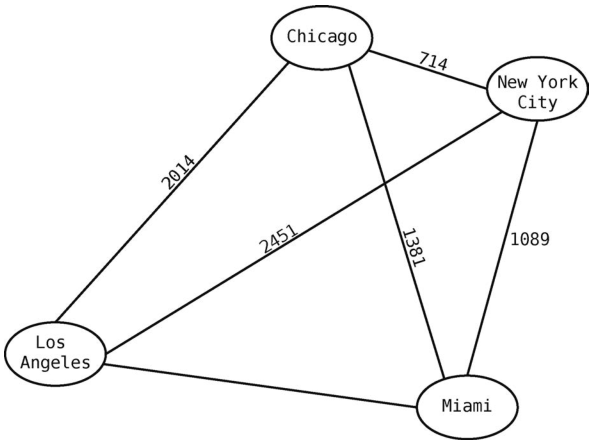
此图中,每条边上都有一个数字,它表示那条边所连接的两个城市相距多少英里。例如,Chicago和New York City之间的距离为714英里。
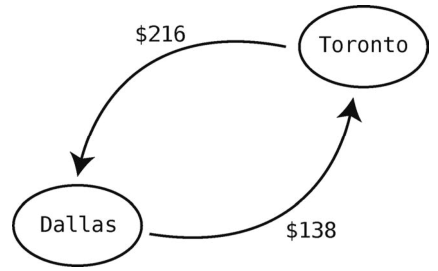
加权图可以是有方向的。以下图为例,尽管从Dallas飞到Toronto只要138美元,但从Toronto飞到Dallas要216美元。
要往图里加上权重,得稍微更改一下我们的Ruby代码。具体来说,我们要把表示邻接点的数组换成散列表。对于上图来说,一个顶点就是一个City类的对象。1
2
3
4
5
6
7
8
9
10
11
12
13class City
attr_accessor :name, :routes
def initialize(name)
@name = name
# 把表示邻接点的数组换成散列表
@routes = {}
end
def add_route(city, price)
@routes[city] = price
end
end
这样就可以创建城市和不同价格的航线了。1
2
3
4dallas = City.new("Dallas")
toronto = City.new("Toronto")
dallas.add_route(toronto, 138)
toronto.add_route(dallas, 216)
我们可以借助加权图来解决最短路径问题。
下图展示了5个城市之间的航线价格。
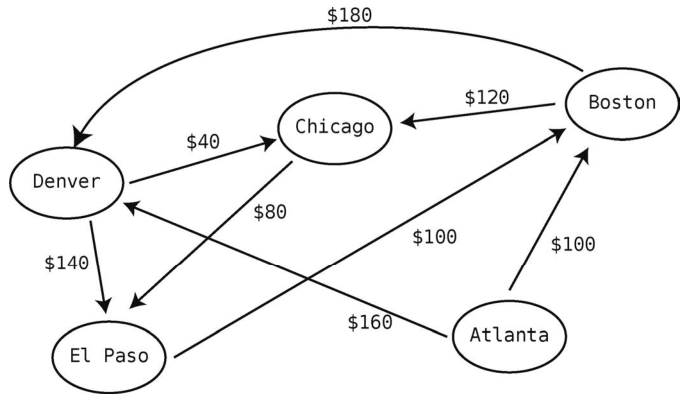
假设我目前身在Atlanta,想飞去El Paso。不幸的是,现在没有直达航班。然而,我也可以在其他城市转机过去。例如,先从Atlanta到Denver,再从Denver到El Paso。这会花费300美元。但再看仔细一点,你会发现从Atlanta沿Denver、Chicago再到ElPaso会更加便宜。虽然多转一次,但只需花280美元。
这就是一种最短路径问题:如何以最低的价钱从Atlanta飞往El Paso。
Dijkstra算法
解决最短路径问题的算法有好几种,其中一种有趣的算法是由Edsger Dijkstra于1959年发现的。该算法也很自然地被称为Dijkstra算法。
Dijkstra算法的规则如下(别担心,之后我们跟着例子运行一遍就会更明白了)。
- (1)以起步的顶点为当前顶点。
- (2)检查当前顶点的所有邻接点,计算起点到所有已知顶点的权重,并记录下来。
- (3)从未访问过(未曾作为当前顶点)的邻接点中,选取一个起点能到达的总权重最小的顶点,作为下一个当前顶点。
- (4)重复前3步,直至图中所有顶点都被访问过。
下面来一步步地运行一遍整个算法。
我们用以下表格来记录Atlanta到其他城市最便宜的价格。
首先,以起步顶点(Atlanta)作为当前顶点。此时我们能访问的就是当前顶点以及其邻接点。为指明哪个点是当前顶点,我们以线段将其围绕。为指明哪些点曾作为当前顶点,我们给它们打上钩。
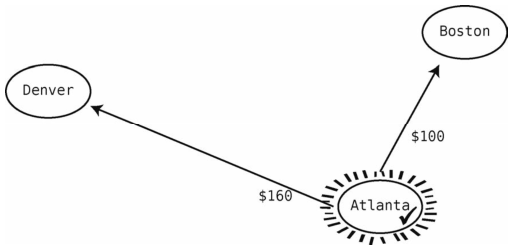
接着检查所有邻接点,记下从起点(Atlanta)到所有已知地点的权重。可见从Atlanta到Boston是100美元,从Atlanta到Denver是160美元,于是记录到表格里。
接着从Atlanta可到达但又未访问过的顶点中,找出最便宜的那个。就目前所知,从Atlanta出发可以到达Boston和Denver,并且Boston(100美元)比Denver(160美元)更便宜。因此,选择Boston作为当前顶点。
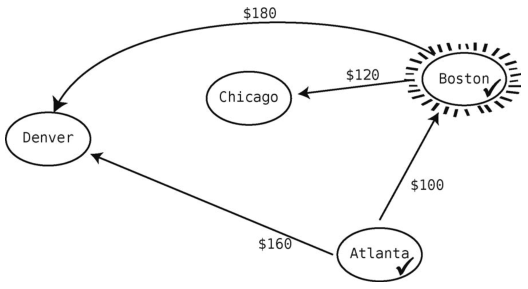
然后检查从Boston出发的航线,更新从起点Atlanta到所有已知地点的花费。我们看到Boston到Chicago是120美元。Atlanta到Boston是100美元,Boston到Chicago是120美元,所以从Atlanta到Chicago最便宜的(而且是目前唯一的)路线要220美元。我们把它记在表里。
再看看从Boston出发的另一条航线--Denver--要180美元。于是我们又发现了一条从Atlanta到Denver的路线:Atlanta到Boston再到Denver。不过这条路线要280美元,而Atlanta直飞Denver才160美元,所以无须更新价格表,毕竟我们只想记录最便宜的路线。
既然从当前顶点(Boston)出发的航线都已探索过了,就得找下一个从起点Atlanta所能到达的最便宜的未访点了。根据表格来看,最便宜的还是Boston,但它已经打过钩了。这样最便宜的未访问城市应该是Denver了,因为与220美元的Chicago相比,它只要160美元。于是Denver变成了当前顶点。
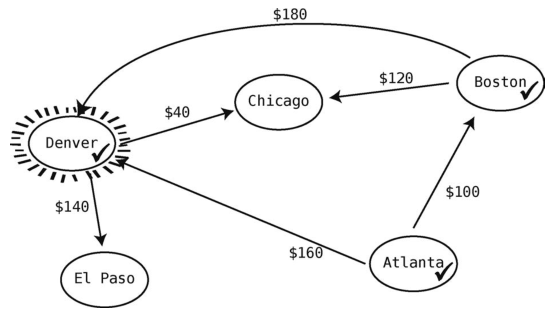
那么我们就来观察由Denver出发的航线,其中一条从Denver到Chicago的航线是40美元。于是我们可以更新Atlanta到Chicago的最低价格了。因为现在的价格表里Atlanta到Chicago要220美元,但若经Denver转机,则只需200美元。所以更新一下表格。
从Denver飞出的航班还有一个,它的目的地是El Paso。我们要计算Atlanta到El Paso的最低价格,目前只能从Atlanta到Denver再到El Paso,共300美元。将价钱记下。
现在还没访问的顶点有两个:Chicago和El Paso。Atlanta到Chicago的最低价(200美元)比Atlanta到El Paso的最低价(300美元)要低,所以下一步选择Chicago作为当前顶点。
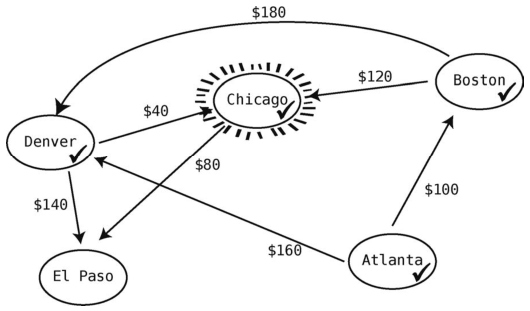
Chicago只有一个出发航班:80美元到El Paso。于是Atlanta到El Paso路线的最低价格得以更新:从Atlanta到Denver,再到Chicago,最后抵达El Paso,总共花费280美元。我们把它记下。
最后只剩一个城市可作为当前顶点了,那就是El Paso。
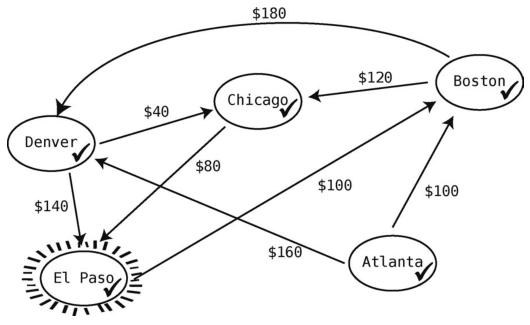
El Paso只有一个出发航班:100美元飞到Boston。这并没刷新Atlanta到其他地方的最低价,所以我们无须更新价格表。
现在所有顶点都访问过了,这就意味着Atlanta到其他城市的所有路径都已发掘。于是算法结束,我们也可以从价格表得知从Atlanta到地图上任一城市的最低价格了。
以下是Dijkstra算法的Ruby实现。
我们先创建一个代表城市的Ruby类。一个城市就是图上的一个结点,它记有自己的名字以及可到达的城市。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class City
attr_accessor :name, :routes
def initialize(name)
@name = name
# 把表示邻接点的数组换成散列表
@routes = {}
# 如果此城市是 Atlanta,则散列表应包含:
# {boston => 100, denver => 160}
end
def add_route(city, price_info)
@routes[city] = price_info
end
end
然后用add_route来建立城市间的航线。1
2
3
4
5
6
7
8
9
10
11
12atlanta = City.new("Atlanta")
boston = City.new("Boston")
chicago = City.new("Chicago")
denver = City.new("Denver")
el_paso = City.new("El Paso")
atlanta.add_route(boston, 100)
atlanta.add_route(denver, 160)
boston.add_route(chicago, 120)
boston.add_route(denver, 180)
chicago.add_route(el_paso, 80)
denver.add_route(chicago, 40)
denver.add_route(el_paso, 140)
Dijkstra算法的代码是有点复杂的,所以我在每一步都做了注释。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55def dijkstra(starting_city, other_cities)
# 散列表 routes_from_city 用来保存从给定城市到其他所有城市的价格
# 以及途经的城市
routes_from_city = {}
# 它的格式如下:
# {终点城市 => [价格, 到达终点城市前所要经过的那个城市]}
# 以上图为例,此散列表最后会是:
# {atlanta => [0, nil], boston => [100, atlanta], chicago => [200, denver],
# denver => [160, atlanta], el_paso => [280, chicago]}
# 从起点城市到起点城市是免费的
routes_from_city[starting_city] = [0, staring_city]
# 初始化该散列表时,因为去往所有其他城市的花费都未知,所以先设为无限
other_cities.each do |city|
routes_from_city[city] = [Float::INFINITY, nil]
end
# 以上图为例,此散列表起初会是:
# {atlanta => [0, nil], boston => [Float::INFINITY, nil],
# chicago => [Float::INFINITY, nil],
# denver => [Float::INFINITY, nil], el_paso => [Float::INFINITY, nil]}
# 已访问的城市记录在这个数组里
visited_cities = []
# 一开始先访问起点城市,将 current_city 设为它
current_city = starting_city
# 进入算法的核心逻辑,循环访问每个城市
while current_city
# 正式访问当前城市
visited_cities << current_city
# 检查从当前城市出发的每条航线
current_city.routes.each do |city, price_info|
# 如果起点城市到其他城市的价格比 routes_from_city 所记录的更低,
# 则更新记录
if routes_from_city[city][0] > price_info +
routes_from_city[current_city][0]
routes_from_city[city] =
[price_info + routes_from_city[current_city][0], current_city]
end
end
# 决定下一个要访问的城市
current_city = nil
cheapest_route_from_current_city = Float::INFINITY
# 检查所有已记录的路线
routes_from_city.each do |city, price_info|
# 在未访问的城市中找出最便宜的那个,
# 设为下一个要访问的城市
if price_info[0] < cheapest_route_from_current_city &&
!visited_cities.include?(city)
cheapest_route_from_current_city = price_info[0]
current_city = city
end
end
end
return routes_from_city
end
该方法可以这样使用:1
2
3
4routes = dijkstra(atlanta, [boston, chicago, denver, el_paso])
routes.each do |city, price_info|
p "#{city.name}: #{price_info[0]}"
end
虽然这个例子是找出最便宜的航线,但其解决方法也适用于地图软件和GPS技术。如果边上的权重不是表示价格,而是表示行车用时,那就可以用Dijkstra算法来确定从一个城市去另一个城市应该走哪条路线。
总结
这一章讲的是本书最后一种重要的数据结构,我们的学习之旅也接近了尾声。我们知道了图是处理关系型数据的强大工具,它除了能让代码跑得更快,还能帮忙解决一些复杂的问题。
学习至今,我们关注的主要是代码运行的速度。我们以时间和算法的步数来衡量代码的性能。
然而,性能的衡量方法不止这些。在某些情况下,还有比速度更重要的东西,比如我们可能更关心一种数据结构或算法会消耗多少内存。下一章,我们就来学习如何分析一段代码在空间上的效率。