思考并回答以下问题：

向量的基本运算包括哪些？

本章涵盖：

用Unity引擎开发游戏就是在引擎的上层再封装一层游戏架构，在游戏开发的逻辑中需要根据需求重新封装一些数学算法以便于逻辑调用。

Unity坐标系

3D坐标系表示的是三维空间，3D坐标系存在三个坐标轴，分别为x轴、y轴、z轴，如图1-1所示。

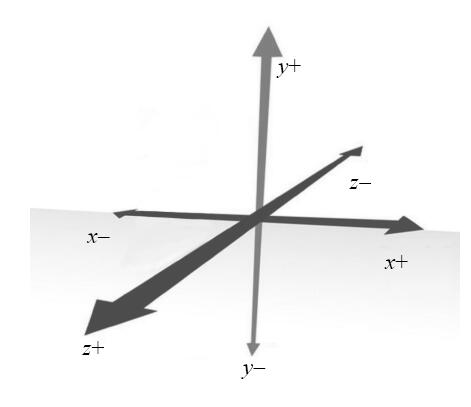
3D坐标系分为左手坐标系和右手坐标系。Unity使用的是左手坐标系。

Unity引擎的左手坐标系也被称为世界坐标系，做游戏开发时需要美工制作美术模型，运用MAX工具把建好的模型放到游戏场景中。在默认情况下，局部坐标和世界坐标系的原点是重合的，不能把所有的模型都叠加在世界坐标系的原点上，因此需要移动模型。模型移动时就会发生模型的局部坐标到世界坐标的转换，这个移动过程就是把模型的局部坐标转化成世界坐标。只是这个转化过程是在引擎编辑器内部实现的，实际上它就是将模型的各个点与世界矩阵相乘得到的。

Unity编辑器中的物体都在世界坐标系里面，比如我们通常使用的函数transform.position，它就是获取到当前物体的世界坐标位置，用户无须自己去计算，因为引擎内部已经计算好了。明白了原理后，再使用编辑器解决问题更有助于理解，做到知其然且知其所以然。如果要获取物体自身的坐标，也就是局部坐标，可以使用函数transform.localPosition获取当前模型的局部坐标。

用Unity引擎开发移动端手游会经常用到屏幕坐标系，屏幕坐标系就是通常使用的电脑屏幕，它是以像素为单位的，屏幕左下角为（0, 0）点，右上角为（Screen.Width, Screen.Height）点，Z的位置是根据相机的Z缓存值确定的。通常使用鼠标在屏幕上单击物体，它就是屏幕坐标。通过函数Input.mousePosition可以获得鼠标位置的坐标。我们使用的虚拟摇杆可以在屏幕上滑动，它也是屏幕坐标，可以通过函数Input.GetTouch(0).position获取到手指触摸屏幕坐标。

在游戏开发中，比如单击场景中的3D物体就需要从屏幕上发射一条射线与物体的包围盒相交，用于判断是否选中物体，对于UI的操作也都是基于屏幕坐标系的。

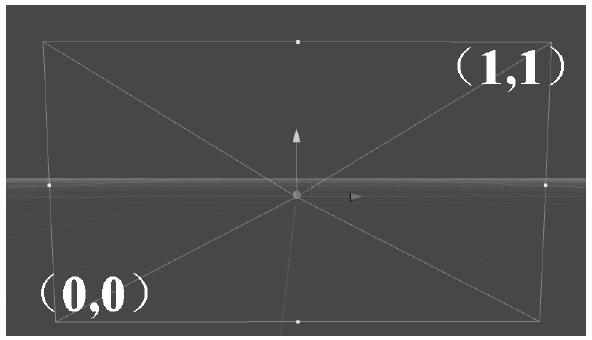
通过相机才能看到虚拟世界的物体。相机有自己的视口坐标，物体要转换到视口坐标才能被看到。相机的视口左下角为（0, 0）点，右上角为（1, 1）点，Z的位置是以相机的世界单位来衡量的。（0, 0）点和（1, 1）点是通过公式进行缩放计算的，这里面存在一个变换，读者了解就可以了。这也是为什么视口的大小通常都是（0, 0）和（1, 1），效果如图1-2所示，图的中心点是摄像机。

下面介绍世界坐标、屏幕坐标、相机坐标之间的转换方式。举一个简单的例子，在一个空场景里面放置一个立方体，物体在编辑器中也就是世界坐标系中的摆放如图1-3所示。

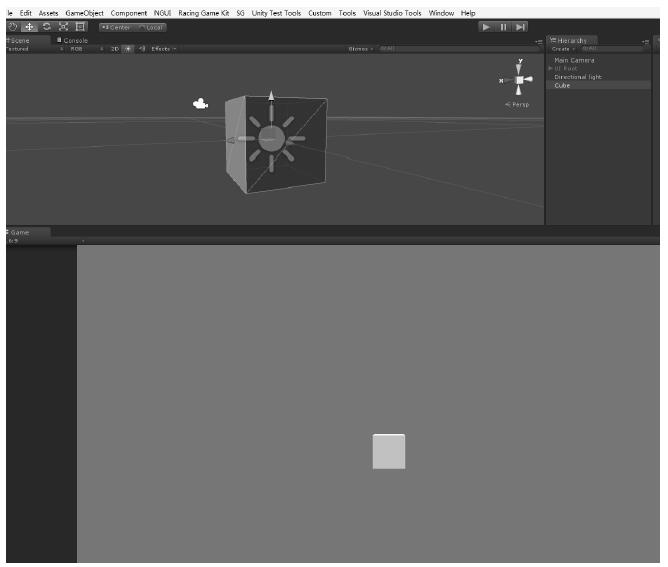
获取物体位置的通常写法是transform.position，它表示的是立方体在3D世界中的世界坐标的位置。如果使用的是触摸屏幕，那么可以通过函数Input.GetTouch(0).position获取到屏幕坐标。它们之间的转换方式如下。

世界坐标到屏幕坐标的转化函数：camera.WorldToScreenPoint(transform.position)。
屏幕坐标到视口坐标的转化函数：camera.ScreenToViewportPoint(Input.GetTouch(0).position)。
世界坐标到视口坐标的转化函数：camera.WorldToViewportPoint(obj.transform.position)。

这些转换也是固定流水线的矩阵变换，只是Unity将其封装好了而已。如果想学习固定流水线，可以参考《手把手教你架构3D游戏引擎》一书，里面有固定流水线的详细讲解，下面介绍向量运算。

向量

向量的基本运算包括加法、减法、点乘、叉乘、单位化运算等，其中减法、点乘、叉乘、单位化运算在游戏开发中使用得最为广泛。

首先介绍一下向量，向量的表示如图1-4所示。

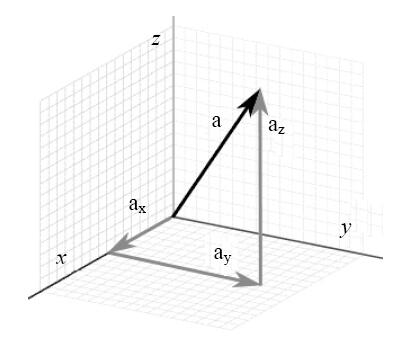
向量是具有方向和长度的矢量，它并不是一条射线，向量有2D、3D、4D等的。在游戏开发里面一般使用的是2D向量和3D向量。2D向量表示为两个数值，而3D向量是由三个数值表示的。3D游戏开发中经常使用的3D向量的几何表示如图1-5所示。

图中向量a在3D坐标系中用三个值表示：，下面介绍向量的加法运算。

向量的加法

顾名思义，向量的加法就是两个向量相加，几何表示如图1-6所示。

图1-6是两个向量相加的示意图，二者相加后得到的值还是一个向量，其运算方法就是两个向量对应项的相加。向量的加法在游戏开发中一般表示物体从一个位置移动到另一个位置，如图1-7所示。

图1-6　向量加法的几何表示

图1-7　向量的加法在游戏中的表示

如果立方体移动到球体的位置，通常的做法是先计算出二者的方向，也就是从V1指向V2的向量，计算公式是Vector3 dir = (V2V1).normalized，公式的含义是将两个向量相减并且单位化，normalized表示向量单位化，这是使用Unity自带的接口实现的，方向是没有大小的。假设V1表示的物体为obj的位置，那么它当前的位置表示为obj.transform.position，它移动到V2的位置，用Unity的计算公式表示为obj.transform.position=obj.transform.position+dir*0.5（系数）。系数的大小是可以任意设置的，要根据效果表现设置系数大小。读者可能比较熟悉这个公式，它的原型正是直线方程y=ax+b，在不知不觉中我们把数学运算公式就用上了，所以编程还是非常有趣的，接下来再看看向量的减法。

向量的减法

向量的减法在几何图上的表示如图1-8所示。

图1-8中的黑色箭头表示的是向量a和向量b。为了做减法，将向量b取反，再相加得到的是ab。向量的减法在游戏开发中主要应用在计算方向上，正如图1-7所示，一个物体从位置V1移动到位置V2，首先要做的就是确定其移动的方向，这个方向的计算公式是Vector3dir=(V2V1).normalized。除了计算方向外，计算两个物体之间的距离也是向量相减然后求平方根得到的，在Unity中可以使用函数Vector3.Distance(Vector3a，Vector3b)获取两个向量之间的距离。两个物体之间的距离的计算在游戏中运用得非常多，比如导弹要击中某个物体，需要根据导弹的射程也就是距离计算，MMOARPG游戏中玩家与怪物之间进行战斗也要判断两个物体之间的距离，从而决定是否击中对方，只有在两者相距小于某个设定的数值时，也就是在攻击范围内才能发起攻击。玩家攻击怪物的游戏效果如图1-9所示。

向量点乘

网上流传着这样一句话：向量点乘计算角度，向量叉乘计算方位。在游戏开发中通常使用点乘计算角度，点乘得到的值是个弧度常量，当然也可以将其转化成角度值。形象地说就是，当一个怪物在你身后时，叉乘可以判断你是往左转还是往右转才能更快地转向怪物，点乘得到当前面的朝向和到怪物的方向所成的角度大小。点乘向量的几何图表示如图1-10所示。

其中，|a|表示向量a的长度，|b|表示向量b的长度。θ表示向量a和向量b的角度。计算公式a×b=|a|×|b|×cosθ，也可以通过算式a×b=ax×bx+ay×by计算。

公式的几何意义是：向量a在向量b上的投影。为了让读者更好地理解，形象的表示为一个手电筒照射两个向量，可以看到光束照射的位置就是向量的投影，如图1-11所示。

还有一个问题，为什么是cosθ，看图1-12就会立刻明白了，在使用向量点乘时，必须确保向量是有意义的。

图1-12　向量点乘的计算表示

上面讲述的都是在2D空间上的向量点乘，在Unity游戏开发中可以直接调用Unity提供的库函数Vector2.Dot（Vector2a，Vector2b），返回值是一个float型的数值。接下来介绍向量在3D空间的表示，如图1-13所示。

计算方法跟2D空间是一样的，只是3D空间多了一个z轴。当然，在Unity3D开发中计算点乘不用这么复杂，可以直接使用Unity提供的库函数Vector3.Dot（Vector3a，Vector3b）。之所以介绍这么多也是为了让开发者更容易理解向量的点乘计算。在游戏中，比如玩家转向NPC（非玩家角色）、玩家转向怪物等都与向量的点乘相关，它的游戏效果如图1-14所示。

1.2.4　向量叉乘
两个向量叉乘得到的是一个向量，这个向量主要用于表示两个向量的位置关系，比如一个物体是在另一个物体的哪个方位？是前方、后方，还是左方、右方？向量叉乘表示如图1-15所示。

向量叉乘的计算公式是a×b=|a||b|sinθ。其中|a|表示a的长度值，|b|表示b的长度值。θ表示两个向量之间的夹角，a×b得到的是一个垂直于向量a和向量b的向量。在Unity3D空间的表示如图1-16所示。

图1-15　向量叉乘表示

图1-16　向量叉乘计算

假定向量a和向量b始于原点（0，0，0），那么的计算公式如下所示。

通过上面的公式可求出ab的值，以上是理论阐述。在Unity中可以直接调用引擎提供的接口Vector3.Cross（Vector3a，Vector3b）得到值类型是Vector3，也就是垂直于向量a和b的向量。向量叉乘如何在游戏中运用，在一个平面内的两个非平行向量叉乘的结果是这个平面的法向量，这个法向量是有方向的，它的方向可以用“右手定则”来判断。具体的判断方法是：若坐标系是满足右手定则的，当右手的四指从向量a以不超过180°的转角转向向量b时，竖起的大拇指的指向是向量n的方向，也就是上图中的a×b的方向。在右手坐标系中，当向量a和向量b作叉乘运算时，利用“右手定则”可以知道：当法向量n与某一坐标轴同向时，四指方向为逆时针方向；当法向量n与该坐标轴反向时，四指方向为顺时针方向。同时“右手定则”要求转角不超过180°的方向，所以用叉乘判断的转向一定是最优转向（所要转动的角度最小，转动的代价也就最小）。在游戏中可利用这点来判断一个角色是顺时针转动还是逆时针转动才能更快地转向一个敌人，而点乘计算得到的是角度，与叉乘还是有区别的。下面再举个例子给读者讲解一下，如图1-17所示的方向盘转向。

图1-17　方向盘转向

为了便于学习，先把代码给大家展示一下：

void RotateWheel (Vector3 pos)
{
    currVec = pos - wheelPos;//计算方向盘中心点到触控点的向量

    Vector3 normalVec = Vector3.Cross(currVec, oldVec);//计算法向量
    float vecAngle = Vector2.Angle(currVec, oldVec);//计算两个向量的夹角

    //使用“右手定则”可知，当大拇指方向指向我们时，四指方向为逆时针方向
    //当大拇指方向远离我们时，四指方向为顺时针方向
    //这里叉乘后的法向量平行于z轴，所以用法向量的z分量的正负判断法向量方向
    if (normalVec.z > 0)//和z轴同向，则顺时针转
    {
        wheelObj.transform.Rotate(Vector3.forward, -vecAngle);//顺时针转
    }
    else if (normalVec.z < 0)//和z轴反向，则逆时针转
    {
        wheelObj.transform.Rotate(Vector3.forward, vecAngle);//逆时针转
    }

    oldVec = currVec;//赋值
}

在赛车游戏中通常会用方向盘，以上代码就是运用向量叉乘判断一个方向盘的转向问题，希望读者能够真正掌握向量的基本运算。这些都是最基础的知识，关于向量的运算就给大家介绍到这里，下面开始介绍矩阵运算。

矩阵

向量和矩阵是线性代数非常重要的组成部分，3D引擎底层对于矩阵的使用非常多，比如局部坐标到世界坐标的转化、世界坐标到投影坐标的转化等。它们之间的转化是通过与矩阵相乘得到的，这里面就涉及3D固定流水线。作为3D游戏开发者，必须要知道两个流水线：一个是固定流水线，另一个是可编程流水线。下面简单介绍一下二者。先说固定流水线，简单地说就是一个3D物体在显示器上成像的过程，读者可能会有疑问，这与矩阵有什么关系呢？先给大家看一下固定流水线，如图1-18所示。

图1-18　固定流水线

下面介绍一下如何将物体从最初的局部坐标经过一系列矩阵变换转换到另一个坐标系，转换矩阵中最重要的是模型矩阵、视图矩阵、投影矩阵这三个矩阵。首先，顶点坐标开始于局部空间也称为局部坐标，然后经过世界坐标、观察坐标、裁剪坐标，最后以屏幕坐标结束，这些变换最终目的是将物体在屏幕上展现出来，整个流程如图1-19所示。

图1-19　矩阵变换

如果大家还感觉迷惑，我把图1-19再给大家详细解释一遍，为了让读者更好地领会它的含义，我将其总结成以下五点：

局部坐标是对象相对于局部原点的坐标，也是对象开始的坐标。
将局部坐标转换为世界坐标，世界坐标是作为一个更大空间范围的坐标系。这些坐标是相对于世界原点的。
接下来我们将世界坐标转换为观察坐标，观察坐标是指以摄像机或观察者的角度观察的坐标。
在将坐标处理到观察坐标之后，我们需要将其投影到裁剪坐标上。裁剪坐标是在1.0到1.0范围内判断哪些顶点将会出现在屏幕上的。
最后，我们需要将裁剪坐标转换为屏幕坐标，我们将这一过程称为视口变换（Viewport Transform）。视口变换将位于1.0到1.0范围内的坐标转换到由视口函数所定义的坐标范围内。转换的坐标将会送到光栅器中，由光栅器将其转化为片段。
在这里结合案例给大家描述一下，将上述思想运用到游戏开发中。比如用Unity编辑器搭建一个游戏场景，首先请美工用MAX工具建好需要的模型并将其导成fbx文件格式。建好的模型其实就是一个简单的个体，也就是个体的坐标，即局部坐标，从MAX导出模型时要将其模型位置重置成（0，0，0），然后将其拖放到Unity编辑器里面。在默认情况下，它是与世界坐标系位置重合在世界坐标的（0，0，0）位置上的。因为物体不能都堆放在世界中心点（0，0，0）的位置上，需要拖动将其摆放在编辑器的不同位置上，拖放的过程就是在Unity引擎内部实现一个把模型从局部坐标到世界坐标的变换，这个变换其实就是模型的点与世界矩阵相乘转化到世界坐标上的过程。接下来要在程序中看到这个场景，就需要放置一个虚拟摄像机，将物体放到摄像机里面，这个过程就是把物体从世界坐标转换到观察坐标，这中间是与摄像机矩阵相乘得到的，当然后面就要做消隐，也就是背面消除，因为只能看到物体的正面，背面是看不到的，这也是程序中为了优化效率考虑的，背面不需要绘制。为了使场景明亮，需要打上灯光，场景点亮之后，就可以通过虚拟摄像机来观察虚拟世界了，虚拟摄像机其实跟现实生活中人的眼睛一样。人眼有观察距离，眼睛两侧的物体是看不到的，在虚拟世界中也是一样的，看不到的物体我们就可以将其裁减掉，这里面就涉及观察坐标到透视坐标的转换，为了方便计算将物体做投影计算。为了在显示屏幕上看到，我们将其转化到视口坐标上。最后就是光栅化。这样整个固定流水线就完成了，这中间涉及的变换都与矩阵有关。

再介绍一下可编程流水线。随着硬件的发展，显卡的运算能力得到了很大提升，这也就是通常说的GPU编程。在显卡不发达时，绘制3D物体都是通过固定流水线实现的，随着显卡的提高，就出现了可编程流水线，可编程流水线其实就是把CPU上进行的运算搬到显卡的GPU中运算。也就是说，将矩阵之间的换算放到GPU中计算，这样就可以把CPU解放出来。关于可编程流水线，我会在第14章给大家详细介绍。

矩阵的运算包括矩阵加法、矩阵减法、矩阵乘法等，在游戏开发中使用最多的还是矩阵乘法，本书的编写以实用为主，因此主要介绍矩阵乘法。上面介绍了固定流水线和可编程流水线，矩阵的运用远远不止这些。下面就介绍一下矩阵在Unity编辑器中的使用，在讲解的过程中同时给大家展现一下Unity引擎内部是如何处理的。

平移矩阵

在3D空间中，把一个对象从一个位置移到另一个位置，在引擎底层进行了平移矩阵的换算，下面给大家具体讲一下，如图1-20所示。

图1-20 3D空间位置平移

在3D空间中，把对象从P点移动到P’点，运用数学公式，可以计算出二者的转换关系，如下所示。

以上是多项式，根据这个多项式可以将它们换算成一个通用的并且可以使用矩阵表示的公式，如下所示。

细心的读者可能会发现一个问题，在3D空间中，点都是三维的，为什么上面矩阵换算公式是四维的？这涉及齐次坐标的概念，在这里先给大家简单介绍一下。在进行矩阵计算时，需要将三维的点转化成齐次坐标，也就是转化成4D进行计算，因为如果不转换，矩阵的线性变换是很难实现的，比如物体的平移变换、缩放变换等三维矩阵是无法完成的，这个大家可以自己测试一下。

向量和点都是三维的，那怎样区分二者呢？如果使用的是点，那就在点的最后再加一项1，齐次坐标就表示为（x，y，z，1）。如果使用的是向量，那就在向量的最后加一项0，齐次坐标就表示为（x，y，z，0）。但是向量是不可以通过矩阵换算的，点是可以的，所以以上公式表示的都是对三维的点进行换算的。在使用Unity编辑器时，通常会把物体从一个位置移动到另一个位置。由于Unity提供了非常简单的操作方式，初学者只要在编辑器中拖拉一下物体就可以变换位置，也可以单击放大缩小按钮对物体进行缩放操作。在Unity中的操作方式如图1-21所示，此图为将一个白色的物体放到Unity编辑器里面拖放。下面介绍矩阵的另一个运算——缩放。

图1-21　物体位移示意图

矩阵缩放

在3D游戏中，经常需要对物体进行缩放变换，先从理论上介绍一下如何缩放，再通过Unity给大家介绍一下。物体的缩放和平移类似，也需要缩放矩阵，如图1-22所示。

图1-22　3D物体缩放示意图

在3D空间中对于物体的缩放并不是凭空产生的，它也是经过运算得到的。运算公式如下所示。

上述公式可以写成矩阵换算，如下所示。

在Unity编辑器的实际操作过程中，引擎为开发者提供了非常便利的接口，只需要在编辑器里面简单操作就可以达到缩放的效果。它实际运行的是调用引擎内部的缩放变换矩阵，也就是用上面的矩阵公式表示的，在Unity中缩放效果如图1-23所示。

两个机器人彼此之间是经过缩放变换大小的，它就是引擎内部通过矩阵缩放实现的，类似的还有矩阵旋转。

图1-23　Unity编辑器中缩放效果

矩阵旋转

在3D游戏开发中，游戏中的3D物体旋转可以通过矩阵旋转、四元数旋转、欧拉角旋转得到。在本节中主要介绍矩阵旋转，矩阵旋转最基本的是绕x、y、z轴旋转。矩阵旋转在引擎中使用得比较多，编程时一般采用四元数或者欧拉角实现。下面分别介绍绕x、y、z轴旋转矩阵。绕x轴旋转如图1-24所示。

在这里我直接给出旋转结果矩阵，如下所示。

接下来绕y轴旋转，如图1-25所示。

图1-24　绕x轴旋转

图1-25　绕y轴旋转

绕y轴旋转矩阵如下所示。

绕z轴旋转如图1-26所示。

图1-26　绕z轴旋转

对应绕z轴旋转矩阵如下所示。

以上是矩阵在3D游戏中的计算方式，Unity引擎已经为开发者提供了旋转接口，函数transform.Rotate（newVector3（0，1，0））表示绕y轴旋转，在Rotate函数中使用了向量，它们的参数分别表示x、y、z，上述算式中y的值为1表示的是绕y轴旋转，如果是x轴为1表示的是绕x轴旋转，依此类推。接下来将其在Unity编辑器中的表现给大家展示一下，如图1-27所示。

图1-27　绕x、y、z轴旋转效果图

从右到左依次是正常摆放的角色、绕x轴旋转的角色、绕y轴旋转的角色、绕z轴旋转的角色。虽然通过工具可以很容易地将其旋转，其实在引擎内部是进行了上面列出的关于旋转矩阵的乘法计算。

物体也可以绕x、y、z轴旋转或者x、y轴旋转，它的计算方式就是绕x、y、z轴的矩阵一起相乘，当然Unity也已经为开发者封装好了，开发者只负责使用即可。为什么不厌其烦地介绍这些知识，主要目的是告诉开发者原理，这样更有助开发者编写逻辑。接下来介绍一下四元数。

四元数

首先介绍一下什么是四元数，四元数本质上是个高阶复数，表达式为y=a+bi+cj+dk。在讲矩阵时提到了旋转，四元数在Unity里面主要也是用于旋转的，在Unity编辑器里面有个Transform组件，它包括位置（Position）、旋转（Rotation）和缩放（Scale）。Rotation就是一个四元数，但是不能直接对Quaterian.Rotation赋值。可以使用函数Quaterian.Eular（Vector3angle）获取四元数，该函数返回的就是四元数。

欧拉角表示为Quaternion.eulerAngles，欧拉角可以对其进行赋值，赋值表示如下所示。

Quaternion.eulerAngles = new Vector3(0, 30, 0);
四元数可以用来进行旋转，它的表达式是Quaternion.AngleAxis（float angle，Vector3axis），调用这个函数可以对物体进行旋转，当然还需要调用函数Quaternion.Lerp（）在旋转时进行插值运算，这些函数都是在编写逻辑时调用的。四元数是不可以直接被赋值的，四元数推理比较麻烦，读者如果想了解可以自己在网上查阅资料，本节的主要目的是告诉读者用四元数解决问题，接下来说一下欧拉角。

欧拉角

欧拉角也是用于旋转的，只是它有一个致命的缺点，就是万向节死锁，欧拉角旋转我们在Unity开发中通常使用的函数是transform.Rotate（Vector3angle）。

现在介绍一下万向节死锁，其实就是在3D空间中某两个轴在旋转时重叠了，不论你如何旋转，三个轴就变成了两个轴，给大家举个会出现万向节死锁的例子：

transform.Rotate(new Vector3(0, 0, 40));
transform.Rotate(new Vector3(0, 90, 0));
transform.Rotate(new Vector3(80, 0, 0));
我们只需要固定中间一句代码，即使y轴的旋转角度始终为90°，那么你会发现无论怎么调整x轴和z轴的旋转角度，它们会像一个钟表的表针一样总是在同一个平面上运动。

万向节锁中的“锁”，其实是给人一种误导，这可能也是让很多人觉得难以理解的一个原因。实际上，它并没有锁住任何一个旋转轴，只是在这种旋转情况下我们会感觉丧失了一个维度。以上面的例子来说，尽管固定了第二个旋转轴的角度为90°，但我们原以为依靠改变其他两个轴的旋转角度是可以得到任意旋转位置的（因为按我们的理解，两个轴应该控制的是两个空间维度），而事实是它被“锁”在了一个平面上，即只有一个维度了，缺失了一个维度。而只要第二个旋转轴不是±90°，我们就可以依靠改变其他两个轴的旋转角度来得到任意旋转位置。

从最简单的矩阵来理解，还是使用x、y、z的旋转顺序。当y轴的旋转角度为90°时，我们会得到下面的旋转矩阵。

我们对上述矩阵进行左乘可以得到下面的结果：

当我们改变第一次和第三次的旋转角度时，是同样的效果，而不会改变第一行和第三列的任何数值，从而缺失了一个维度。我们再尝试着理解下它的本质，万向节锁出现的本质原因，是因为从欧拉角到旋转的映射并不是一个覆盖映射，即它并不是在每个点处都是局部同胚的。通俗地解释一下，这意味着从欧拉角到旋转是一个多对一的映射（即不同的欧拉角可以表示同一个旋转方向），而且并不是每一个旋转变化都可以用欧拉角来表示。

小结

数学的基础知识已经给大家讲完了，这些最基本的数学知识开发者要熟练掌握。对于图形学的一些高级算法大家有兴趣可以学习一下，用得比较多的是贝济埃曲线、B样条曲线等，二者都可以应用到刀光拖尾算法、曲线插值算法中。在Unity中有iTween曲线插件和DotTween曲线插件等，下面开始讲解开发3DMMORPG游戏经常使用的Avatar换装开发技术。