思考并回答以下问题：

贪心算法的定义是什么？
利用贪心算法求解的问题往往具有两个重要的特性：贪心选择性质和最优子结构性质。这两个是什么意思？
冒泡排序使用了贪心算法。怎么理解？

本章涵盖：

贪心算法
最优装载问题
背包问题
会议安排
最短路径
哈夫曼编码
最小生成树

贪心算法

贪心本质

1	一个贪心算法总是做出当前最好的选择，也就是说，它期望通过局部最优选择从而得到全局最优的解决方案。 --《算法导论》

贪心算法从问题的初始解开始，一步一步地做出当前最好的选择，逐步逼近问题的目标，尽可能地得到最优解，即使达不到最优解，也可以得到最优解的近似解。

贪心算法在解决问题的策略上“目光短浅”，只根据当前已有的信息就做出选择，而且一旦做出了选择，不管将来有什么结果，这个选择都不会改变。换言之，贪心算法并不是从整体最优考虑，它所做出的选择只是在某种意义上的局部最优。贪心算法能得到许多问题的整体最优解或整体最优解的近似解。因此，贪心算法在实际中得到大量的应用。

在贪心算法中，我们需要注意以下几个问题。

（1）没有后悔药。一旦做出选择，不可以反悔。
（2）有可能得到的不是最优解，而是最优解的近似解。
（3）选择什么样的贪心策略，直接决定算法的好坏。

那么，贪心算法需要遵循什么样的原则呢？

贪亦有道

通常我们在遇到具体问题时，往往分不清哪些问题该用贪心策略求解，哪些问题不能使用贪心策略。经过实践我们发现，利用贪心算法求解的问题往往具有两个重要的特性：贪心选择性质和最优子结构性质。如果满足这两个性质就可以使用贪心算法了。

（1）贪心选择

所谓贪心选择性质是指原问题的整体最优解可以通过一系列局部最优的选择得到。应用同一规则，将原问题变为一个相似的但规模更小的子问题，而后的每一步都是当前最佳的选择。这种选择依赖于已做出的选择，但不依赖于未做出的选择。运用贪心策略解决的问题在程序的运行过程中无回溯过程。关于贪心选择性质，读者可在后续的贪心策略状态空间图中得到深刻的体会。

（2）最优子结构

当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。问题的最优子结构性质是该问题是否可用贪心算法求解的关键。例如原问题S={a₁, a₂ , …, a_i, …, a_n}，通过贪心选择选出一个当前最优解{a_i}之后，转化为求解子问题S-{a_i}，如果原问题的最优解包含子问题的最优解，则说明该问题满足最优子结构性质，如图2-1所示。

图2-1 原问题和子问题

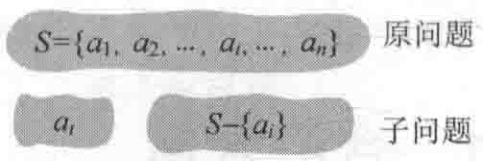
贪心算法秘籍

上面我们已经知道了具有贪心选择和最优子结构性质就可以使用贪心算法，那么如何使用呢？下面介绍贪心算法秘籍。

（1）贪心策略

首先要确定贪心策略，选择当前看上去最好的一个方案。例如，挑选苹果，如果你认为个大的是最好的，那你每次都从苹果堆中拿一个最大的，作为局部最优解，贪心策略就是选择当前最大的苹果；如果你认为最红的苹果是最好的，那你每次都从苹果堆中拿一个最红的，贪心策略就是选择当前最红的苹果。因此根据求解目标不同，贪心策略也会不同。

（2）局部最优解

根据贪心策略，一步一步地得到局部最优解。例如，第一次选一个最大的苹果放起来，记为a₁，第二次再从剩下的苹果堆中选择一个最大的苹果放起来，记为a₂，以此类推。

（3）全局最优解

把所有的局部最优解合成为原来问题的一个最优解（a₁, a₂, …）。

1	怎么有点儿像冒泡排序啊？

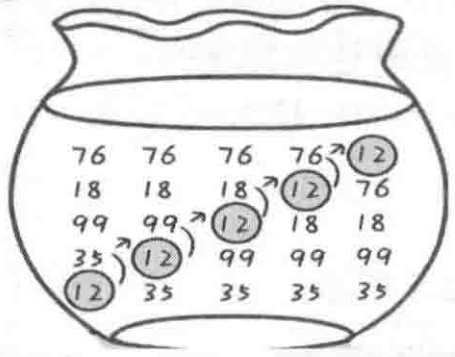
不是贪心算法像冒泡排序，而是冒泡排序使用了贪心算法，它的贪心策略就是每一次从剩下的序列中选一个最大的数，把这些选出来的数放在一起，就得到了从大到小的排序结果，如图2-2所示。

图2-2 冒泡排序

最优装载问题

海盗们截获了一艘裝滿各种各样古董的货船，每一件古董都价值连城，一旦打碎就失去了它的价值。虽然海盗船足够大，但载重量为C，每件古董的重量为w_i，海盗们该如何把尽可能多数量的宝贝装上海盗船呢？

问题分析

根据问题描述可知这是一个可以用贪心算法求解的最优装载问题，要求装载的物品的数量尽可能多，而船的容量是固定的，那么优先把重量小的物品放进去，在容量固定的情况下，装的物品最多。采用重量最轻者先装的贪心选择策略，从局部最优达到全局最优，从而产生最优装载问题的最优解。

算法设计

（1）当载重量为定值c时，w_i越小时，可装载的古董数量n越大。只要依次选择最小重量古董，直到不能再装为止。
（2）把n个古董的重量从小到大（非递减）排序，然后根据贪心策略尽可能多地选出前i个古董，直到不能继续装为止，此时达到最优。

完美图解

每个古董的重量如表2-1所示，海盗船的载重量c为30，那么在不能打碎古董又不超过载重的情况下，怎么装入最多的古董？

表2-1 古董重量清单

（1）因为贪心策略是每次选择重量最小的古董装入海盗船，因此可以按照古董重量非递减排序，排序后如表2-2所示。

表2-2 按重量排序后古董清单

（2）按照贪心策略，每次选择重量最小的古董放入（tmp代表古董的重量，ans代表已装裁的古董个数）。

i=0，选择排序后的第1个，装入重量tmp=2，不超过载重量30，ans=1。
i=l，选择排序后的第2个，装入重量tmp=2+3=5，不超过载重量30，ans=2。
i=2，选择排序后的第3个，装入重量tmp=5+4=9，不超过载重量30，ans=3。
i=3，选择排序后的第4个，装入重量tmp=9+5=14，不超过载重量30，ans=4。
i=4，选择排序后的第5个，装入重量tmp=14+7=21，不超过载重量30，ans=5。
i=5，选择排序后的第6个，装入重量tmp=21+10=31，超过载重量30，算法结束。

即放入古董的个数为ans=5个。

伪代码详解

（1）数据结构定义

根据算法设计描述，我们用一维数组存储古董的重量：

1	double w[N]; // 一维数组存储古董的重量

（2）按重量排序

可以利用C++中的排序函数sort，对古董的重量进行从小到大（非递减）排序。要使用此函数需引入头文件：

1	#include <algorithm>

语法描述为:

1	sort(begin, end) // 参数begin和end表示一个范围，分别为待排序数组的首地址和尾地址 sort函数默认为升序

在本例中只需要调用sort函数对古董的重量进行从小到大排序：

1	sort(w, w+n); // 按古董重量升序排序

（3）按照贪心策略找最优解

首先用变量ans记录已经装载的古董个数，tmp代表装载到船上的古董的重量，两个变量都初始化为0。然后按照重量从小到大排序，依次检查每个古董，tmp加上该古董的重量，如果小于等于载重量c，则令ans++；否则，退出。

int tmp = 0, ans = 0; // tmp代表装载到船上的古董的重量，ans记录已经装载的古董个数
for （int i= 0; i < n; i++）
{
    tmp += w[i];
    if(tmp <= c)
        ans ++;
    else
        break;
}

实战演练

// program 2-1
#include <iostream>
#include <algorithm>

const int N = 1000005;
using namespace std;

double w[N]; // 古董的重量数组

int main()
{
    double c;
    int n;
    cout<<"请输入古董重量c及古董个数n: "<<endl;
    cin>>c>>n;
}

算法解析及优化拓展

1.算法复杂度分析

（1）时间复杂度：首先需要按古董重量排序，调用sort函数，其平均时间复杂度为O(nlogn)，输入和贪心策略求解的两个for语句时间复杂度均为O(n)，因此时间复杂度为O(n+ nlog(n))。
（2）空间复杂度：程序中变量tmp、ans等占用了一些辅助空间，这些辅助空间都是常数阶的，因此空间复杂度为O(1)。

2.优化拓展

（1）这一个问题为什么在没有装满的情况下，仍然是最优解？算法要求装入最多数量，假如c为5，4个物品重量分别为1、3、5、7，排序后，可以装入1和3，最多装入两个。分析发现是最优的，如果装大的物品，最多装一个或者装不下，所以选最小的先装才能装入最多的数量，得到解是最优的。

（2）在伪代码详解的第3步“按照贪心策略找最优解”，如果把代码替换成下面代码，有什么不同？

首先用变量ans记录已经装载的古董个数，初始化为n；tmp代表装载到船上的古董的重量，初始化为0。然后按照重量从小到大排序，依次检查每个古董，tmp加上该古董的重量，如果tmp大于等于载重量c，则判断是否正好等于载重量c，并令ans=i+1；否则ans=i，退出。如果tmp小于载重量c，i++，继续下一个循环。

1
2

（3）如果想知道装入了哪些古董，需要添加什么程序来实现呢？请大家动手试一试吧！

那么，还有没有更好的算法来解决这个问题呢？

背包问题

问题分析

假设山洞中有n种宝物，每种宝物有一定重量w和相应的价值v，毛驴运载能力有限，只能运走m重量的宝物，一种宝物只能拿一样，宝物可以分割。那么怎么才能使毛驴运走宝物的价值最大呢？

我们可以尝试贪心策略：

（1）每次挑选价值最大的宝物装入背包，得到的结果是否最优？
（2）每次挑选重量最小的宝物装入，能否得到最优解？
（3）每次选取单位重量价值最大的宝物，能否使价值最高？

思考一下，如果选价值最大的宝物，但重量非常大，也是不行的，因为运载能力是有限的，所以第1种策略含弃；如果选重量最小的物品装入，那么其价值不一定高，所以不能在总重限制的情况下保证价值最大，第2种策略舍弃；而第3种是每次选取单位重量价值最大的宝物，也就是说每次选择性价比（价值/重量）最高的宝物，如果可以达到运载重量m，那么一定能得到价值最大。

因此采用第3种贪心策略，每次从剩下的宝物中选择性价比最高的宝物。

算法设计

（1）数据结构及初始化。将n种宝物的重量和价值存储在结构体three （包含重量、价值、性价比3个成员）中，同时求出每种宝物的性价比也存储在对应的结构体three中，将其按照性价比从高到低排序。采用sum来存储毛驴能够运走的最大价值，初始化为0.
（2）根据贪心策略，按照性价比从大到小选取宝物，直到达到毛驴的运载能力。每次选择性价比高的物品，判断是否小于m（毛驴运载能力），如果小于m，则放入， sum（已放入物品的价值）加上当前宝物的价值，m减去放入宝物的重量；如果不小于m，则取该宝物的一部分m * p[i]，m=0，程序结束。m减少到0，则sum得到最大值。

完美图解

假设现在有一批宝物，价值和重量如表2-3所示，毛驴运载能力m=30，那么怎么装入最大价值的物品？

表2-3 宝物清单

（1）因为贪心策略是每次选择性价比（价值/重量）高的宝物，可以按照性价比降序排序，排序后如表2-4所示。

表2-4 排序后宝物清单

（2）按照贪心策略，每次选择性价比高的宝物放入：

第1次选择宝物2，剩余容量30-2=28，目前装入最大价值为8。
第2次选择宝物10，剩余容量28-5=23，目前装入最大价值为8+15=23。
第3次选择宝物6，剩余容量23-8=15，目前装入最大价值为23+20=43。
第4次选择宝物3，剩余容量15-9=6，目前装入最大价值为43+18=61。
第5次选择宝物5，剩余容量6-5=1，目前装入最大价值为61+8=69。
第6次选择宝物8，发现上次处理完时剩余容量为1，而8号宝物重量为4，无法全部放入，那么可以采用部分装入的形式，装入1个重量单位，因为8号宝物的单位重量价值为1.5，因此放入价值1x1.5=1.5，你也可以认为装入了8号宝物的1/4，目前装入最大价值为69+1.5=70.5，剩余容量为0。

（3）构造最优解

把这些放入的宝物序号组合在一起，就得到了最优解（2, 10, 6, 3, 8），其中最后一个宝物为部分装入（装了8号财宝的1/4），能够装入宝物的最大价值为70.5。

伪代码详解

（1）数据结构定义

根据算法设计中的数据结构，我们首先定义一个结构体three：

struct three
{
    double w; // 每种宝物的重量
    double v; // 每种宝物的价值
    double p; // 每种宝物的性价比（价值/重量）
}

（2）性价比排序

我们可以利用C++中的排序函数sort，对宝物的性价比从大到小（非递增）排序。要使用此函数需引入头文件：

1	#include <algorithm>

语法描述为：

1	sort(begin, end) // 参数begin和end表示一个范围，分别为待排序数组的首地址和尾地址

在本例中我们采用结构体形式存储，按结构体中的一个字段，即按性价比排序。如果不使用自定义比较函数，那么sort函数排序时不知道按哪一项的值排序，因此采用自定义比较函数的办法实现宝物性价比的降序排序：

bool cmp (three a, three b) // 比较函数按照宝物性价比降序排列
{
    return a.p > b.p; // 指明按照宝物性价比降序排列
}

sort(s, s+n, cmp) ; //前两个参数分别为待排序数组的首地址和尾地址 最后一个参数compare表示比较的类型

（3）贪心算法求解

在性价比排序的基础上，进行贪心算法运算。如果剩余容量比当前宝物的重量大，则可以放入，剩余容量减去当前宝物的重量，已放入物品的价值加上当前宝物的价值。如果剩余容量比当前宝物的重量小，表示不可以全部放入，可以切割下来一部分（正好是剩余容量），然后令剩余容量乘以当前物品的单位重量价值，已放入物品的价值加上该价值，即为能放入宝物的最大价值。

for (int i = 0;i < n; i++)// 按照排好的顺序，执行贪心策略
{
    if( m > s[i].w ) // 如果宝物的重量小于毛驴剩下的运载能力，即剩余容量
    {
        m -= s[i].w;
        sum += s[i].v;
    }
    else // 如果宝物的重量大于毛驴剩下的承载能力
    {
        sum += m乘以s[i].p; // 进行宝物切割，切割一部分（m重量），正好达到驴子承重
        break;
    }
}

实战演练

1
2

算法解析及优化拓展

1.算法复杂度分析

（1）时间复杂度：该算法的时间主要耗费在将宝物按照性价比排序上，采用的是快速排序，算法时间复杂度为O(nlogn)。

（2）空间复杂度：空间主要耗费在存储宝物的性价比，空间复杂度为0(n)。

为了使m重量里的所有物品的价值最大，利用贪心思想，每次取剩下物品里面性价比最高的物品，这样可以使得在相同重量条件下比选其他物品所得到的价值更大，因此采用贪心策略能得到最优解。

2.算法优化拓展

那么想一想，如果宝物不可分割，贪心算法是否能得到最优解？

下面我们看一个简单的例子。

假定物品的重量和价值已知，如表2-5所示，最大运载能力为10。采用贪心算法会得到怎样的结果？

表2-5 物品清单

如果我们采用贪心算法，先装性价比高的物品，且物品不能分割，剩余容量如果无法再装入剩余的物品，不管还有没有运载能力，算法都会结束。那么我们选择的物品为1和2，总价值为31，而实际上还有3个剩余容量，但不足以装下剩余其他物品，因此得到的最大价值为31。但实际上我们如果选择物品2和3，正好达到运载能力，得到的最大价值为34。也就是说，在物品不可分割、没法装满的情况下，贪心算法并不能得到最优解，仅仅是最优解的近似解。

想一想，为什么会这样呢？

物品可分割的装载问题我们称为背包问题，物品不可分割的装载问题我们称之为0-1背包问题。

在物品不可分割的情况下，即0-1背包问题，已经不具有贪心选择性质，原问题的整体最优解无法通过一系列局部最优的选择得到，因此这类问题得到的是近似解。如果一个问题不要求得到最优解，而只需要一个最优解的近似解，则不管该问题有没有贪心选择性质都可以使用贪心算法。

想一想，上一节中加勒比海盗船问题为什么在没有装满的情况下，仍然是最优解，而0-1背包问题在没装满的情况下有可能只是最优解的近似解？

会议安排

某跨国公司总裁正分身无术，为一大堆会议时间表焦头烂额，希望秘书能做出合理的安排，能在有限的时间内召开更多的会议。

问题分析

这是一个典型的会议安排问题，会议安排的目的是能在有限的时间内召开更多的会议（任何两个会议不能同时进行）。在会议安排中，每个会议i都有起始时间bi和结束时间ei，且bi < ei，即一个会议进行的时间为半开区间[bi, ei），如果[bi, ei）与[bj, ej）均在“有限的时间内”，且不相交，则称会议i与会议j相容的。也就是说，当b>e，或b，e时，会议i与会议j相容。会议安排问题要求在所给的会议集合中选出最大的相容活动子集，即尽可能在有限的时间内召开更多的会议。

在这个问题中，“有限的时间内（这段时间应该是连续的）”是其中的一个限制条件，也应该是有一个起始时间和一个结束时间（简单化，起始时间可以是会议最早开始的时间，结束时间可以是会议最晚结束的时间），任务就是实现召开更多的满足在这个“有限的时间内”等待安排的会议，会议时间表如表2-6所示。

表2-6

会议安排的时间段如图2-7所示。

从图2-7中可以看出，（会议1，会议4，会议6，会议8，会议9），（会议2，会议4，会议7，会议8，会议9）都是能安排最多的会议集合。要让会议数最多，我们需要选择最多的不相交时间段。我们可以尝试贪心策略:

图2-7 会议安排时间段

（1）每次从剩下未安排的会议中选择会议具有最早开始时间且与已安排的会议相容的会议安排，以增大时间资源的利用率。

（2）每次从剩下未安排的会议中选择持续时间最短且与已安排的会议相容的会议安排，这样可以安排更多一些的会议。

（3）每次从剩下未安排的会议中选择具有最早结束时间且与已安排的会议相容的会议安排，这样可以尽快安排下一个会议。

思考一下，如果选择最早开始时间，则如果会议持续时间很长，例如8点开始，却要持续12个小时，这样一天就只能安排一个会议;如果选择持续时间最短，则可能开始时间很晚，例如19点开始，20点结束，这样也只能安排一个会议，所以我们最好选择那些开始时间要早，而且持续时间短的会议，即最早开始时间+持续时间最短，就是最早结束时间。

因此采用第（3）种贪心策略，每次从剩下的会议中选择具有最早结束时间且与已安排的会议相容的会议安排。

算法设计

（1）初始化:将n个会议的开始时间、结束时间存放在结构体数组中（想一想，为什么不用两个一维数组分别存储？），如果需要知道选中了哪些会议，还需要在结构体中增加会议编号，然后按结束时间从小到大排序（非递减），结束时间相等时，按开始时间从大到小排序（非递增）；

（2）根据贪心策略就是选择第一个具有最早结束时间的会议，用last记录刚选中会议的结束时间；

（3）选择第一个会议之后，依次从剩下未安排的会议中选择，如果会议1开始时间大于等于最后一个选中的会议的结束时间last，那么会议，与已选中的会议相容，可以安排，更新last为刚选中会议的结束时间;否则，舍弃会议i，检查下一个会议是否可以安排。

完美图解

1，原始的会议时间表（见表2-7）:

表2-7 原始会议时间表

2.排序后的会议时间表（见表2-8）:

表2-8 排序后的会议时间表

3.贪心选择过程

（1）首先选择排序后的第一个会议即最早结束的会议（编号为2），用last记录最后一个被选中会议的结束时间， last-4.

（2）检查余下的会议，找到第一个开始时间大于等于last （last-4）的会议，子问题转化为从该会议开始，余下的所有会议。如表2-9所示。

表2-9

选项	作用

会议num开始时间bog结束时间end
会议时间表

从子问题中，选择第一个会议即最早结束的会议（编号为3），更新last为刚选中会议的结束时间last7.（3）检查余下的会议，找到第一个开始时间大于等于last （last-7）的会议，子问题转化为从该会议开始，余下的所有会议。如表2-10所示。表2-10 会议时间表会inum开始时间beg结束时间end

从子问题中，选择第一个会议即最早结束的会议（编号为7），更新last为刚选中会议的结束时间last-111

（4）检查余下的会议，找到第一个开始时间大于等于last （last-11）的会议，子问题转化为从该会议开始，余下的所有会议。如表2-11所示。
表2-11会议num开始时间beg结束时间end
会议时间表

从子问题中，选择第一个会议即最早结束的会议（编号为10），更新last为刚选中会议的结束时间last-14:所有会议检查完毕，算法结束。如表2-12所示。

4，构造最优解

从贪心选择的结果，可以看出，被选中的会议编号为（2， 3， 7， 10}，可以安排的会议数量最多为4，如表2-12所示。
表2-12会议num开始时间beg结束时间end
会议时间表
.4.4
伪代码详解
（1）数据结构定义
以下C+程序代码中，结构体meet中定义了beg表示会议的开始时间， end表示会议的结束时间，会议meer的数据结构:

1
2
3

struct Meet
int beg; //会议的开始时间
int end; //会议的结束时间

（2）对会议按照结束时间非递减排序
我们采用C++中自带的sort函数，自定义比较函数的办法，实现会议排序，按结束时间从小到大排序（非递减），结束时间相等时，按开始时间从大到小排序（非递增）;
使用上面贪心算法可得，选择的会议是第2、3、7，10个会议，输出最优值是4.

算法解析及优化拓展

1，算法复杂度分析

（1）时间复杂度:在该算法中，问题的规模就是会议总个数n。显然，执行次数随问题规模的增大而变化。首先在成员函数setMeet:init）中，输入n个结构体数据。输入作为基本语句，显然，共执行n次。而后在调用成员函数setMeet:solve）中进行排序，易知sort排序函数的平均时间复杂度为O（nlogn），随后进行选择会议，贡献最大的为if（meetij].beg -last）语句，时间复杂度为0（n），总时间复杂度为O（n+nlogn）-O（nlogr）.

（2）空间复杂度:在该算法中， meen]结构体数组为输入数据，不计算在空间复杂度内。辅助空间有i， n， ans等变量，则该程序空间复杂度为常数阶，即0（1）.
2.算法优化拓展
想一想，你有没有更好的办法来处理此问题，比如有更小的算法时间复杂度？

最短路径

问题分析

根据题目描述可知，这是一个求单源最短路径的问题。给定有向带权图G=（V，E），其中每条边的权是非负实数。此外，给定V中的一个顶点，称为源点。现在要计算从源到所有其他各顶点的最短路径长度，这里路径长度指路上各边的权之和。

如何求源点到其他各点的最短路径呢？

算法设计

Dijikstra算法是解决单源最短路径问题的贪心算法，它先求出长度最短的一条路径，再参照该最短路径求出长度次短的一条路径，直到求出从源点到其他各个顶点的最短路径。

Djkstra算法的基本思想是首先假定源点为u，顶点集合V被划分为两部分:集合s和v-S。初始时S中仅含有源点u，其中S中的顶点到源点的最短路径已经确定。集合以-S中所包含的顶点到源点的最短路径的长度待定，称从源点出发只经过s中的点到达r-s中的点的路径为特殊路径，并用数组dis1]记录当前每个顶点所对应的最短特殊路径长度。

Dijkstra算法采用的贪心策略是选择特殊路径长度最短的路径，将其连接的V-S中的顶点加入到集合s中，同时更新数组dis。一旦S包含了所有顶点， dis门]就是从源到所有其他顶点之间的最短路径长度。

（1）数据结构。设置地图的带权邻接矩阵为mapU，即如果从源点u到顶点i有边，就令map[u][]等于< u, i >的权值，否则map[u][i=o0（无穷大）;采用一维数组dis[]来记录从源点到i顶点的最短路径长度;采用一维数组p来记录最短路径上i顶点的前驱。
（2）初始化。令集合S-（wl，对于集合V-S中的所有顶点x，初始化dis1[]-map[u][]，如果源点u到顶点;有边相连，初始化p[-u，否则plj—1
（3）找最小。在集合v-S中依照贪心策略来寻找使得dist]具有最小值的顶点t，即dis[]-min （dis[/属于V-S集合），则顶点，就是集合v-S中距离源点u最近的顶点。
（4）加入S战队。将顶点，加入集合s中，同时更新V-s.
（5）判结束。如果集合v-S为空，算法结束，否则转（6）。
（6）借东风。在（3）中已经找到了源点到r的最短路径，那么对集合V-S中所有与顶点r相邻的顶点j，都可以借助1走捷径。如果dist/ dis（1+tmap[1，则dist）-dis（[]+map[/记录顶点j的前驱为，有pj=1，转（3）

由此，可求得从源点u到图G的其余各个顶点的最短路径及长度，也可通过数组p0逆向找到最短路径上经过的城市。

完美图解

现在我们有一个景点地图，如图2-10所示，假设从1号结点出发，求到其他各个结点的最短路径。

算法步骤如下。

（1）数据结构

设置地图的带权邻接矩阵为map110，即如果从顶点i到顶点j有边，则map[0等于的权值，否则map[1V-oo （无穷大），如图2-11所示。

贪心算法

贪心本质

贪亦有道

贪心算法秘籍

最优装载问题

问题分析

算法设计

完美图解

伪代码详解

实战演练

算法解析及优化拓展

背包问题

问题分析

算法设计

完美图解

伪代码详解

实战演练

算法解析及优化拓展

会议安排

问题分析

算法设计

完美图解

算法解析及优化拓展

最短路径

问题分析

算法设计

完美图解

哈夫曼编码

最小生成树