第2章 线性表

发表于 | 更新于 | 分类于
本文字数： 29k | 阅读时长 ≈ 26 分钟

思考并回答以下问题：

  • 线性表和单链表的区别是什么？
  • 线性表和顺序表的区别是什么？
  • 二元组是什么意思？

本章涵盖：

线性表是最简单、最基本、最常用的数据结构。线性表是线性结构的抽象（Abstract），线性结构的特点是结构中的数据元素之间存在一对一的线性关系。这种一对一的关系指的是数据元素之间的位置关系，即：

  • （1）除第一个位置的数据元素外，其它数据元素位置的前面都只有一个数据元素；
  • （2）除最后一个位置的数据元素外，其它数据元素位置的后面都只有一个元素。

也就是说，数据元素是一个接一个的排列。因此，可以把线性表想象为一种数据元素序列的数据结构。

本书在介绍各种数据结构时，先介绍数据结构的逻辑结构，包括定义、基本操作。然后介绍数据结构的存储结构，先介绍顺序存储结构，再介绍链式存储结构。

线性表的逻辑结构

线性表的定义

线性表（List）是由n（n≥0）个相同类型的数据元素构成的有限序列。对于这个定义应该注意两个概念：一是“有限”，指的是线性表中的数据元素的个数是有限的，线性表中的每一个数据元素都有自己的位置（Position）。本书不讨论数据元素个数无限的线性表。二是“相同类型”，指的是线性表中的数据元素都属于同一种类型。虽然有的线性表具有不同类型的数据元素，但本书中所讨论的线性表中的数据元素都属于同一类型。

线性表通常记为：L=(a1, a2, …, ai-1, ai, ai+1, …, an)，L是英文单词list的第1个字母。L中包含n个数据元素，下标表示数据元素在线性表中的位置。a1是线性表中第一个位置的数据元素，我们称作第一个元素。an是线性表中最后一个位置的数据元素，我们称作最后一个元素。n为线性表的表长，n=0时的线性表被称为空表（Empty List）。

线性表中的数据元素之间存在着前后次序的位置关系，将ai-1称为ai的直接前驱，将ai称为ai+1的直接后继。除a1外，其余元素只有一个直接前驱，因为a1是第一个元素，所以它没有前驱。除an外，其余元素只有一个直接后继，因为an是最后一个元素，所以它没有后继。

线性表的形式化定义为：线性表（List）简记为L，是一个二元组，

其中：

  • D是数据元素的有限集合。
  • R是数据元素之间关系的有限集合。

在实际生活中线性表的例子很多。例如，1到100的偶数就是一个线性表：

(2, 4, 6, …, 100)

表中数据元素的类型是自然数。某个办公室的职员姓名（假设每个职员的姓名都不一样）也可以用一个线性表来表示：

("zhangsan", "lisi", "wangwu", "zhaoliu", "sunqi", "huangba")

表中数据元素的类型为字符串。

在一个复杂的线性表中，一个数据元素是一个记录，由若干个数据项组成，含有大量记录的线性表又称文件（File）。例如，例子1.1中的学生信息表就是一个线性表，表中的每一行是一个记录。一个记录由学号、姓名、行政班级、性别和出生年月等数据项组成。

线性表的基本操作

在选择线性表的表示法之前，程序设计人员首先应该考虑这种表示法要支持的基本操作。从线性表的定义可知，一个线性表在长度上应该能够增长和缩短，也就是说，线性表最重要的操作应该能够在线性表的任何位置插入和删除元素。除此之外，应该可以有办法获得元素的值、读出这个值或者修改这个值。也应该可以生成和清除（或者重新初始化）线性表。

数据结构的运算是定义在逻辑结构层次上的，而运算的具体实现是建立在物理存储结构层次上的。因此，把线性表的操作作为逻辑结构的一部分，每个操作的具体实现只有在确定了线性表的存储结构之后才能完成。数据结构的基本运算不是它的全部运算，而是一些常用的基本运算，而每一个基本运算在实现时也可以根据不同的存储结构派生出一系列相关的运算来。

由于现在只考虑线性表的基本操作，所以以C#接口的形式表示线性表，接口中的方法成员表示基本操作。并且，为了使线性表对任何数据类型都适用，数据元素的类型使用泛型的类型参数。在实际创建线性表时，元素的实际类型可以用应用程序中任何方便的数据类型来代替，比如用简单的整型或者用户自定义的更复杂的类型来代替。

线性表的接口如下所示。

1
2
3
4
5
6
7
8
9
10
11
public interface IListDS<T> 
{
    int GetLength(); //求长度
    void Clear(); //清空操作
    bool IsEmpty(); //判断线性表是否为空
    void Append(T item); //附加操作
    void Insert(T item, int i); //插入操作
    T Delete(int i); //删除操作
    T GetElem(int i); //取表元
    int Locate(T value); //按值查找
}

为了和.NET框架中的接口IList相区分，在IList后面加了“DS”，“DS”表示数据结构。下面对线性表的基本操作进行说明。

1、求长度：GetLength()

初始条件：线性表存在；
操作结果：返回线性表中所有数据元素的个数。

2、清空操作：Clear()

初始条件：线性表存在且有数据元素；
操作结果：从线性表中清除所有数据元素，线性表为空。

3、判断线性表是否为空：IsEmpty()

初始条件：线性表存在；
操作结果：如果线性表为空返回true，否则返回false。

4、附加操作：Append(T item)

初始条件：线性表存在且未满；
操作结果：将值为item的新元素添加到表的末尾。

5、插入操作：Insert(T item, int i)

初始条件：线性表存在，插入位置正确()(1≤i≤n+1,n为插入前的表长)。
操作结果：在线性表的第i个位置上插入一个值为item的新元素，这样使得原序号为i,i+1,…,n的数据元素的序号变为i+1,i+2,…,n+1，插入后表长=原表长+1。

6、删除操作：Delete(int i)

初始条件：线性表存在且不为空，删除位置正确(1≤i≤n,n为删除前的表长)。
操作结果：在线性表中删除序号为i的数据元素，返回删除后的数据元素。删除后使原序号为i+1,i+2,…,n的数据元素的序号变为i,i+1,…,n-1，删除后表长=原表长-1。

7、取表元：GetElem(int i)

初始条件：线性表存在，所取数据元素位置正确（1≤i≤n，n为线性表的表长）；
操作结果：返回线性表中第i个数据元素。

8、按值查找：Locate(T value)

初始条件：线性表存在。
操作结果：在线性表中查找值为value的数据元素，其结果返回在线性表中首次出现的值为value的数据元素的序号，称为查找成功；否则，在线性表中未找到值为value的数据元素，返回一个特殊值表示查找失败。

实际上，在.NET框架中，许多类的求长度、判断满和判断空等操作都用属性来表示，这里在接口中定义为方法是为了说明数据结构的操作运算。实际上，属性也是方法。在后面章节的数据结构如栈、队列等的处理也是如此，就不一一说明了。

顺序表

顺序表的定义

在计算机内，保存线性表最简单、最自然的方式，就是把表中的元素一个接一个地放进顺序的存储单元，这就是线性表的顺序存储（Sequence Storage）。线性表的顺序存储是指在内存中用一块地址连续的空间依次存放线性表的数据元素，用这种方式存储的线性表叫顺序表（Sequence List），如图2.1所示。顺序表的特点是表中相邻的数据元素在内存中存储位置也相邻。

图2.1 顺序表的存储结构示意图

假设顺序表中的每个数据元素占w个存储单元，设第i个数据元素的存储地址为Loc(a i )，则有：

式中的Loc(a 1 )表示第一个数据元素a 1 的存储地址，也是顺序表的起始存储地址，称为顺序表的基地址(Base Address)。也就是说，只要知道顺序表的基地址和每个数据元素所占的存储单元的个数就可以求出顺序表中任何一个数据元素的存储地址。并且，由于计算顺序表中每个数据元素存储地址的时间相同，所以顺序表具有随机存取的特点。

C#语言中的数组在内存中占用的存储空间就是一组连续的存储区域，因此，数组具有随机存取的特点。所以，数组天生具有表示顺序表的数据存储区域的特
性。

把顺序表看作是一个泛型类，类名叫SeqList\。”Seq”是英文单词”Sequence”的前三个字母。SeqList类实现了接口IListDS。用数组来存储顺序表中的元素，在 SeqList类中用字段 data 来表示。由于经常需要在顺序表中插入或删除数据元素，所以要求顺序表的表长是可变的。因此，数组的容量需要设计得特别大，可以用 System.Array 的 Length 属性来表示。但为了说明顺序表的最大长度（顺序表的容量），在 SeqList类中用字段 maxsize 来表示。

maxsize 的值可以根据实际需要修改，这通过SeqList类中构造器的参数 size来实现。顺序表中的元素由 data[0]开始依次顺序存放，由于顺序表中的实际元素个数一般达不到 maxsize，因此，在 SeqList类中需要一个字段 last 表示顺序表中最后一个数据元素在数组中的位置。如果顺序表中有数据元素时，last 的变化范围是0到maxsize-1，如果顺序表为空，last=-1。具体表示见图 2.1 所示。由于顺序表空间的限制，当往顺序表中插入数据元素需要判断顺序表是否已满，顺
序表已满不能插入元素。所以，SeqList类除了要实现接口 IListDS中的方法外，还需要实现判断顺序表是否已满等成员方法。

顺序表类 SeqList的实现说明如下所示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
public class SeqList<T> : IListDS<T> 
{
    private int maxsize; //顺序表的容量
    private T[] data; //数组，用于存储顺序表中的数据元素
    private int last; //指示顺序表最后一个元素的位置
    //索引器
    public T this[int index]
    {
        get
        {
            return data[index];
        }
        set
        {
            data[index] = value;
        }
    }

    //最后一个数据元素位置属性
    public int Last
    {
        get
        {
            return last;
        }
    }

    //容量属性
    public int Maxsize
    {
        get
        {
            return maxsize;
        }
        set
        {
            maxsize = value;
        }
    }

    //构造器
    public SeqList(int size)
    {
        data = new T[size];
        maxsize = size;
        last = -1;
    }

    //求顺序表的长度
    public int GetLength()
    {
        return last+1;
    }

    //清空顺序表
    public void Clear()
    {
        last = -1;
    }

    //判断顺序表是否为空
    public bool IsEmpty()
    {
        if (last == -1)
        {
            return true;
        }
        else
        {
            return false;
        }
    }

    //判断顺序表是否为满
    public bool IsFull()
    {
        if (last == maxsize-1)
        {
            return true;
        }
        else
        {
            return false;
        }
    }

    //在顺序表的末尾添加新元素
    public void Append(T item)
    {
        if(IsFull())
        {
            Console.WriteLine("List is full");
            return;
        }
        data[++last] = item;
    }

    //在顺序表的第i个数据元素的位置插入一个数据元素
    public void Insert(T item, int i)
    {
        if (IsFull())
        {
            Console.WriteLine("List is full");
            return;
        }
        if(i<1 || i>last+2)
        {
            Console.WriteLine("Position is error!");
            return;
        }
        if (i == last + 2)
        {
            data[last+1] = item;

        }
        else
        {
            for (int j = last; j>= i-1; --j)
            {
                data[j + 1] = data[j];
            }
            data[i-1] = item;
        }
        ++last;
    }

    //删除顺序表的第i个数据元素
    public T Delete(int i)
    {
        T tmp = default(T);
        if (IsEmpty())
        {
            Console.WriteLine("List is empty");
            return tmp;
        }
        if (i < 1 || i > last+1)
        {
            Console.WriteLine("Position is error!");
            return tmp;
        }
        if (i == last+1)
        {
            tmp = data[last--];
        }
        else
        {
            tmp = data[i-1];
            for (int j = i; j <= last; ++j)
            {
                data[j] = data[j + 1];
            }
        }
        --last;
        return tmp;
    }

    //获得顺序表的第i个数据元素
    public T GetElem(int i)
    {
        if (IsEmpty() || (i<1) || (i>last+1))
        {
            Console.WriteLine("List is empty or Position is error!");
            return default(T);
        }
        return data[i-1];
    }

    //在顺序表中查找值为value的数据元素
    public int Locate(T value)
    {
        if(IsEmpty())
        {
            Console.WriteLine("List is Empty!");
            return -1;
        }
        int i = 0;
        for (i = 0; i <= last; ++i)
        {
            if (value.Equals(data[i]))
            {
                break;
            }
        }
        if (i > last)
        {
            return -1;
        }
        return i;
    }
}

顺序表的基本操作实现

1、求顺序表的长度

由于数组是0基数组，即数组的最小索引为0，所以，顺序表的长度就是数组中最后一个元素的索引last加1。

求顺序表长度的算法实现如下：

1
2
3
4
public int GetLength()
{
    return last+1;
}

2、清空操作

清除顺序表中的数据元素是使顺序表为空，此时，last等于-1。
清空顺序表的算法实现如下：

1
2
3
4
public void Clear()
{
    last = -1;
}

3、判断线性表是否为空

如果顺序表的 last 为-1，则顺序表为空，返回 true，否则返回 false。
判断线性表是否为空的算法实现如下：

1
2
3
4
5
6
7
8
9
10
11
public bool IsEmpty()
{
if (last == -1)
{
return true;
}
else
{
return false;
}
}

4、判断顺序表是否为满
如果顺序表为满，last 等于 maxsize-1，则返回 true，否则返回 false。
判断顺序表是否为满的算法实现如下：

1
2
3
4
5
6
7
8
9
10
11
public bool IsFull()
{
    if (last == maxsize - 1)
    {
        return true;
    }
    else
    {
        return false;
    }
}

5、附加操作
附加操作是在顺序表未满的情况下，在表的末端添加一个新元素，然后使顺
序表的last加1。
附加操作的算法实现如下：

1
2
3
4
5
6
7
8
9
public void Append(T item)
{
    if(IsFull())
    {
        Console.WriteLine("List is full");
        return;
    }
    data[++last] = item;
}

6、插入操作

顺序表的插入是指在顺序表的第i个位置插入一个值为item的新元素，插入后使原表长为n的表 (a 1 ,a 2 , … ,a i-1 ,a i ,a i+1 , … ,a n ) 成为表长为n+1的表(a 1 ,a 2 ,…,a i-1 ,item,a i ,a i+1 ,…,a n )。i的取值范围为1≤i≤n+1，i为n+1时，表示在顺序表的末尾插入数据元素。

顺序表上插入一个数据元素的步骤如下：
（1）判断顺序表是否已满和插入的位置是否正确，表满或插入的位置不正确不能插入；
（2）如果表未满和插入的位置正确，则将a n ～a i 依次向后移动，为新的数据元素空出位置。在算法中用循环来实现；
（3）将新的数据元素插入到空出的第 i 个位置上；
（4）修改 last（相当于修改表长），使它仍指向顺序表的最后一个数据元素。

图 2.2 为顺序表的插入操作示意图。

单链表

顺序表是用地址连续的存储单元顺序存储线性表中的各个数据元素，逻辑上相邻的数据元素在物理位置上也相邻。因此，在顺序表中查找任何一个位置上的数据元素非常方便，这是顺序存储的优点。但是，在对顺序表进行插入和删除时，需要通过移动数据元素来实现，影响了运行效率。本节介绍线性表的另外一种存储结构——链式存储（Linked Storage），这样的线性表叫链表（Linked List）。链表不要求逻辑上相邻的数据元素在物理存储位置上也相邻，因此，在对链表进行插入和删除时不需要移动数据元素，但同时也失去了顺序表可随机存储的优点。

单链表的定义

链表是用一组任意的存储单元来存储线性表中的数据元素（这组存储单元可以是连续的，也可以是不连续的）。那么，怎么表示两个数据元素逻辑上的相邻关系呢？即如何表示数据元素之间的线性关系呢？为此，在存储数据元素时，除了存储数据元素本身的信息外，还要存储与它相邻的数据元素的存储地址信息。

这两部分信息组成该数据元素的存储映像（Image），称为结点（Node）。把存储据元素本身信息的域叫结点的数据域（Data Domain），把存储与它相邻的数据元素的存储地址信息的域叫结点的引用域（Reference Domain）。因此，线性表通过每个结点的引用域形成了一根“链条”，这就是“链表”名称的由来。

如果结点的引用域只存储该结点直接后继结点的存储地址，则该链表叫单链表（Singly Linked List）。把该引用域叫next。单链表结点的结构如图2.5所示，图中data表示结点的数据域。

图2.5 单链表的结点结构

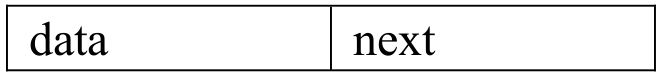
把单链表结点看作是一个类，类名为Node<T>。单链表结点类的实现如下所示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
public class Node<T>
{
    private T data; //数据域
    private Node<T> next; //引用域

    //构造器
    public Node(T val, Node<T> p)
    {
        data = val;
        next = p;
    }

    //构造器
    public Node(Node<T> p)
    {
        next = p;
    }

    //构造器
    //链表的最后一个结点
    public Node(T val)
    {
        data = val;
        next = null;
    }

    //构造器
    public Node()
    {
        data = default(T);
        next = null;
    }

    //数据域属性
    public T Data
    {
        get
        {
            return data;
        }
        set
        {
            data = value;
        }
    }

    //引用域属性
    public Node<T> Next
    {
        get
        {
            return next;
        }
        set
        {
            next = value;
        }
    }
}

图2.6是线性表(a1, a2, a3, a4, a5, a6)对应的链式存储结构示意图。

图2.6 链式存储结构示意图

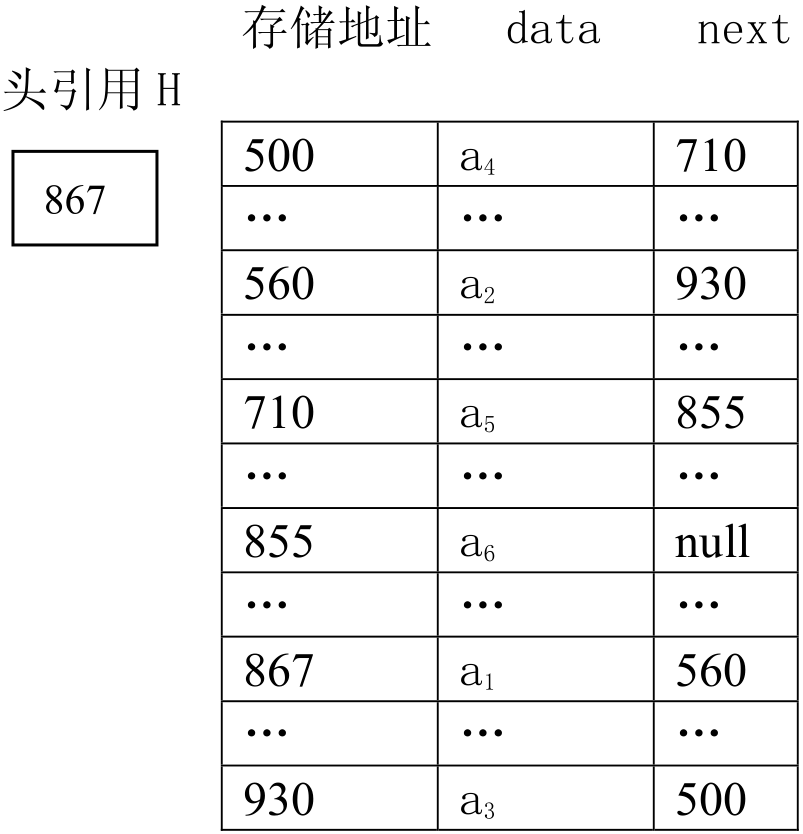
通常，我们把链表画成用箭头相连接的结点的序列，结点间的箭头表示引用域中存储的地址。为了处理上的简洁与方便，在本书中把引用域中存储的地址叫引用。图2.6中的链表用图2.7的形式表示。

图2.7 单链表示意图

由图2.7可知，单链表由头引用H唯一确定。头引用指向单链表的第一个结点，也就是把单链表第一个结点的地址放在H中，所以，H是一个Node类型的变量。头引用为null表示一个空表。

把单链表看作是一个类，类名叫LinkList<T>。LinkList<T>类也实现了接口IListDS<T>。LinkList<T>类有一个字段head，表示单链表的头引用，所以head的类型为Node<T>。由于链表的存储空间不是连续的，所以没有最大空间的限制，在链表中插入结点时不需要判断链表是否已满。因此，在LinkList<T>类中不需要实现判断链表是否已满的成员方法。

单链表类LinkList<T>的实现说明如下所示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
public class LinkList<T> : IListDS<T> 
{
    private Node<T> head; //单链表的头引用

    //头引用属性
    public Node<T> Head
    {
        get
        {
            return head;
        }
        set
        {
            head = value;
        }
    }

    //构造器
    public LinkList()
    {
        head = null;
    }

    //求单链表的长度
    public int GetLength()
    {
        Node<T> p = head;
        int len = 0;
        while (p != null)
        {
            ++len;
            p = p.Next;
        }
        return len;
    }

    //清空单链表
    public void Clear()
    {
        head = null;
    }

    //判断单链表是否为空
    public bool IsEmpty()
    {
        if (head == null)
        {
            return true;
        }
        else
        {
            return false;
        }
    }

    //在单链表的末尾添加新元素
    public void Append(T item)
    {
        Node<T> q = new Node<T>(item);
        Node<T> p = new Node<T>();
        if (head == null)
        {
            head = q;
            return;
        }
        p = head;
        while (p.Next != null)
        {
            p = p.Next;
        }
        p.Next = q;
    }

    //在单链表的第i个结点的位置前插入一个值为item的结点
    public void Insert(T item, int i)
    {
        if (IsEmpty() || i < 1)
        {
            Console.WriteLine( " List is empty or Position is error! " );
            return;
        }
        if (i == 1)
        {
            Node<T> q = new Node<T>(item);
            q.Next = head;
            head = q;
            return;
        }
        Node<T> p = head;
        Node<T> r = new Node<T>();
        int j = 1;
        while (p.Next != null&& j < i)
        {
            r = p;
            p = p.Next;
            ++j;
        }
        if (j == i)
        {
            Node<T> q = new Node<T>(item);
            q.Next = p;
            r.Next = q;
        }
    }

    //在单链表的第i个结点的位置后插入一个值为item的结点
    public void InsertPost(T item, int i)
    {
        if (IsEmpty() || i < 1)
        {
            Console.WriteLine( " List is empty or Position is error! " );
            return;
        }
        if (i == 1)
        {
            Node<T> q = new Node<T>(item);
            q.Next = head.Next;
            head.Next = q;
            return;
        }
        Node<T> p = head;
        int j = 1;
        while (p != null&& j < i)
        {
            p = p.Next;
            ++j;
        }
        if (j == i)
        {
            Node<T> q = new Node<T>(item);
            q.Next = p.Next;
            p.Next = q;
        }
    }

    //删除单链表的第i个结点
    public T Delete(int i)
    {
        if (IsEmpty()|| i < 0)
        {
            Console.WriteLine("Link is empty or Position is error!");
            return default(T);
        }
        Node<T> q = new Node<T>();

        if (i == 1)
        {
            q = head;
            head = head.Next;
            return q.Data;
        }
        Node<T> p = head;
        int j = 1;
        while (p.Next != null&& j < i)
        {
            ++j;
            q = p;
            p = p.Next;
        }
        if (j == i)
        {
            q.Next = p.Next;
            return p.Data;
        }
        else
        {
            Console.WriteLine("The ith node is not exist!");
            return default(T);
        }
    }

    //获得单链表的第i个数据元素
    public T GetElem(int i)
    {
        if (IsEmpty())
        {
            Console.WriteLine("List is empty!");
            return default(T);
        }
        Node<T> p = new Node<T>();
        p = head;
        int j = 1;
        while (p.Next != null&& j < i)
        {
            ++j;
            p = p.Next;
        }
        if (j == i)
        {
            return p.Data;
        }
        else
        {
            Console.WriteLine("The ith node is not exist!");
            return default(T);
        }
    }

    //在单链表中查找值为value的结点
    public int Locate(T value)
    {
        if(IsEmpty())
        {
            Console.WriteLine("List is Empty!");
            return -1;
        }
        Node<T> p = new Node<T>();
        p = head;
        int i = 1;
        while (!p.Data.Equals(value)&& p.Next != null)
        {
            P = p.Next;
            ++i;
        }
        return i;
    }
}

单链表的基本操作实现

1、求单链表的长度

求单链表的长度与顺序表不同。顺序表可以通过指示表中最后一个数据元素的last直接求得，因为顺序表所占用的空间是连续的空间，而单链表需要从头引用开始，一个结点一个结点遍历，直到表的末尾。

求单链表长度的算法实现如下：

1
2
3
4
5
6
7
8
9
10
11
public int GetLength()
{
    Node<T> p = head;
    int len = 0;
    while (p != null)
    {
        ++len;
        p = p.Next;
    }
    return len;
}

时间复杂度分析：求单链表的长度需要遍历整个链表，所以，时间复杂度为O(n)，n是单链表的长度。

2、清空操作

清空操作是指清除单链表中的所有结点使单链表为空，此时，头引用head为null。

清空单链表的算法实现如下：

1
2
3
4
public void Clear()
{
    head = null;
}

需要注意的是，单链表清空之后，原来结点所占用的空间不会一直保留，而由垃圾回收器进行回收，不用程序员自己处理。这和顺序表的清空操作不一样。

顺序表的清空操作需要last被置为-1，但为数组分配的空间仍然保留，因为顺序表需要一片连续的空间，而单链表不需要。

3、判断单链表是否为空

如果单链表的头引用为null，则单链表为空，返回true，否则返回false。

判断单链表是否为空的算法实现如下：

1
2
3
4
5
6
7
8
9
10
11
public bool IsEmpty()
{
    if (head == null)
    {
        return true;
    }
    else
    {
        return false;
    }
}

4、附加操作

单链表的附加操作也需要从单链表的头引用开始遍历单链表，直到单链表的末尾，然后在单链表的末端添加一个新结点。

附加操作的算法实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public void Append(T item)
{
    Node<T> q = new Node<T>(item);
    Node<T> p = new Node<T>();
    if (head == null)
    {
        head = q;
        return;
    }
    p = head;
    while (p.Next != null)
    {
        p = p.Next;
    }
    p.Next = q;
}

算法的时间复杂度分析：单链表的附加操作需要遍历到最后一个结点，所以，附加操作的时间复杂度为O(n)，n是单链表的长度。

5、插入操作

单链表的插入操作是指在表的第i个位置结点处插入一个值为item的新结点。插入操作需要从单连表的头引用开始遍历，直到找到第i个位置的结点。插入操作分为在结点之前插入的前插操作和在结点之后插入的后插操作。

（1）前插操作

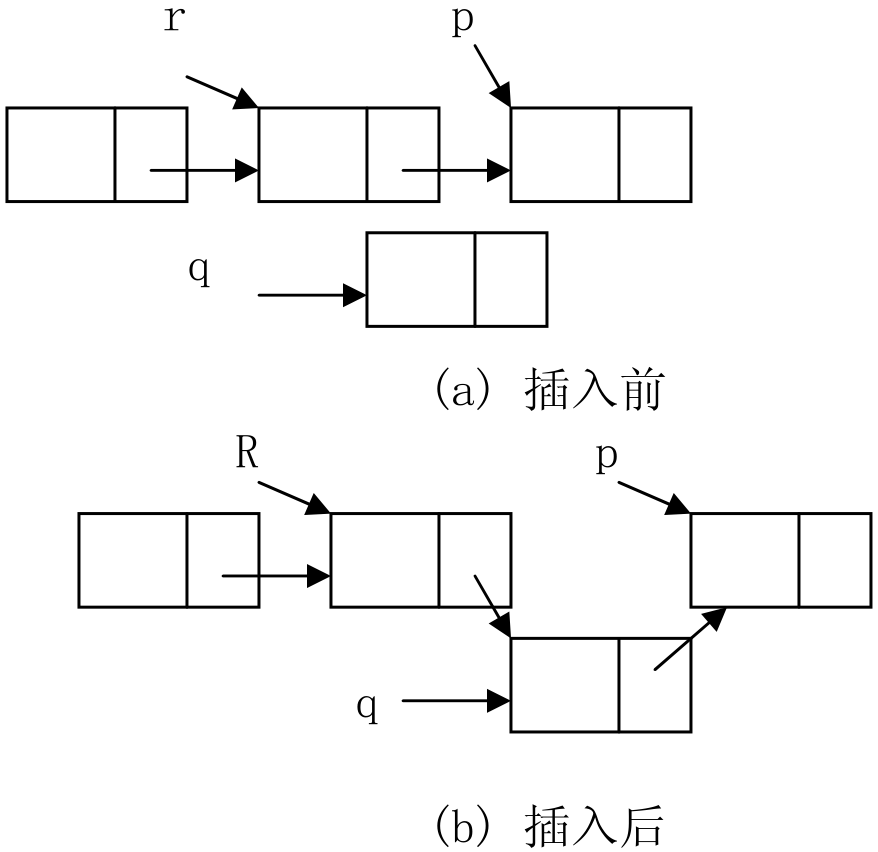
前插操作需要查找第i个位置的结点的直接前驱。设p指向第i个位置的结点，q指向待插入的新结点，r指向p的直接前驱结点，将q插在p之前的操作如图2.8所示。如果要在第一个结点之前插入新结点，则需要把p结点的地址保存在q的引用域中，然后把p的地址保存在头引用中。

图2.8 单链表的前插操作示意图

单链表的前插操作的算法实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public void Insert(T item, int i)
{
    if (IsEmpty() || i < 1)
    {
        Console.WriteLine(“List is empty or Position is error!”);
        return;
    }
    if (i == 1)
    {
        Node<T> q = new Node<T>(item);
        q.Next = head;
        head = q;
        return;
    }
    Node<T> p = head;
    Node<T> r = new Node<T>();
    int j = 1;
    while (p.Next != null&& j < i)
    {
        r = p;
        p = p.Next;
        ++j;
    }
    if (j == i)
    {
        Node<T> q = new Node<T>(item);
        q.Next = p;
        r.Next = q;
    }
    else
    {
        Console.Writeline(“Position is error!”);
    }
    return;
}

（2）后插操作

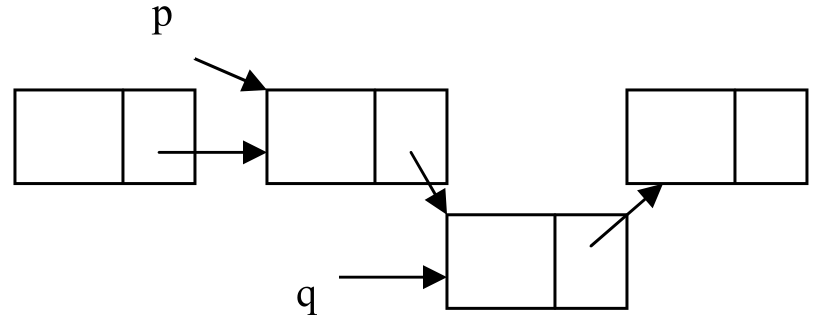
设p指向第i个位置的结点，q指向待插入的新结点，将q插在p之后的操作示意图如图2.9所示。

图2.9 单链表的后插操作示意图
（a）插入前

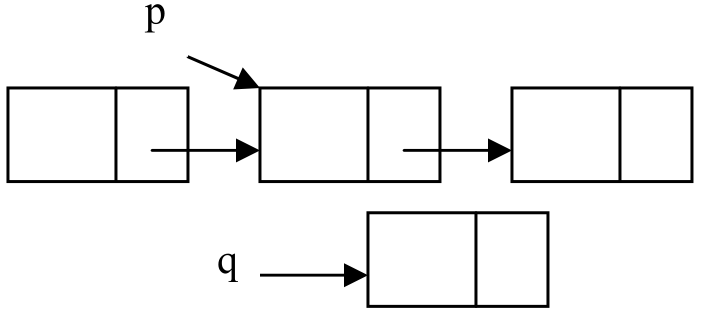
（b）插入后

单链表的后插操作的算法实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public void InsertPost(T item, int i)
{
    if (IsEmpty() || i < 1)
    {
        Console.WriteLine(“List is empty or Position is error!”);
        return;
    }
    if (i == 1)
    {
        Node<T> q = new Node<T>(item);
        q.Next = head.Next;
        head.Next = q;
        return;
    }
    Node<T> p = head;
    int j = 1;
    while (p.Next != null&& j < i)
    {
        p = p.Next;
        ++j;
    }
    if (j == i)
    {
        Node<T> q = new Node<T>(item);
        q.Next = p.Next;
        p.Next = q;
    }
    else
    {
        Console.WriteLine(“Position is error!”);
    }
    return;
}

算法的时间复杂度分析：从前插和后插运算的算法可知，在第i个结点处插入结点的时间主要消耗在查找操作上。由上面几个操作可知，单链表的查找需要从头引用开始，一个结点一个结点遍历，因为单链表的存储空间不是连续的空间。

这是单链表的缺点，而是顺序表的优点。找到目标结点后的插入操作很简单，不需要进行数据元素的移动，因为单链表不需要连续的空间。删除操作也是如此，这是单链表的优点，相反是顺序表的缺点。遍历的结点数最少为1个，当i等于1时，最多为n，n为单链表的长度，平均遍历的结点数为n/2。所以，插入操作的时间复杂度为O(n)。

因此，线性表的顺序存储和链式存储各有优缺点，线性表如何存储取决于使用的场合。如果不需要经常在线性表中进行插入和删除，只是进行查找，那么，线性表应该顺序存储；如果线性表需要经常插入和删除，而不经常进行查找，则线性表应该链式存储。

6、删除操作

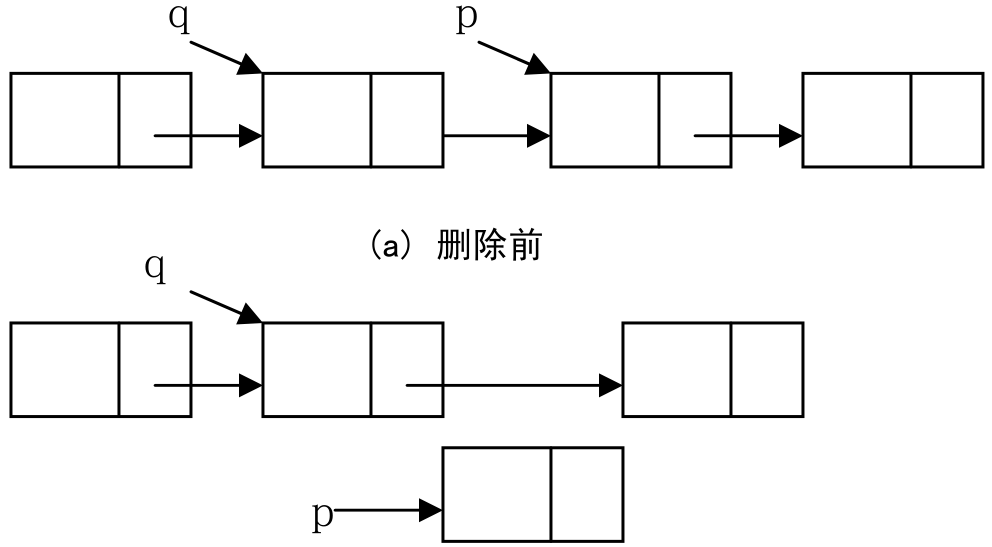
单链表的删除操作是指删除第i个结点，返回被删除结点的值。删除操作也需要从头引用开始遍历单链表，直到找到第i个位置的结点。如果i为1，则要删除第一个结点，则需要把该结点的直接后继结点的地址赋给头引用。对于其它结点，由于要删除结点，所以在遍历过程中需要保存被遍历到的结点的直接前驱，找到第i个结点后，把该结点的直接后继作为该结点的直接前驱的直接后继。

删除操作如图2.10所示。

图2.10 单链表的删除操作示意图

删除操作的算法实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public T Delete(int i)
{
    if (IsEmpty()|| i < 0)
    {
        Console.WriteLine("Link is empty or Position is error!");
        return default(T);
    }
    Node<T> q = new Node<T>();
    if (i == 1)
    {
        q = head;
        head = head.Next;
        return q.Data;
    }
    Node<T> p = head;
    int j = 1;
    while (p.Next != null&& j < i)
    {
        ++j;
        q = p;
        p = p.Next;
    }
    if (j == i)
    {
        q.Next = p.Next;
        return p.Data;
    }
    else
    {
        Console.WriteLine("The ith node is not exist!");
        return default(T);
    }
}

算法的时间复杂度分析：单链表上的删除操作与插入操作一样，时间主要消耗在结点的遍历上。如果表为空则不进行遍历。当表非空时，删除第i个位置的结点，i等于1遍历的结点数最少（1个），i等于n遍历的结点数最多（n个，n为单链表的长度），平均遍历的结点数为n/2。所以，删除操作的时间复杂度为O(n)。

7、取表元

取表元运算是返回单链表中第i个结点的值。与插入操作一样，时间主要消耗在结点的遍历上。如果表为空则不进行遍历。当表非空时，i等于1遍历的结点数最少（1个），i等于n遍历的结点数最多（n个，n为单链表的长度），平均遍历的结点数为n/2。所以，取表元运算的时间复杂度为O(n)。

取表元运算的算法实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public T GetElem(int i)
{
    if (IsEmpty())
    {
        Console.WriteLine("List is empty!");
        return default(T);
    }
    Node<T> p = new Node<T>();
    p = head;
    int j = 1;
    while (p.Next != null&& j < i)
    {
        ++j;
        p = p.Next;
    }
    if (j == i)
    {
        return p.Data;
    }
    else
    {
        Console.WriteLine("The ith node is not exist!");
        return default(T);
    }
}

8、按值查找

单链表中的按值查找是指在表中查找其值满足给定值的结点。由于单链表的存储空间是非连续的，所以，单链表的按值查找只能从头引用开始遍历，依次将被遍历到的结点的值与给定值比较，如果相等，则返回在单序表中首次出现与给定值相等的数据元素的序号，称为查找成功；否则，在单链表中没有值与给定值匹配的结点，返回一个特殊值表示查找失败。

按值查找运算的算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public int Locate(T value)
{
    if(IsEmpty())
    {
        Console.WriteLine("List is Empty!");
        return -1;
    }
    Node<T> p = new Node<T>();
    p = head;
    int i = 1;
    while (!p.Data.Equals(value)&& p.Next != null)
    {
        P = p.Next;
        ++i;
    }
    return i;
}

算法的时间复杂度分析：单链表中的按值查找的主要运算是比较，比较的次数与给定值在表中的位置和表长有关。当给定值与第一个结点的值相等时，比较次数为1；当给定值与最后一个结点的值相等时，比较次数为n。所以，平均比较次数为(n+1)/2，时间复杂度为 O(n)。

9、单链表的建立

单链表的建立与顺序表的建立不同，它是一种动态管理的存储结构，链表中的每个结点占用的存储空间不是预先分配，而是运行时系统根据需求而生成的。单链表的建立分为在头部插入结点建立单链表和在尾部插入结点建立单链表。由于要读入数据元素，下面以整数为例分别对这两种情况进行讨论。

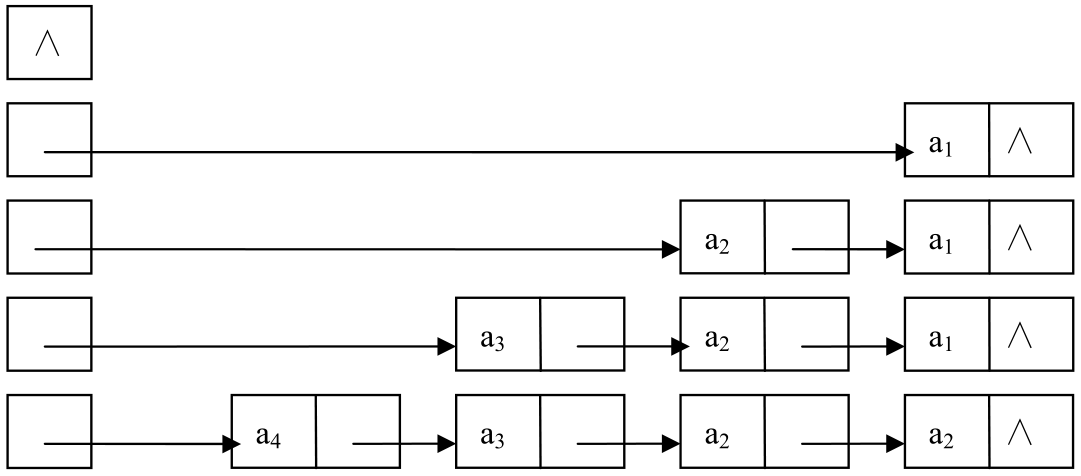
（1）在单链表的头部插入结点建立单链表

建立单链表从空表开始，每读入一个数据元素就申请一个结点，然后插在链表的头部。图2.11 展现了线性表(a1, a2, a3, a4)的链表建立过程。因为是在链表的头部插入，读入数据的顺序和链表中的逻辑顺序是相反的。

图2.11 在头部插入结点建立单链表

在头部插入结点建立单链表的算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
LinkList<int> CreateLListHead()
{
    int d;
    LinkList<int> L = new LinkList<int>();
    d = Int32.Parse(Console.ReadLine());
    while (d != -1)
    {
        Node<int> p = new Node<int>(d);
        p.Next = L.Head;
        L.Head = p;

        d = Int32.Parse(Console.ReadLine());
    }
    return L;
}

-1是输入数据的结束标志，当输入的数为-1时，表示输入结束，当然也可以根据需求用其它数作为结束标志。

（2）在单链表的尾部插入结点建立单链表

头部插入结点建立单链表简单，但读入的数据元素的顺序与生成的链表中元素的顺序是相反的。若希望次序一致，则用尾部插入的方法。因为每次是将新结点插入到链表的尾部，所以需加入一个引用R用来始终指向链表中的尾结点，以便能够将新结点插入到链表的尾部。图2.12展现了在链表的尾部插入结点建立单链表的过程。

图2.12 在尾部插入结点建立单链表

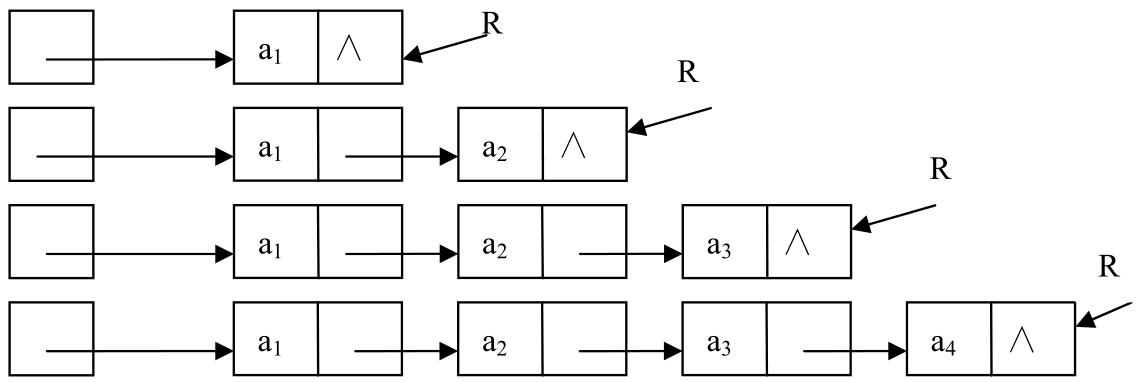
算法思路：初始状态时，头引用head为null，尾引用R为null。按线性表中元素的顺序依次读入数据元素，不是结束标志时，申请结点，将新结点插入到R所指结点的后面，然后R指向新结点。

在尾部插入结点建立单链表的算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
LinkList<int> CreateListTail()
{
    Node<int> R = new Node<int>();
    int d;
    LinkList<int> L = new LinkList<int>();
    R = L.Head;
    d = Int32.Parse(Console.ReadLine());
    while (d != -1)
    {
        Node<int> p = new Node<int>(d);
        if (L.Head == null)
        {
            L.Head = p;
        }
        else
        {
            R.Next = p;
        }
        R = p;
        d = Int32.Parse(Console.ReadLine());
    }
    if (R != null)
    {
        R.Next = null;
    }
    return L;
}

-1是输入数据的结束标志，当输入的数为-1时，表示输入结束，当然也可以根据需求用其它数作为结束标志。

在上面的算法中，第一个结点的处理和其它结点是不同的，原因是第一个结点加入时链表为空，它没有直接前驱结点，它的地址存放在链表的头引用中；而其它结点有直接前驱结点，其地址放在直接前驱结点的引用域中。在头部插入结点建立单链表的算法中，头引用所指向的结点也是变化的。“第一个结点”的问题在很多操作中都会遇到，如前面讲的在链表中插入结点和删除结点。为了方便处理，其解决办法是让头引用保存的结点地址不变。因此，在链表的头部加入了一个叫头结点（Head Node）的结点，把头结点的地址保存在头引用中。这样，即使是空表，头引用变量也不为空。头结点的加入使得“第一个结点”的问题不再存在，也使得“空表”和“非空表”的处理一致。

头结点的加入完全是为了操作的方便，它的数据域无定义，引用域存放的是第一个结点的地址，空表时该引用域为空。图2.13是带头结点的单链表空表和非空表的示意图。

图2.13 带头结点的单链表

单链表带头结点和不带头结点，操作有所不同，上面讲的操作都是不带头结点的操作。例如：带头结点的单链表的长度是不带头结点的单链表的长度加1。

在需要遍历单链表时，不带头结点的单链表是把头引用head赋给一个结点变量，即p=head，p为结点变量;而带头结点的单链表是把head的引用域赋给一个结点变量，即p=head.Next，p为结点变量。

例题中的单链表若没有特别说明，都是指带头结点的单链表。

单链表应用举例

【例2-4】已知单链表H，写一算法将其倒置，即实现如图2.14所示的操作，其中(a)为倒置前，(b)为倒置后。

图2.14 单链表的倒置

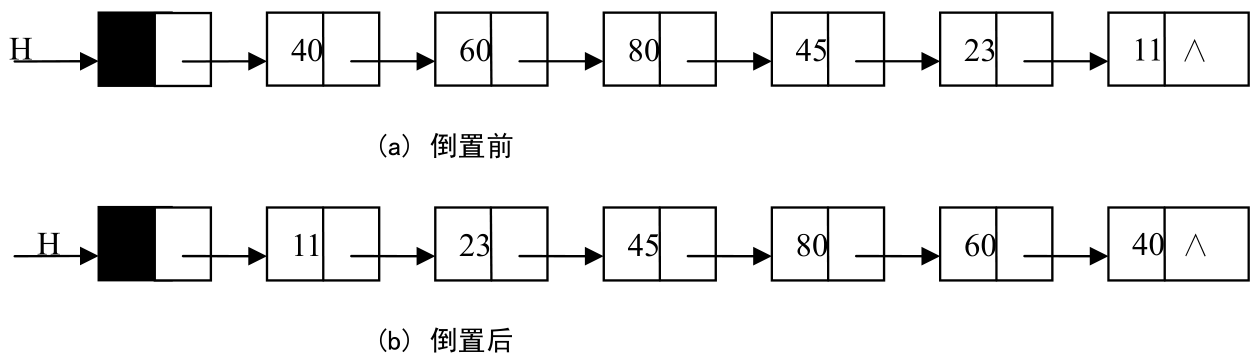
算法思路：由于单链表的存储空间不是连续的，所以，它的倒置不能像顺序表那样，把第i个结点与第n-i个结点交换（i的取值范围是1到n/2，n为单链表的长度）。其解决办法是依次取单链表中的每个结点插入到新链表中去。并且，为了节省内存资源，把原链表的头结点作为新链表的头结点。

存储整数的单链表的倒置的算法实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public void ReversLinkList(LinkList<int> H)
{
    Node<int> p = H.Next;
    Node<int> q = new Node<int>();
    H.Next = null;

    while (p != null)
    {
        q = p;
        p = p.Next;
        q.Next = H.Next;
        H.Next = q;
    }
}

该算法要对链表中的结点顺序扫描一遍才完成了倒置，所以时间复杂度为O(n)，但比同样长度的顺序表多花一倍的时间，因为顺序表只需要扫描一半的数据元素。

同样，该操作也可以作为LinkList类的一个成员方法。倒置方法在单链表类LinkList中的实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class LinkList<T> : IListDS<T> 
{
    ……
    public void Reverse()
    {
        Node<int> p = head.Next;
        Node<int> q = new Node<int>();
        head.Next = null;

        while (p != null)
        {
            q = p;
            p = p.Next;
            q.Next = head.Next;
            head.Next = q;
        }
    }
}

【例2-5】有数据类型为整型的单链表Ha和Hb，其数据元素均按从小到大的升序排列，编写一个算法将它们合并成一个表 Hc，要求 Hc 中结点的值也是升序排列。

算法思路：把 Ha 的头结点作为 Hc 的头结点，依次扫描 Ha 和 Hb 的结点，比较 Ha 和 Hb 当前结点数据域的值，将较小值的结点附加到Hc的末尾，如此直到一个单链表被扫描完，然后将未完的那个单链表中余下的结点附加到Hc的末尾即可。

将两表合并成一表的算法实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public LinkList<int> Merge(Linklist<int> Ha, LinkList<int> Hb)
{
    LinkList<int> Hc = new LinkList<int>();
    Node<int> p = Ha.Next;
    Node<int> q = Hb.Next;
    Node<int> s = Node<int>();
    Hc = Ha;
    Hc.Next = null;
    while (p != null && q != null)
    {
        if (p.Data < q.Data)
        {
            s = p;
            p = p.Next;
        }
        else
        {
            s = q;
            q = q.Next;
        }
        Hc.Append(s);
    }
    if (p == null)
    {
        p = q;
    }
    while (p != null)
    {
        s = p;
        p = p.Next;
        Hc.Append(s);
    }
    return Hc;
}

算法的时间复杂度是 O((m+n)*k)，m 是 Ha 的表长，n 是 Hb 的表长，k 是Hc 的表长。

从上面的算法可知，把结点附加到单链表的末尾是非常花时间的，因为定位最后一个结点需要从头结点开始遍历。而把结点插入到单链表的头部要节省很多时间，因为这不需要遍历链表。但由于是把结点插入到头部，所以得到的单链表是逆序排列而不是升序排列。

把结点插入到链表 Hc 头部合并 Ha 和 Hb 的算法实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public LinkList<int> Merge(Linklist<int> Ha, LinkList<int> Hb)
{
LinkList<int> Hc = new LinkList<int>();
Node<int> p = Ha.Next;
Node<int> q = Hb.Next;
Node<int> s = Node<int>();
Hc = Ha;
Hc.Next = null;
//两个表非空
while (p != null && q != null)
{
if (p.Data < q.Data)
{
s = p;
p = p.Next;
}
else
{
s = q;
q = q.Next;
}
s.Next = Hc.Next;
Hc.Next = s;
}
//第2个表非空而第1个表为空
if (p == null)
{
p = q;
}
//将两表中的剩余数据元素附加到新表的末尾
while (p != null)
{
s = p;
p = p.Next;
s.Next = Hc.Next;
Hc.Next = s;
}
return Hc;
}

算法的时间复杂度是 O(m+n)，m 是 Ha 的表长，n 是 Hb 的表长。

【例 2-6】已知一个存储整数的单链表 Ha，试构造单链表 Hb，要求单链表Hb中只包含单链表 Ha 中所有值不相同的结点。

算法思路：先申请一个结点作为 Hb的头结点，然后把Ha的第1个结点插入到Hb的头部，然后从 Ha 的第 2 个结点起，每一个结点的数据域的值与Hb中的每一个结点的数据域的值进行比较，如果不相同，则把该结点插入到Hb的头部。

删除单链表中相同值的结点的算法实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public LinkList<int> Purge(LinkList<int> Ha)
{
LinkList<int> Hb = new LinkList<int>();
Node<int> p = Ha.Next;
Node<int> q = new Node<int>();
Node<int> s = new Node<int>();
s = p;
p = p.Next;
s.Next = null;
Hb.Next = s;
while (p != null)
{
s = p;
p = p.Next;
q = Hb.Next;
while (q != null && q.Data != s.Data)
{
    q = q.Next;
}
if(q == null)
{
s.Next = Hb.Next;
Hb.Next = s;
}
}
return Hb;
}

算法的时间复杂度是 O(m+n)，m 是 Ha 的表长，n 是 Hb 的表长。

0%