思考并回答以下问题:
本章内容
- 学习分而治之。有时候,你可能会遇到使用任何已知的算法都无法解决的问题。优秀的算法学家遇到这种问题时,不会就此放弃,而是尝试使用掌握的各种问题解决方法来找出解决方案。分而治之是你学习的第一种通用的问题解决方法。
- 学习快速排序——一种常用的优雅的排序算法。快速排序使用分而治之的策略。
前一章深入介绍了递归,本章的重点是使用学到的新技能来解决问题。我们将探索分而治之(divide and conquer,D&C)——一种著名的递归式问题解决方法。
本书将深入算法的核心。只能解决一种问题的算法毕竟用处有限,而D&C提供了解决问题的思路,是另一个可供你使用的工具。面对新问题时,你不再束手无策,而是自问:“使用分而治之能解决吗?”
在本章末尾,你将学习第一个重要的D&C算法——快速排序。快速排序是一种排序算法,速度比第2章介绍的选择排序快得多,实属优雅代码的典范。
分而治之
D&C并不那么容易掌握,我将通过三个示例来介绍。首先,介绍一个直观的示例;然后,介绍一个代码示例,它不那么好看,但可能更容易理解;最后,详细介绍快速排序——一种使用D&C的排序算法。
假设你是农场主,有一小块土地。

你要将这块地均匀地分成方块,且分出的方块要尽可能大。显然,下面的分法都不符合要求。

如何将一块地均匀地分成方块,并确保分出的方块是最大的呢?使用D&C策略!D&C算法是递归的。使用D&C解决问题的过程包括两个步骤。
(1) 找出基线条件,这种条件必须尽可能简单。
(2) 不断将问题分解(或者说缩小规模),直到符合基线条件。
下面就来使用D&C找出前述问题的解决方案。可你能使用的最大方块有多大呢?
首先,找出基线条件。最容易处理的情况是,一条边的长度是另一条边的整数倍。
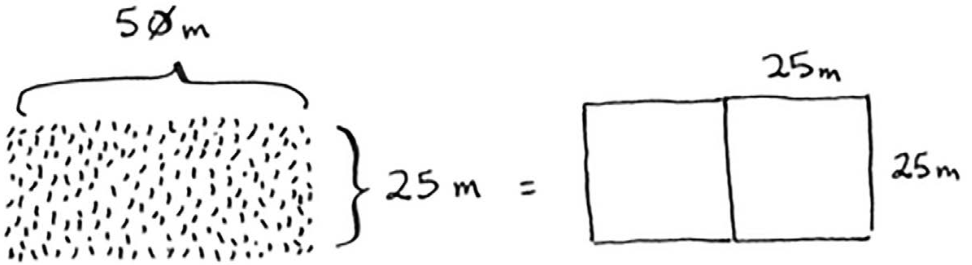
如果一边长25m,另一边长50m,那么可使用的最大方块为25m×25m。换言之,可以将这块地分成两个这样的方块。
现在需要找出递归条件,这正是D&C的用武之地。根据D&C的定义,每次递归调用都必须缩小问题的规模。如何缩小前述问题的规模呢?我们首先找出这块地可容纳的最大方块。
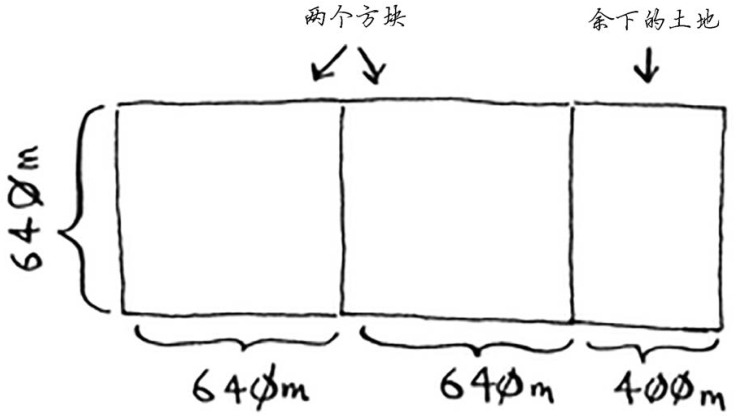
你可以从这块地中划出两个640m×640m的方块,同时余下一小块地。现在是顿悟时刻:何
不对余下的那一小块地使用相同的算法呢?
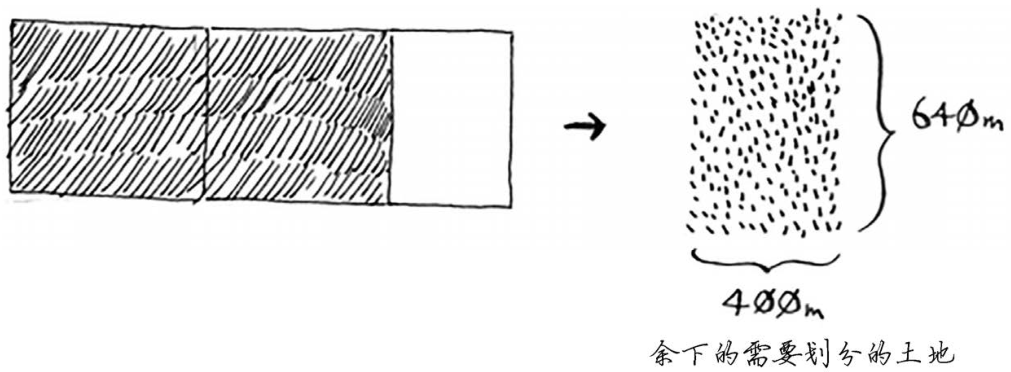
最初要划分的土地尺寸为1680m×640m,而现在要划分的土地更小,为640m×400m。适用于这小块地的最大方块,也是适用于整块地的最大方块。换言之,你将均匀划分1680m×640m土地的问题,简化成了均匀划分640m×400m土地的问题!
欧几里得算法
前面说“适用于这小块地的最大方块,也是适用于整块地的最大方块”,如果你觉得这一点不好理解,也不用担心。这确实不好理解,但遗憾的是,要证明这一点,需要的篇幅有点长,在本书中无法这样做,因此你只能选择相信这种说法是正确的。如果你想搞明白其中的原因,可参阅欧几里得算法。
下面再次使用同样的算法。对于640m×400m的土地,可从中划出的最大方块为400m×400m。
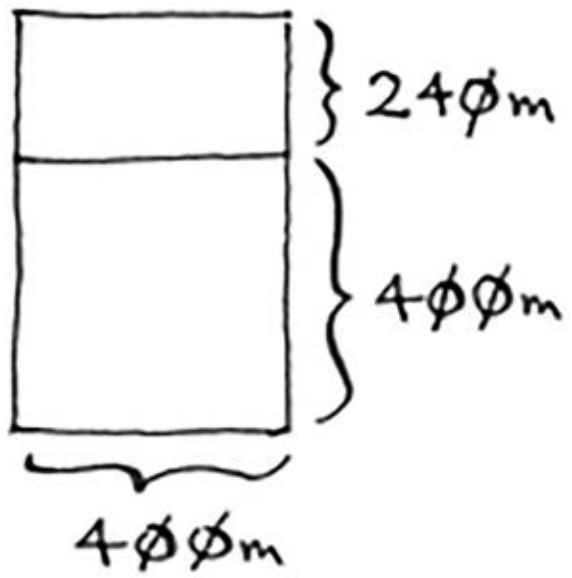
这将余下一块更小的土地,其尺寸为400m×240m。

你可从这块土地中划出最大的方块,余下一块更小的土地,其尺寸为240m×160m。
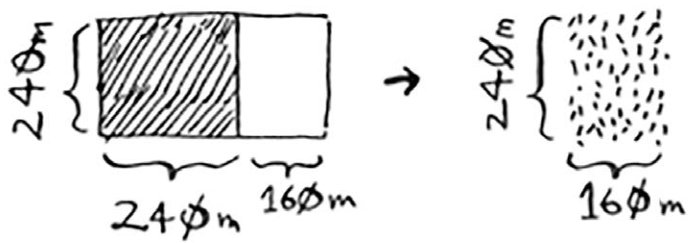
接下来,从这块土地中划出最大的方块,余下一块更小的土地。

余下的这块土地满足基线条件,因为160是80的整数倍。将这块土地分成两个方块后,将不会余下任何土地!

因此,对于最初的那片土地,适用的最大方块为80m×80m。
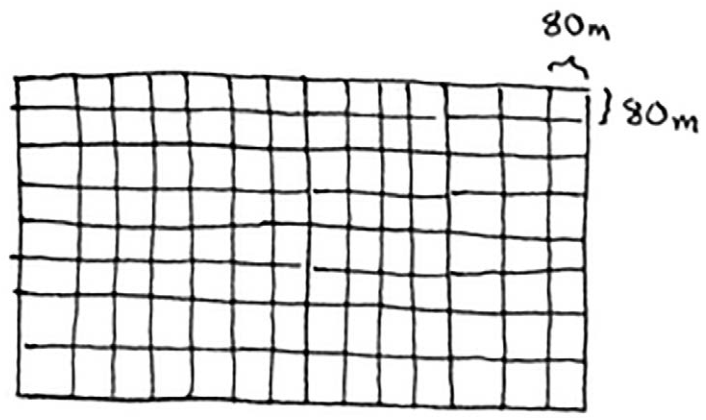
这里重申一下D&C的工作原理:
(1) 找出简单的基线条件;
(2) 确定如何缩小问题的规模,使其符合基线条件。
D&C并非可用于解决问题的算法,而是一种解决问题的思路。我们再来看一个例子。
给定一个数字数组。
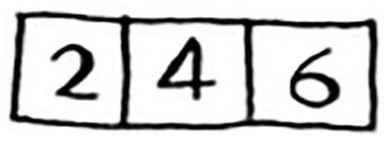
你需要将这些数字相加,并返回结果。使用循环很容易完成这种任务。
1 | def sum(arr): |
但如何使用递归函数来完成这种任务呢?
第一步:找出基线条件。最简单的数组什么样呢?请想想这个问题,再接着往下读。如果数组不包含任何元素或只包含一个元素,计算总和将非常容易。

因此这就是基线条件。
第二步:每次递归调用都必须离空数组更近一步。如何缩小问题的规模呢?下面是一种办法。
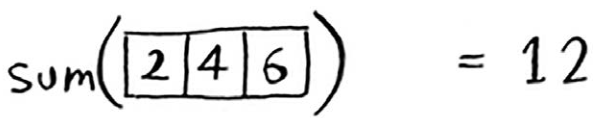
这与下面的版本等效。
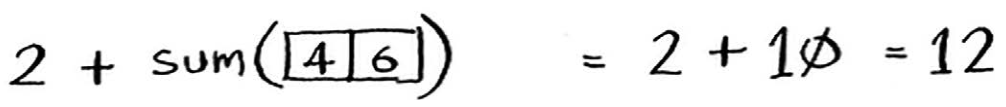
这两个版本的结果都为12,但在第二个版本中,给函数sum传递的数组更短。换言之,这缩小了问题的规模!
函数sum的工作原理类似于下面这样。

这个函数的运行过程如下。
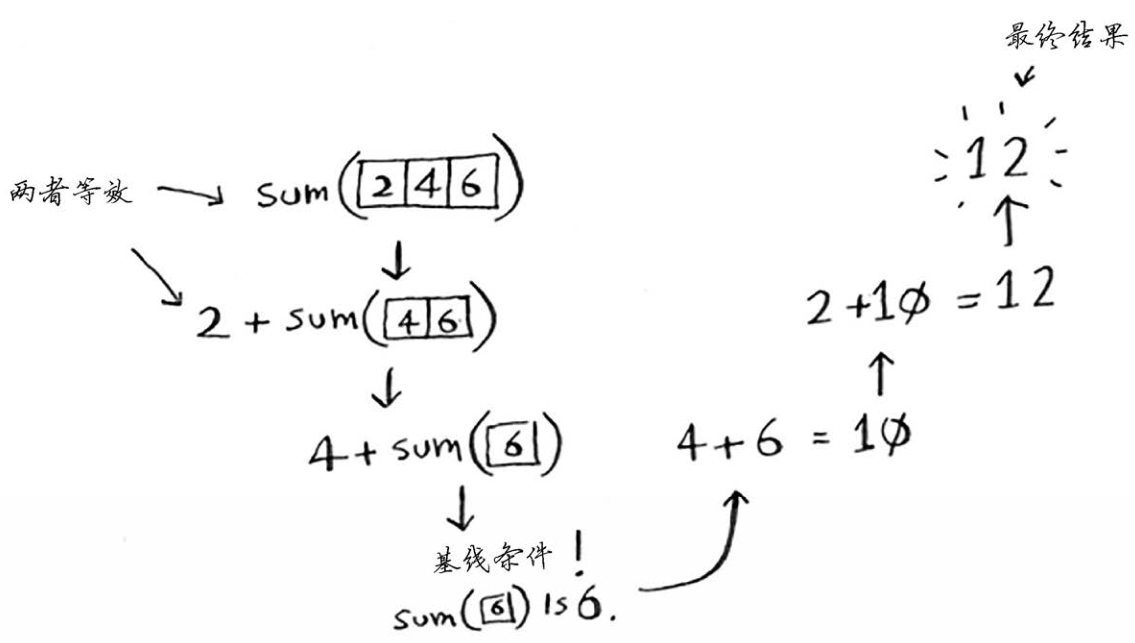
别忘了,递归记录了状态。
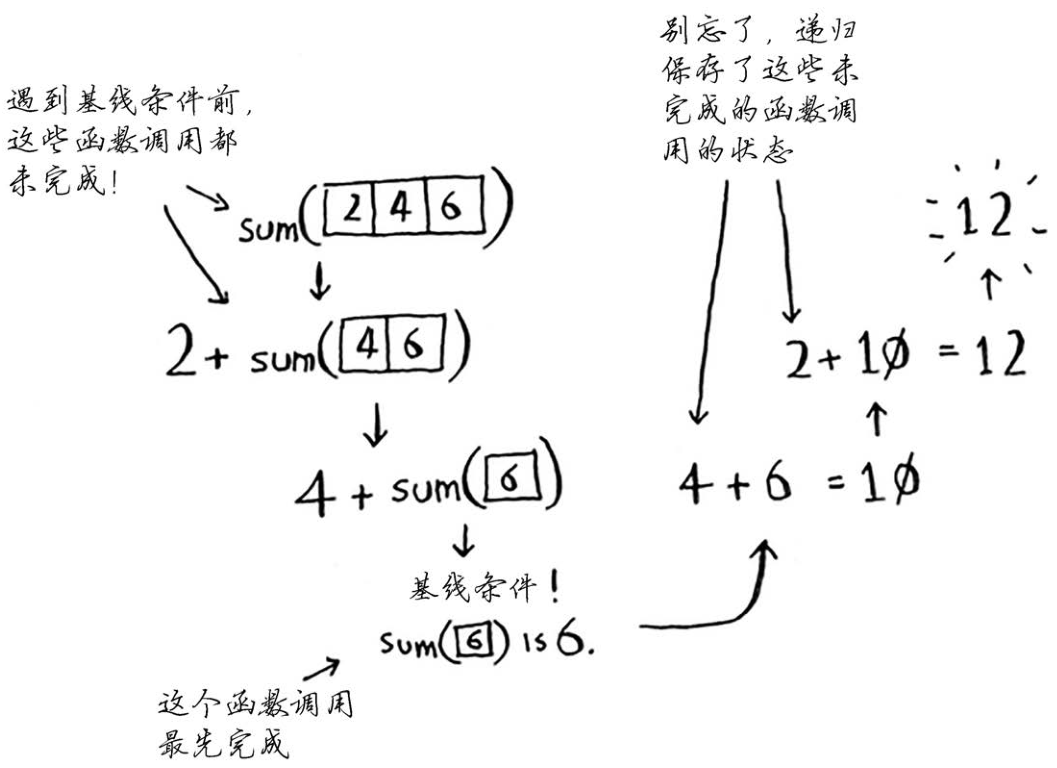
提 示
编写涉及数组的递归函数时,基线条件通常是数组为空或只包含一个元素。陷入困境时,请检查基线条件是不是这样的。
函数式编程一瞥
你可能想,既然使用循环可轻松地完成任务,为何还要使用递归方式呢?看看函数式编程你就明白了!诸如Haskell等函数式编程语言没有循环,因此你只能使用递归来编写这样的函数。如果你对递归有深入的认识,函数式编程语言学习起来将更容易。例如,使用Haskell时,你可能这样编写函数sum。1
2sum [] = 0 # 基线条件
sum (x:xs) = x + (sum xs) # 递归条件
注意,这就像是你有函数的两个定义。符合基线条件时运行第一个定义,符合递归条件时运行第二个定义。也可以使用Haskell语言中的if语句来编写这个函数。1
2
3sum arr = if arr == []
then 0
else (head arr) + (sum (tail arr))
但前一个版本更容易理解。Haskell大量使用了递归,因此它提供了各种方便实现递归的语法。如果你喜欢递归或想学习一门新语言,可以研究一下Haskell。
练习
1.请编写前述sum函数的代码。
2.编写一个递归函数来计算列表包含的元素数。
3.找出列表中最大的数字。
4.还记得第1章介绍的二分查找吗?它也是一种分而治之算法。你能找出二分查找算法的基线条件和递归条件吗?
快速排序
快速排序是一种常用的排序算法,比选择排序快得多。例如,C语言标准库中的函数qsort实现的就是快速排序。快速排序也使用了D&C。
下面来使用快速排序对数组进行排序。对排序算法来说,最简单的数组什么样呢?还记得前一节的“提示”吗?就是根本不需要排序的数组。
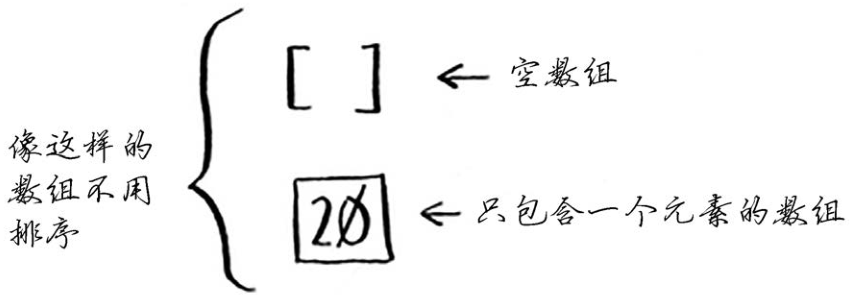
因此,基线条件为数组为空或只包含一个元素。在这种情况下,只需原样返回数组——根本就不用排序。1
2
3def quicksort(array):
if len(array) < 2:
return array
我们来看看更长的数组。对包含两个元素的数组进行排序也很容易。

包含三个元素的数组呢?

别忘了,你要使用D&C,因此需要将数组分解,直到满足基线条件。下面介绍快速排序的工作原理。首先,从数组中选择一个元素,这个元素被称为基准值(pivot)。
稍后再介绍如何选择合适的基准值。我们暂时将数组的第一个元素用作基准值。
接下来,找出比基准值小的元素以及比基准值大的元素。

这被称为分区(partitioning)。现在你有:
- 一个由所有小于基准值的数字组成的子数组;
- 基准值;
- 一个由所有大于基准值的数组组成的子数组。
这里只是进行了分区,得到的两个子数组是无序的。但如果这两个数组是有序的,对整个数组进行排序将非常容易。
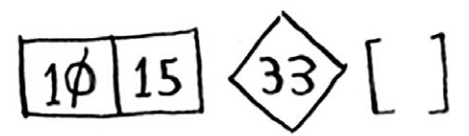
如果子数组是有序的,就可以像下面这样合并得到一个有序的数组:左边的数组 + 基准值 +右边的数组。在这里,就是[10, 15] + [33] + [],结果为有序数组[10, 15, 33]。
如何对子数组进行排序呢?对于包含两个元素的数组(左边的子数组)以及空数组(右边的子数组),快速排序知道如何将它们排序,因此只要对这两个子数组进行快速排序,再合并结果,就能得到一个有序数组!1
2quicksort([15, 10]) + [33] + quicksort([])
> [10, 15, 33] # 一个有序数组
不管将哪个元素用作基准值,这都管用。假设你将15用作基准值。

这个子数组都只有一个元素,而你知道如何对这些数组进行排序。现在你就知道如何对包含三个元素的数组进行排序了,步骤如下。
(1) 选择基准值。
(2) 将数组分成两个子数组:小于基准值的元素和大于基准值的元素。
(3) 对这两个子数组进行快速排序。
包含四个元素的数组呢?

假设你也将33用作基准值。

左边的子数组包含三个元素,而你知道如何对包含三个元素的数组进行排序:对其递归地调用快速排序。

因此你能够对包含四个元素的数组进行排序。如果能够对包含四个元素的数组进行排序,就能对包含五个元素的数组进行排序。为什么呢?假设有下面这样一个包含五个元素的数组。

根据选择的基准值,对这个数组进行分区的各种可能方式如下。

注意,这些子数组包含的元素数都在0~4内,而你已经知道如何使用快速排序对包含0~4个元素的数组进行排序!因此,不管如何选择基准值,你都可对划分得到的两个子数组递归地进行快速排序。
例如,假设你将3用作基准值,可对得到的子数组进行快速排序。
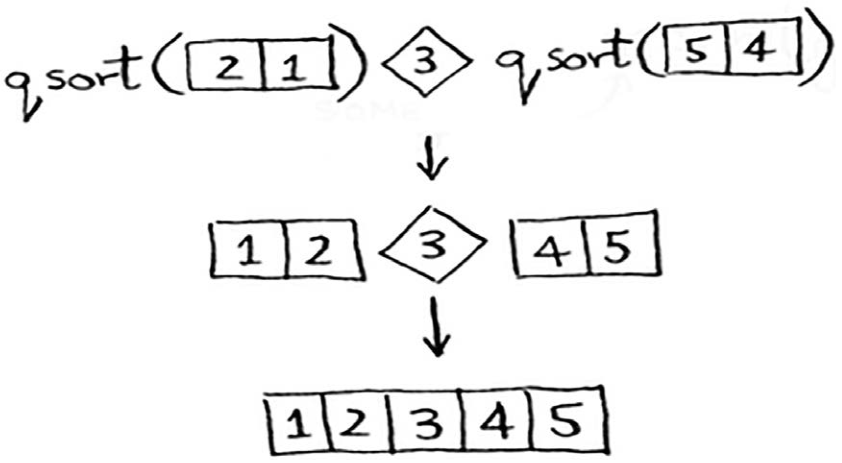
将子数组排序后,将它们合并,得到一个有序数组。即便你将5用作基准值,这也可行。

将任何元素用作基准值都可行,因此你能够对包含五个元素的数组进行排序。同理,你能够对包含六个元素的数组进行排序,以此类推。
归纳证明
刚才你大致见识了归纳证明!归纳证明是一种证明算法行之有效的方式,它分两步:基线条件和归纳条件。是不是有点似曾相识的感觉?例如,假设我要证明我能爬到梯子的最上面。递归条件是这样的:如果我站在一个横档上,就能将脚放到下一个横档上。换言之,如果我站在第二个横档上,就能爬到第三个横档。这就是归纳条件。而基线条件是这样的,即我已经站在第一个横档上。因此,通过每次爬一个横档,我就能爬到梯子最顶端。
对于快速排序,可使用类似的推理。在基线条件中,我证明这种算法对空数组或包含一个元素的数组管用。在归纳条件中,我证明如果快速排序对包含一个元素的数组管用,对包含两个元素的数组也将管用;如果它对包含两个元素的数组管用,对包含三个元素的数组也将管用,以此类推。因此,我可以说,快速排序对任何长度的数组都管用。这里不再深入讨论归纳证明,但它很有趣,并与D&C协同发挥作用。
下面是快速排序的代码。1
2
3
4
5
6
7
8
9
10
11
12def quicksort(array):
if len(array) < 2:
return array # 基线条件:为空或只包含一个元素的数组是“有序”的
else:
pivot = array[0] # 递归条件
less = [i for i in array[1:] if i <= pivot] # 由所有小于基准值的元素组成的子数组
greater = [i for i in array[1:] if i > pivot] # 由所有大于基准值的元素组成的子数组
return quicksort(less) + [pivot] + quicksort(greater)
print quicksort([10, 5, 2, 3])
再谈大O表示法
快速排序的独特之处在于,其速度取决于选择的基准值。在讨论快速排序的运行时间前,我们再来看看最常见的大O运行时间。
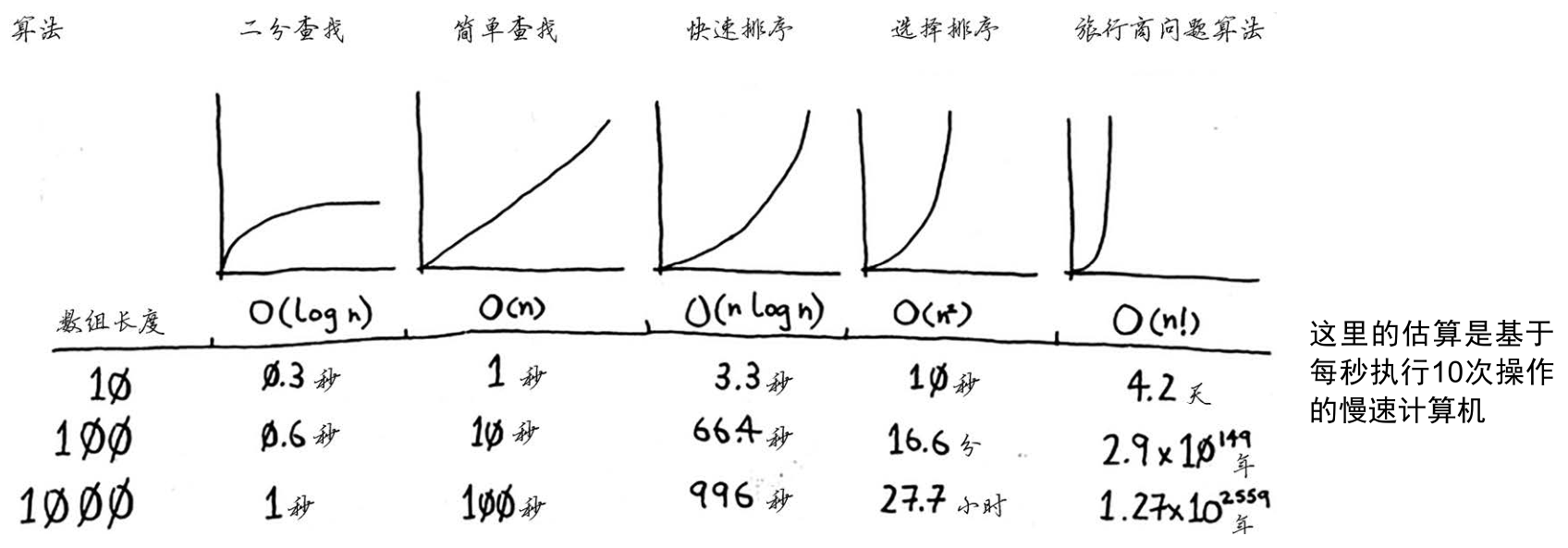
上述图表中的时间是基于每秒执行10次操作计算得到的。这些数据并不准确,这里提供它们只是想让你对这些运行时间的差别有大致认识。实际上,计算机每秒执行的操作远不止10次。
对于每种运行时间,本书还列出了相关的算法。来看看第2章介绍的选择排序,其运行时间为O(n2),速度非常慢。
还有一种名为合并排序(merge sort)的排序算法,其运行时间为O(n log n),比选择排序快得多!快速排序的情况比较棘手,在最糟情况下,其运行时间为O(n2)。
与选择排序一样慢!但这是最糟情况。在平均情况下,快速排序的运行时间为O(n log n)。你可能会有如下疑问。
- 这里说的最糟情况和平均情况是什么意思呢?
- 若快速排序在平均情况下的运行时间为O(n log n),而合并排序的运行时间总是O(n log n),为何不使用合并排序?它不是更快吗?
比较合并排序和快速排序
假设有下面这样打印列表中每个元素的简单函数。1
2
3def print_items(list):
for item in list:
print item
这个函数遍历列表中的每个元素并将其打印出来。它迭代整个列表一次,因此运行时间为O(n)。现在假设你对这个函数进行修改,使其在打印每个元素前都休眠1秒钟。1
2
3
4
5
6from time import sleep
def print_items2(list):
for item in list:
sleep(1)
print item
它在打印每个元素前都暂停1秒钟。假设你使用这两个函数来打印一个包含5个元素的列表。

这两个函数都迭代整个列表一次,因此它们的运行时间都为O(n)。你认为哪个函数的速度更快呢?我认为print_items要快得多,因为它没有在每次打印元素前都暂停1秒钟。因此,虽然使用大O表示法表示时,这两个函数的速度相同,但实际上print_items的速度更快。在大O表示法O(n)中,n实际上指的是这样的。

c是算法所需的固定时间量,被称为常量。例如,print_items所需的时间可能是10毫秒*n,而print_items2所需的时间为1秒*n。
通常不考虑这个常量,因为如果两种算法的大O运行时间不同,这种常量将无关紧要。就拿二分查找和简单查找来举例说明。假设这两种算法的运行时间包含如下常量。
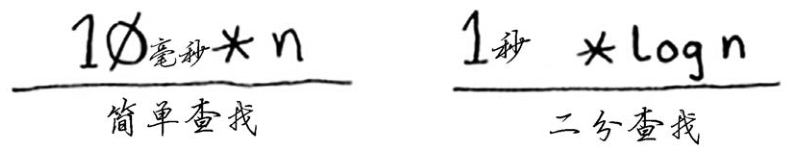
你可能认为,简单查找的常量为10毫秒,而二分查找的常量为1秒,因此简单查找的速度要快得多。现在假设你要在包含40亿个元素的列表中查找,所需时间将如下。

正如你看到的,二分查找的速度还是快得多,常量根本没有什么影响。
但有时候,常量的影响可能很大,对快速查找和合并查找来说就是如此。快速查找的常量比合并查找小,因此如果它们的运行时间都为O(n log n),快速查找的速度将更快。实际上,快速查找的速度确实更快,因为相对于遇上最糟情况,它遇上平均情况的可能性要大得多。
此时你可能会问,何为平均情况,何为最糟情况呢?
平均情况和最糟情况
快速排序的性能高度依赖于你选择的基准值。假设你总是将第一个元素用作基准值,且要处理的数组是有序的。由于快速排序算法不检查输入数组是否有序,因此它依然尝试对其进行排序。

注意,数组并没有被分成两半,相反,其中一个子数组始终为空,这导致调用栈非常长。现在假设你总是将中间的元素用作基准值,在这种情况下,调用栈如下。
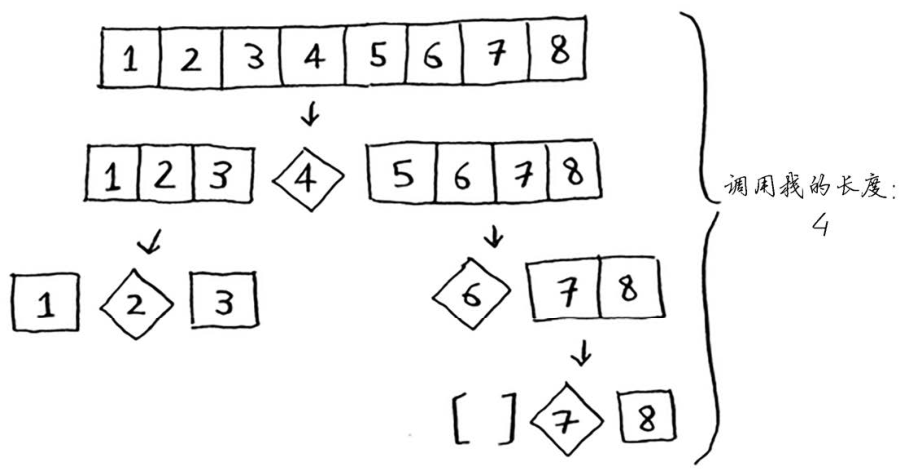
调用栈短得多!因为你每次都将数组分成两半,所以不需要那么多递归调用。你很快就到达了基线条件,因此调用栈短得多。
第一个示例展示的是最糟情况,而第二个示例展示的是最佳情况。在最糟情况下,栈长为O(n),而在最佳情况下,栈长为O(log n)。
现在来看看栈的第一层。你将一个元素用作基准值,并将其他的元素划分到两个子数组中。这涉及数组中的全部8个元素,因此该操作的时间为O(n)。在调用栈的第一层,涉及全部8个元素,但实际上,在调用栈的每层都涉及O(n)个元素。

即便以不同的方式划分数组,每次也将涉及O(n)个元素。

因此,完成每层所需的时间都为O(n)。

在这个示例中,层数为O(log n)(用技术术语说,调用栈的高度为O(log n)),而每层需要的时间为O(n)。因此整个算法需要的时间为O(n) * O(log n) = O(n log n)。这就是最佳情况。
在最糟情况下,有O(n)层,因此该算法的运行时间为O(n) * O(n) = O(n2)。
知道吗?这里要告诉你的是,最佳情况也是平均情况。只要你每次都随机地选择一个数组元素作为基准值,快速排序的平均运行时间就将为O(n log n)。快速排序是最快的排序算法之一,也是D&C典范。
练习
5.使用大O表示法时,下面各种操作都需要多长时间?
6.打印数组中每个元素的值。
7.将数组中每个元素的值都乘以2。
8.只将数组中第一个元素的值乘以2。
9.根据数组包含的元素创建一个乘法表,即如果数组为[2, 3, 7, 8, 10],首先将每个元素都乘以2,再将每个元素都乘以3,然后将每个元素都乘以7,以此类推。
小结
- D&C将问题逐步分解。使用D&C处理列表时,基线条件很可能是空数组或只包含一个元素的数组。
- 实现快速排序时,请随机地选择用作基准值的元素。快速排序的平均运行时间为O(n log n)。
- 大O表示法中的常量有时候事关重大,这就是快速排序比合并排序快的原因所在。
- 比较简单查找和二分查找时,常量几乎无关紧要,因为列表很长时,O(log n)的速度比O(n)快得多。
答案
4.11
2
3
4def sum(list):
if list == []:
return 0
return list[0] + sum(list[1:])
4.21
2
3
4def count(list):
if list == []:
return 0
return 1 + count(list[1:])
4.31
2
3
4
5def max(list):
if len(list) == 2:
return list[0] if list[0] > list[1] else list[1]
sub_max = max(list[1:])
return list[0] if list[0] > sub_max else sub_max
4.4 二分查找的基线条件是数组只包含一个元素。如果要查找的值与这个元素相同,就找到了!否则,就说明它不在数组中。
在二分查找的递归条件中,你把数组分成两半,将其中一半丢弃,并对另一半执行二分查找。
4.5 O(n)。
4.6 O(n)。
4.7 O(1)。
4.8 O(n2)。